A continuación se plantea un problema de disfraces que da lugar a un sistema de dos ecuaciones lineales, el cual se resuelve primero de manera gráfica y después de manera algebraica, para observar la relación entre estos dos procedimientos se facilita su comprensión con un esquema de cuatro pasos que se conoce como Método de suma o resta, a continuación revísalo.
Todos los alumnos del grupo 0141 del CCH se preparan para ir a una fiesta de disfraces. El disfraz para cada hombre cuesta 60 pesos y el disfraz para cada mujer cuesta 90 pesos. Si en el grupo hay 45 alumnos entre hombres y mujeres, y pagan 3,300 pesos por todos los disfraces ¿cuántos hombres y cuántas mujeres van a la fiesta?

| Si representamos por: | Se tiene lo siguiente: |
|---|---|
|
x: el número mujeres. y: el número de hombres. |
90x es la cantidad de dinero en pesos que se paga por los disfraces de las mujeres. 60y es la cantidad de dinero en pesos que se paga por los disfraces de los hombres. |
El sistema de ecuaciones que cumple las condiciones del problema y cuya solución nos lleva a resolverlo es:
x+y=45 Ec. 1
90x+60y=3300 Ec. 2
La solución del sistema está dada por la solución común de las dos ecuaciones, es decir, los valores de x, y que cumplen con las dos ecuaciones a la vez.
Esta solución del sistema se obtiene de las gráficas de las ecuaciones construidas en un mismo plano cartesiano. Por medio de una tabulación para cada una de las ecuaciones, se obtienen las coordenadas de los puntos a partir de los cuales se construye la gráfica respectiva. Es importante señalar que las coordenadas (x, y) de cada punto representan una solución de la ecuación correspondiente.
Para hacer una tabulación se puede despejar y de la ecuación, sustituir en ella los valores de x que se deseen para obtener los puntos (x, y) que cumplen la ecuación y graficar éstos en un sistema cartesiano, como se mostrará posteriormente.
La solución del sistema está dada por la solución común de las dos ecuaciones: los mismos valores de x, y que cumplen con las dos ecuaciones a la vez. Las coordenadas del punto de intersección de las gráficas resultante es la solución del sistema.
A continuación revisa cada uno de los pasos de esta solución gráfica dando clic en las pestaña.
Tabulación de la ecuación Ec. 1
De la Ec. 1 se despeja y:
x+y=45 Ec. 1
x+y−x=45−x
y=45−x Ec. 1'
Por lo que los puntos que cumplen la condición de la ecuación Ec. 1' se expresan como:
A=(x,y)=(x,45−x)
Para saber los valores de y=45−x, se sustituye el valor de x como se muestra a continuación:
x=0,y=45−x=45−0=45 Se obtiene el punto (0,45)
x=10,y=45−10=35 Se obtiene el punto (10,35)
x=20,y=45−20=25 Se obtiene el punto (20,25), etc.
Practicando
De esta manera se obtiene la siguiente tabla, obsérvala y completa los valores y puntos que faltan. Al finalizar da clic en Verificar para recibir retroalimentación.
Tabulación de la ecuación Ec.2
De la Ec. 2 se despeja y:
90x+60y=3300 Ec. 2
90x+60y−90x=3300−90x (se resta 90x a los dos lados de la ecuación)
60y=3300−90x (se simplifica)
60y60=3300−90x60 (se divide entre 60 los dos lados de la ecuación)
Ec. '2 y=55−1.5x (se simplifica 3300−90x60=330060=90x60x=55−1.5x)
Por lo que los puntos que cumplen la condición de la ecuación Ec.2 se expresan como:
B=(x,y)=(x,55−1.5x)
Para x=0, y=55−1.5(0)=55−0=55 Se obtiene el punto (0,55)
x=10, y=55−1.5(10)=55−15=40 Se obtiene el punto (10,40)
x=20, y=55−1.5(20)=55−30=25 Se obtiene el punto (20,25), etc.
Practicando
De esta manera se obtiene la tabla 2, obsérvala y completa los valores y puntos que faltan. Al finalizar da clic en Verificar para recibir retroalimentación.
Solución gráfica del sistema
A continuación revisa el siguiente recurso GeoGebra sobre la Solución gráfica del problema de disfraces en el que observarás las diferentes coordenadas de los puntos A y B que cumplen con cada una de las ecuaciones del sistema, así como el punto de intersección de las gráficas para dar con la solución.
Observa que solo la parte continua de las rectas tiene sentido en el problema, ya que tanto x: el número mujeres que van a la fiesta como y: el número de hombres que van a la fiesta deben ser ambos positivos.
Solución y comprobación del problema
Finalmente se da la respuesta al problema que se propuso resolver, utilizando la solución gráfica del sistema con el significado que se dio a las incógnitas y al comprobar que el problema mismo se resolvió correctamente:
x: el número de mujeres que van a la fiesta
y: el número de hombres que van a la fiesta
La solución gráfica del sistema de la ecuación es: x=20, y=25
20 mujeres y 25 hombres que van a la fiesta
Comprobación del problema:
Se verifica que la respuesta dada cumpla con las condiciones del problema, porque puede suceder que se resuelvan las ecuaciones muy bien pero el problema no, por algún error que se haya cometido en el planteamiento.
20+25=45 Se cumple que son 45 alumnos en el grupo.
90(20)+60(25)=1800+1500=3300 Se cumple que se paga 3300 pesos por todos los disfraces.
Por lo que se concluye que la respuesta dada al problema es correcta.
Ahora revisarás la solución del sistema de ecuaciones del problema de disfraces de manera algebraica por el Método de Suma o Resta.
x+y=45 Ec. 1
90x+60y=3300 Ec. 2
La solución del sistema está dada por la solución común de las dos ecuaciones, es decir, los mismos valores de x e y que cumplan con las dos ecuaciones a la vez.
Para determinar la solución del sistema por el Método de Suma o Resta seguirás estos cuatro pasos, da clic en cada pestaña:
Multiplicación de cada ecuación
Se debe multiplicar cada ecuación por números que igualen los coeficientes de una misma incógnita en las dos ecuaciones para eliminar una de las incógnitas. Al hacer esto se obtienen ecuaciones equivalentes a las originales que, al sumarlas o restarlas, conllevan la eliminación de esa incógnita y se obtiene una ecuación con la otra incógnita solamente.
Una forma de lograr esto, para igualar los coeficientes de y, es multiplicar la Ec. 1 por el coeficiente 60 de y de la Ec.2 y multiplicar la Ec.2 por el coeficiente 1 de y de la Ec.1 como se hace a continuación:
De la Ec.1 60(x+y=45) se obtiene 60x+60y=2700 Ec.1’
De la Ec.2 1(90x+60y=3300) se obtiene 90x+60y=3300 Ec.2’

Sumar o restar las ecuaciones
Se suman o se restan las ecuaciones Ec.1’ y Ec.2’ para eliminar una de las incógnitas. En este caso se restan algebraicamente para eliminar la incógnita y, con lo que se obtiene una ecuación con solamente la otra incógnita Ec.3 y se resuelve:
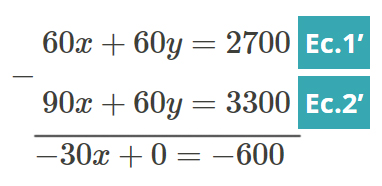
-30x=-600 Ec.3
\frac{-30x}{-30}=\frac{-600}{-30} (se divide entre -30 ambos lados)
x=20 (se simplifica)
Sustituir valores
Se sustituye el valor encontrado x=20 en cualquiera de las ecuaciones que tiene las dos incógnitas, para encontrar el valor de la otra incógnita.
| Sustituyendo en x=20 Ec. 1 | Sustituyendo en x=20 Ec. 2 |
|---|---|
|
x+y=45 20+y=45 20+y-20=45-20 y=25 |
90x+60y=3300 90(20)+60y=3300 1800+60y=3300 1800+60y-1800=3300-1800 60y=1500 \frac{60y}{60}=\frac{1500}{60} y=25 Observa que se obtiene el mismo valor que en Ec. 1 |
Comprobación
Sustituye la solución encontrada x=20, y=25 en cada una de las dos ecuaciones originales para verificar que se cumpla la igualdad.



