La intención de este material es que reconozcas en las Matemáticas actividades que realizas cotidianamente, y que a partir de cierto número de observaciones y datos puedas construir un Modelo matemático . Se espera que con los diversos problemas que se presentan reconozcas patrones numéricos y geométricos empleando estrategias heurísticas, las cuales te permitirán modelar su comportamiento a través de fórmulas. Las estrategias heurísticas son reglas muy generales que te permiten transformar un problema en una situación sencilla. Así la capacidad heurística es un rasgo que caracteriza a los humanos y se puede describir como el arte y la ciencia del descubrimiento y de la capacidad de resolver problemas mediante la creatividad.
Un personaje que mostró tener capacidad heurística fue el matemático, físico y astrónomo alemán Carl Friedrik Gauss (1777-1855); nació en el seno de una familia humilde, hijo de un albañil, desde muy temprana edad dio muestras de una prodigiosa capacidad para las Matemáticas.
A los nueve años, su maestro de escuela, que quería paz en la clase, solicitó a los niños que sumaran todos los números comprendidos entre 1 y 100, pensando que con este problema la clase estaría ocupada, sin embargo, casi inmediatamente, Gauss escribió en su pizarra: 5050; ante los ojos atónitos del profesor y sus compañeros.
Probablemente Gauss intuitivamente se dio cuenta de que, la suma de la primera y la última cifra daba el mismo resultado que la suma de la segunda y penúltima cifra y así sucesivamente, es decir:
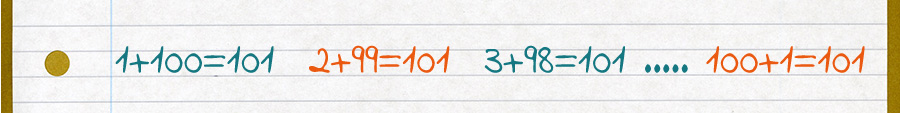

Carl Friedrik. Christian Albrecht Jensen
Como hay 50 parejas de números, el resultado se obtiene:
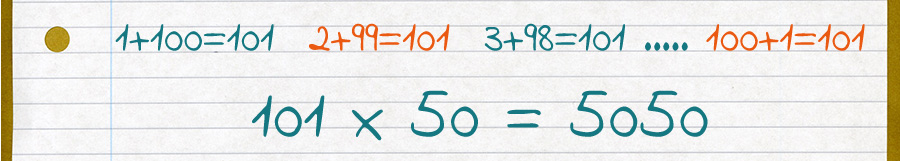
Ahora se espera que igual que Gauss, utilices tu intuición para reconocer patrones numéricos y geométricos de algunas situaciones problemáticas como las siguientes:

Con este material reconocerás patrones numéricos y geométricos de algunas situaciones problemáticas y expresarás simbólicamente generalizaciones de estas situaciones, mediante el empleo de estrategias heurísticas para modelar su comportamiento a través de fórmulas.


