Un número b es divisible entre un número a si existe un número c, tal que b=a∙c, es decir, la división es exacta ab=c; dicho de otro modo, el residuo de la división es cero. Por ejemplo, el número 24 es divisible por 8, puesto que existe el número 3, tal que 24=8∙3, es decir, la división es exacta 248=3; en cambio, el número 36 no es divisible por 5, puesto que no existe un número entero c, cuyo producto sea 36=5∙c.

A continuación se presentan unos conceptos que ayudan a comprender la divisibilidad de los numeros naturales. Da clic en cada una de las pestañas para que puedas revisar la información.
Son aquellos que tienen dos divisores, uno de ellos es el mismo número y el otro es el número 1. Por ejemplo, el número 13 tiene como divisores sólo a los números 13 y 1, luego es un número primo; por el contrario el 24 no es número primo ya que tiene como divisores a los números 1,2,3,4,6,8,12 y 24. A los números que tienen más de dos divisores se les llama números compuestos. Cabe mencionar que el número 1 no es número primo ni compuesto, puesto que su único divisor es el mismo 1. Los primeros números primos comprendidos entre los primeros 50 números naturales son 2,3,5,7,11,13,17,19,23,29,31,37,41,43 y 47.
Es el mayor de los divisores (factores) en común de dos números naturales o más. Para obtener el MCD de dos o más números se tienen dos procedimientos. El primero consiste en obtener los divisores de cada uno de los números y se toma el mayor; el otro procedimiento requiere descomponer a cada uno de los números en sus factores primos, el producto de los factores primos (fp) en común es el MCD.
Por ejemplo obtener el MCD (12,18,24) con los procedimientos mencionados.
Primer procedimiento
Éste refiere a la enumeración de los divisores (factores) de los números 12,18 y 24. El mayor de éstos es el máximo común divisor, tal como se ejemplifica en la tabla.
Segundo procedimiento
Consiste en dividir a los números 12, 18 y 24 por sus factores primos, empezando por el 2 y colocando los cocientes en el renglón correspondiente de la tabla, se repite el proceso hasta que los números ya no sean divisibles por 2, si los números del último renglón son unos el proceso termina, sino se considera el siguiente factor primo (3) y se dividen los números entre éste hasta que ya no sean divisibles por 3. En caso de que los cocientes del último renglón sean unos, el proceso termina, sino el proceso se repite para los siguientes factores primos. El producto de los factores primos (números en color azul de la tabla) es el máximo común divisor, tal como se aprecia a continuación.
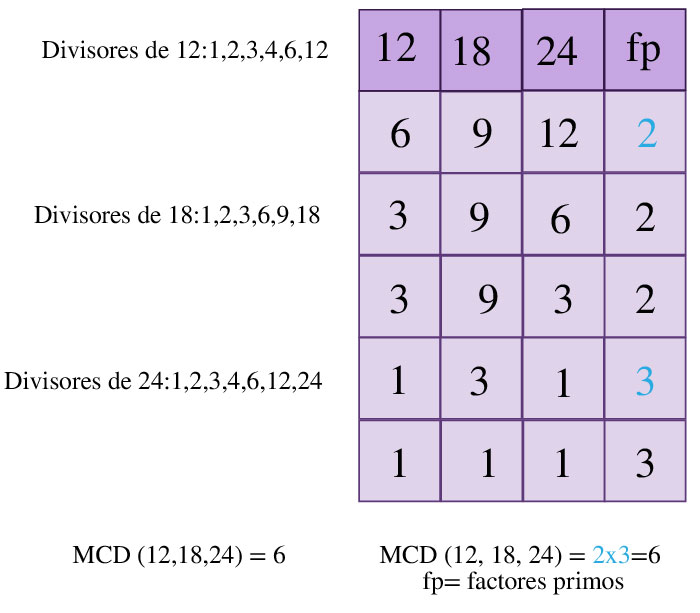
En ambos casos el MCD (12,18,24)=6, puesto que 6 es el mayor divisor común de los números 12,18 y 24, asimismo, el producto de sus factores primos en común es 6.
Es el menor de todos los múltiplos comunes de dos números naturales o más. Para obtener el mcm de dos o más números se tienen dos procedimientos. El primero consiste en obtener los múltiplos de cada uno de los números y se toma el menor; el segundo procedimiento implica descomponer a cada uno de los números en sus factores primos, tal como se explicó en el segundo procedimiento para obtener el MCD. El producto de los factores primos es el mcm, esto puedes obsérvalo en la siguiente tabla.
Por ejemplo obtener el mcm (3,5,6) con los procedimientos mencionados.
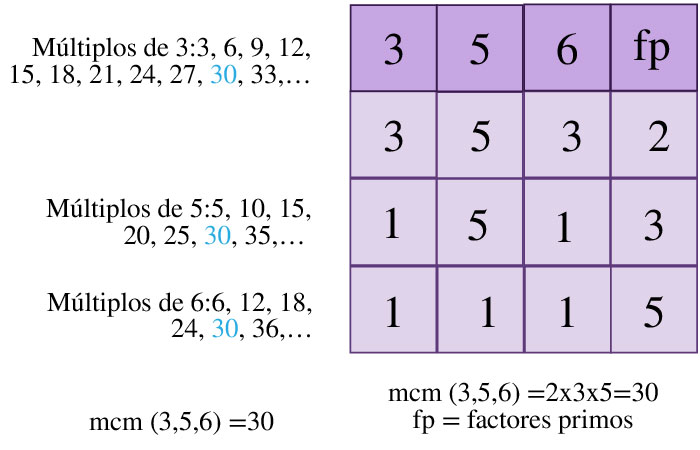
En ambos casos el mcm (3,5,6)=30, puesto que 30 es el menor de los múltiplos comunes de los números 3,5 y 6; por otro lado, el producto de sus factores primos es 30=2•3•5.
Es importante que recuerdes y comprendas las propiedades de los números reales, en particular para los números enteros que se especifican en la tabla.
| Para los números enteros a, b y c | Adición | Multiplicación |
Propiedad conmutativa |
a+b=b+a | ab=ba |
Propiedad asociativa |
(a+b)+c=a+ (b+c) | (ab)c=a(bc) |
Neutros, aditivo (0) y multiplicativo (1) |
0+a=a+0=a | 1∗a=a∗1=a |
Inverso aditivo y multiplicativo |
a+(−a)=−a+a=0 | a(1a)=1a(a)=1 |
Propiedad distributiva de la multiplicación, respecto a la adición |
a(b+c)=ab+ac a(b+c)=ab+ac |
|


