d. Obtención de la función lineal a partir de la gráfica (dos puntos)
Como parte de la comprensión del concepto de la función lineal, es necesario obtener el proceso inverso a la descripción de la gráfica a partir de sus parámetros; es decir, dados dos puntos de la gráfica, es posible determinar la función lineal asociada.
Practicando
¿Te acuerdas del Problema de la caminadora? Al iniciar (t=0) la atleta no ha recorrido ninguna distancia (d=0). Pero al terminar su entrenamiento en t=40 minutos ha recorrido una distancia d=8 Km. Utilicemos estos dos puntos de referencia para determinar la función lineal asociada y=mx+b, en ésta sólo falta determinar el valor de la razón de cambio m (rapidez de cambio).
¿Te acuerdas del Problema del celular? Cuando no se ha hablado nada en el tiempo inicial (t=0) no ha generado ningún costo (c=0). Después de hablar 25 minutos (t=25), se agota un saldo de $50 (c=50). Utilicemos estos dos puntos de referencia para determinar la ecuación asociada.
Con el siguiente ejercicio determinarás la función lineal que se presenta en la gráfica, mediante el cociente de la variación del cambio de la variable dependiente entre el cambio de la variable independiente, para que obtengas la función lineal al sustituir la razón de cambio en ésta.
Observa la gráfica y considera los datos que contiene para completar los espacios correspondientes de la tabla. Al finalizar, da clic en Verificar para recibir retroalimentación.
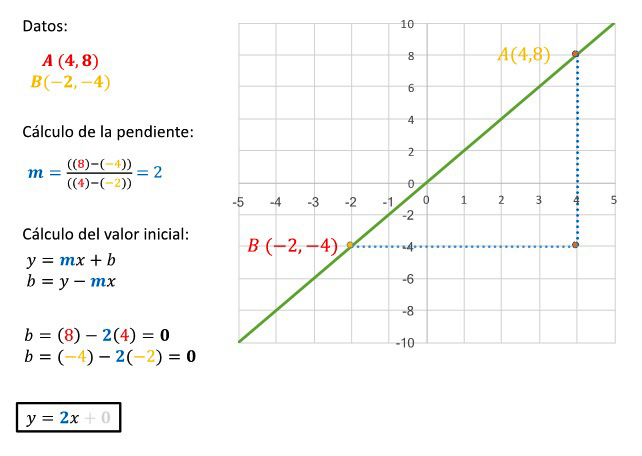
Considera
Ahora verás el procedimiento para determinar la función y=ax+b, considerando las coordenadas de los puntos A(x1,y1) y B(x2,y2):
- Identificar dos puntos A(x1,y1) y B(x2,y2).
- Obtener la razón de cambio m=(y1−y2)(x1−x2)
- Obtener la ordenada al origen, despejar desde y=mx+b: b=y−mx
Como los puntos A(x1,y1) y B(x2,y2) pertenecen a la gráfica de la función y al sustituir sus coordenadas en la ordenada al origen se obtiene: b=y1−mx1 b=y2−mx2 - Para cualquier punto la ecuación queda como: y=mx+b
A continuación, contesta las preguntas, al finalizar da clic en el botón Verificar para recibir retroalimentación.
Entra al recurso GeoGebra PENDIENTE 08 y sigue las instrucciones. A través del escenario interactivo podrás revisar el procedimiento de cálculo de la función lineal a partir de dos puntos de la gráfica, para ello, determina las formas de la función lineal vistas previamente, es decir, trata de generar razones de cambio positivas y negativas (m también conocidas como parámetro lineal, tienen una “pendiente” o dirección de la gráfica ascendente y descendente dependiendo del signo) de la gráfica.
Te resultará de ayuda responder cuestionamientos como ¿qué sucede cuando los puntos están próximos en los ejes x o y?, considerando que éstos determinen si la gráfica pasa por el origen (función lineal) o se desplaza dentro del escenario. Al finalizar, deberás lograr una intuición sobre las formas de gráficas que se generan cuando varían los parámetros de la razón de cambio (m) y de la condición inicial (b).
Practicando
Con el siguiente ejercicio profundizarás en los procedimientos algebraicos realizados para determinar la función lineal, mediante tu interacción y exploración de los procesos presentados en el recurso GeoGebra en la obtención de la razón de cambio y la función lineal, para que la apliques en la resolución de problemas que involucran a la función lineal.
A partir de los siguientes puntos, determina cuál es la expresión algebraica de la función lineal. Da clic en las pestañas y sigue las instrucciones, puedes auxiliarte del recurso interactivo de GeoGebra anterior. Al finalizar da clic en Verificar para recibir retroalimentación.



