1. Inicio
  2. Matemáticas 1
  3. Unidad 4
  4. Método de sustitución
  5. S. compatible con infinidad...

S. compatible con infinidad...

Sistema compatible con infinidad de soluciones

A continuación, se resuelve el siguiente sistema de ecuaciones por el método de sustitución siguiendo los mismos pasos que en el Problema de las monedas.

$x+3y=4$       Ec. 1

$2x+6y=8$       Ec. 2

Practicando

Revisa los diferentes pasos para encontrar la solución del sistema dando clic en cada una de las pestañas. Sigue las indicaciones y contesta lo que se pide en los espacios correspondientes. Al finalizar da clic en Verificar para recibir retroalimentación.

Se despeja la incógnita $y$ de cualquiera de las dos ecuaciones

Esto se hace para encontrar la representación algebraica de los puntos que representan la solución de una de las ecuaciones. Se escoge despejar de la ecuación Ec. 1, y se obtiene Ec. 1’:

Completa todas tus respuestas para recibir retroalimentación.
$x+3y=4$ Ec. 1

$x+3y-$ $x$$=4-$ $x$

$3y$$=4-x$

$3y$
$=$
$4-x$
$\frac{3y}{3}=\frac{4-x}{3}$

$y=$
$4-x$
    Ec. 1’ $y=\frac{4-x}{3}$

Por tanto, los puntos que cumplen la condición de la ecuación Ec. 1 son:

$A=(x,y)=(x,\frac{4 -x}{3})$

Si tus respuestas son correctas has comprendido el proceso para despejar adecuadamente la incógnita solicitada del sistema de ecuaciones, en caso contrario, revisa nuevamente el contenido para aclarar dudas.

Se sustituye $y$ de la ecuación Ec.1’ en la ecuación Ec.2 del sistema

Para que los puntos $A=(x,y)=\left ( x,\frac{4 -x}{3} \right )$ que cumplen con la ecuación Ec.1 cumplan también con la otra ecuación Ec.2, se requiere que sus valores $(x,y)$ sean los mismos, por lo que Ec.1’ $y=\frac{4 -x}{3}$ se sustituye en la ecuación Ec.2 $2x+6y=8$, y se resuelve la ecuación resultante de una sola incógnita para obtener su valor, como se muestra a continuación:

Completa todas tus respuestas para recibir retroalimentación.
$2x+6y=8$         Ec. 2

$2x+$ $6$$(\frac{4-x}{3})=$ $8$ Ec. 3

(se sustituye $y$ de Ec.1’)
$2x+$
$24-$
$3$
$=8$ $2x+(\frac{24-6x}{3})=8$

(ya que $6\left ( \frac{4-x}{3} \right )=\frac{24-6x}{3}$)

$2x+8-2x=8$

(ya que $\frac{24-6x}{3}=8-2x$)

$8$$=8$

(se simplifica)

Si tus respuestas son correctas has comprendido el proceso para sustituir incógnitas en un sistema de ecuaciones, en caso contrario, revisa nuevamente el contenido para aclarar dudas.

Observa que no aparece $x$ en la ecuación, pero sí se cumple que $8=8$. Esto significa que para cualquier valor que tenga la incógnita $x$ en la ecuación 1 o en la ecuación 2, se cumplirá siempre la ecuación Ec. 3, por lo que el sistema tiene infinidad de soluciones como se verá a continuación.

Se sustituye el valor encontrado

En este caso el valor de $x$ que se quiera, en cualquiera de las ecuaciones que tenga ambas incógnitas, para encontrar el valor de la otra incógnita. Se escoge sustituir en Ec. 1’:

Completa todas tus respuestas para recibir retroalimentación.
Sustituyendo $x=7$ en Ec. 1 Sustituyendo $y=2$ en Ec. 2

$x+3y=4$ en Ec. 1

$2x+6y=8$ en Ec. 2

$7$$+3y=4$

$2x+6($ $2$$)=8$

$7+3y-$ $7$$=4-7$

$2x+$ $12$$=8$

$3y$$=-3$

$2x+12-12=8-$ $12$
$3y$
$=\frac{-3}{3}$ $\frac{3y}{3}=\frac{-3}{3}$

$2x$$=-4$

$y=-1$
$\frac{2x}{2}=$
$-4$
$\frac{2x}{2}=\frac{-4}{2}$

$x=-2$

Por tanto, una solución es $x=7$, $y=-1$

Por tanto, otra solución es $x=$ $-2$, $y=2$

Si tus respuestas son correctas has comprendido el proceso para sustituir valores de incógnitas en un sistema de ecuaciones, en caso contrario, revisa nuevamente el contenido para aclarar dudas.

De esta manera se pueden generar infinidad de soluciones.

Sustituyendo $x=7$ en Ec. 2 Sustituyendo $y=2$ en Ec. 1

$2x+6y=8$

$x+3y=4$

$2(7)+6y=8$

$x+3(2)=4$

$14+6y=8$

$14+6y-14=8-14$

$x+6=4$

$6y=-6$

$x+6-6=4-6$

$\frac{6y}{6}=\frac{-6}{6}$

$x=-2$

$y=-1$

Observa que se obtiene el mismo valor que en Ec. 1

Observa que también se obtiene el mismo valor que en Ec. 2

Comprobación

Se sustituyen la solución encontrada en cada una de las ecuaciones originales para verificar que se cumplan.

Completa todas tus respuestas para recibir retroalimentación.

Para $x=7$, $y=-1$

$x+3y=4$ Ec. 1

$7+3($ $-1$$)=4$

$7-$ $3$$=4$

$4=4$

$2x+6y=8$ Ec. 2

$2($ $7$$)+6($ $-1$$)=8$

$14-$ $6$$=8$

$8$$=8$

Como las dos ecuaciones se cumplen con $x=7$, $y=$ $-1$, la solución del sistema es correcta.

Para $x=-2$, $y=2$

$x+3y=4$ Ec. 1

$-2+3($ $2$$)=4$

$-2$$+6=4$

$4=4$

$2x+6y=8$ Ec. 2

$2($ $-2$$)+6($ $2$$)=8$

$-4$$+12=8$

$8$$=8$

Como las dos ecuaciones se cumplen con $x=-2$, $y=$ $2$, la solución del sistema es correcta.

Si tus respuestas son correctas has comprendido el proceso de comprobación para la solución encontrada en un sistema de ecuaciones, en caso contrario, revisa nuevamente el contenido para aclarar dudas.

De la misma manera se puede comprobar que cualquier solución que cumpla con la Ec. 1 también cumple con la Ec. 2, y viceversa, como se ve a continuación:

Si se multiplican ambos lados de la ecuación Ec. 1 $x+3y=4$ por $2$ para conservar la igualdad, $2(x+3y)=2(4)$, se obtiene la ecuación equivalente a Ec. 1: $2x+6y=$$8$; mientras que la condición de la ecuación de la Ec. 2 es también $2x+6y=$$8$, por lo que cualquier punto ($x,y$) que cumple con la Ec. 1 también cumple con la Ec. 2, y viceversa, ya que $2x+6y$ tiene el mismo valor $8$ en las dos ecuaciones a la vez.

Por lo que se concluye que todas las soluciones de la ecuación Ec. 1 también son soluciones de la ecuación Ec. 2, y viceversa.

Este sistema de ecuaciones lineales es, por tanto, un sistema compatible con infinidad de soluciones.

geogebra

A continuación, revisa el recurso GeoGebra Sistema compatible con infinidad de soluciones y sigue las instrucciones.

Observa que en el escenario del recurso GeoGebra las gráficas de las dos ecuaciones coinciden, por lo que se intersectan en todos sus puntos y se tiene infinidad de soluciones. Por lo anterior, este sistema es compatible con infinidad de soluciones.

Observa también que en el sistema 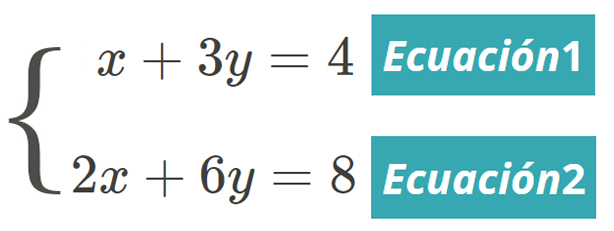ecuaciones la ecuación 2 equivale a la ecuación 1 multiplicada por 2, por lo que todas las soluciones de la ecuación 1 también son soluciones de la ecuación 2 y viceversa, por tanto, se tienen infinidad de soluciones como ya se indicó.