Relaciones de igualdad y orden
En general, dados dos números racionales cualesquiera, $\frac{a}{b}$ y $\frac{c}{d}$, se tienen tres posibles casos de ordenación (tricotomía):
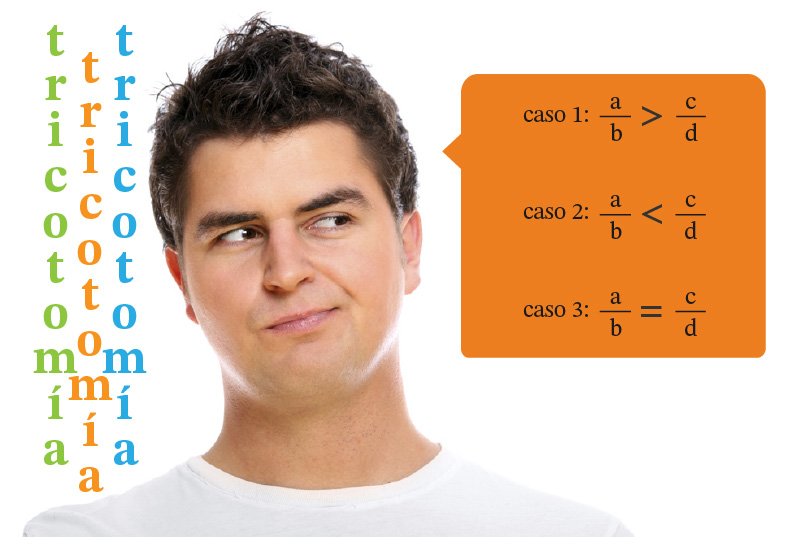
La ubicación de los números en la recta numérica te permite compararlos y determinar el orden entre ellos.
A continuación, se hará un análisis gráfico de los tres casos de ordenación o tricotomía.
Caso 1: $\frac{a}{b} > \frac{c}{d}$
El número racional $\frac{a}{b}$ representa una magnitud mayor que el número $\frac{c}{d}$, por lo que el primer número se ubica a la derecha del segundo.
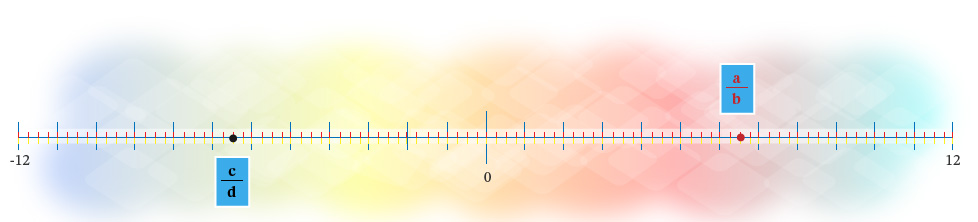
Caso 2: $\frac{a}{b} < \frac{c}{d}$
El número racional $\frac{a}{b}$ representa una magnitud menor que el número $\frac{c}{d}$, por lo que el primer número se ubica a la izquierda del segundo.
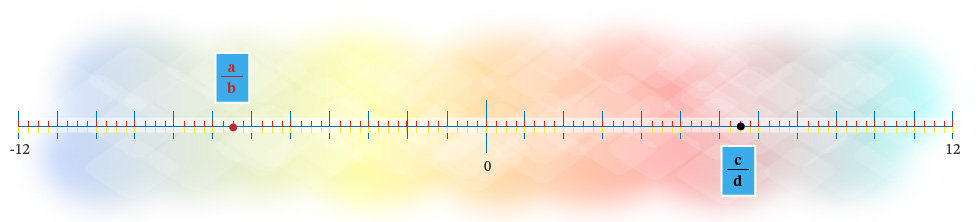
Caso 3: $\frac{a}{b} = \frac{c}{d}$
Ambos números racionales representan a la misma magnitud, por lo que se ubican en la misma posición en la recta numérica. Se dice que las fracciones son equivalentes.
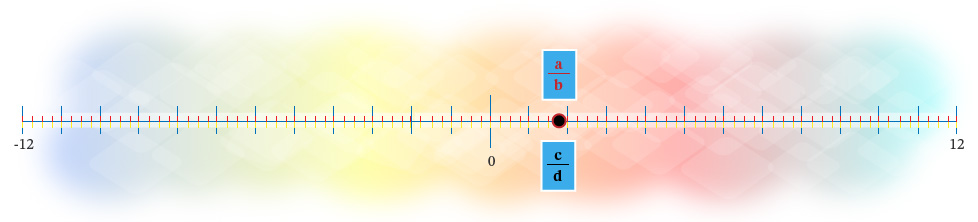
Aunque la localización de números racionales en la recta numérica es un proceso útil para su comparación, dicho proceso puede ser lento y poco práctico, por lo que es conveniente realizar la comparación de manera aritmética.
En la siguiente sección aprenderás a comparar números racionales mediante procesos aritméticos.


