Relación de orden en los números racionales
Al igual que los números enteros, los números racionales también pueden ser localizados en la recta numérica para su ordenación. Por ejemplo, en la figura 5 se muestran los números racionales $\frac{1}{8}$ y $\frac{5}{8}$.
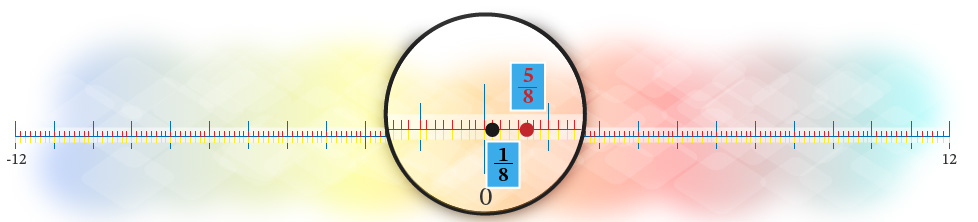
Figura 5. Comparación entre números racionales positivos
Se observa que el número $\frac{1}{8}$ se encuentra a la izquierda de $\frac{5}{8}$, por lo que $\frac{1}{8}$ es menor que $\frac{5}{8}$, es decir:
$\frac{1}{8} < \frac{5}{8}$
En la figura 6 se muestra la relación de orden entre los números $\frac{1}{8}$ y $\frac{5}{8}$

Figura 6.Relación de orden entre los números positivos

Utiliza el siguiente recurso GeoGebra para comparar diferentes números racionales. Para ello modifica los valores del numerador y del denominador, observa su representación en la recta numérica y compáralos. Hazlo seleccionando:
- Números positivos
- Números negativos
- Un número positivo y otro negativo.
Observa que su posición en la recta numérica determina la relación de orden entre los números, tal como ya analizamos con anterioridad. Un número es menor si se encuentra a la izquierda de un segundo número; será mayor si se encuentra a la derecha; y ambos números serán iguales si ocupan el mismo lugar en la recta numérica.



