Son ordenaciones de números naturales sucesivos en celdas que forman un cuadrado, tal que la suma de cualquier fila, columna o diagonal es la misma. El siguiente arreglo cuadrangular es un cuadrado mágico de tamaño $3x3$, puesto que se forma con tres renglones y tres columnas.

Con base en el cuadrado mágico se observa que cada casilla contiene un número natural y la suma de diagonales, renglones y columnas suman $15$, ¿por qué?
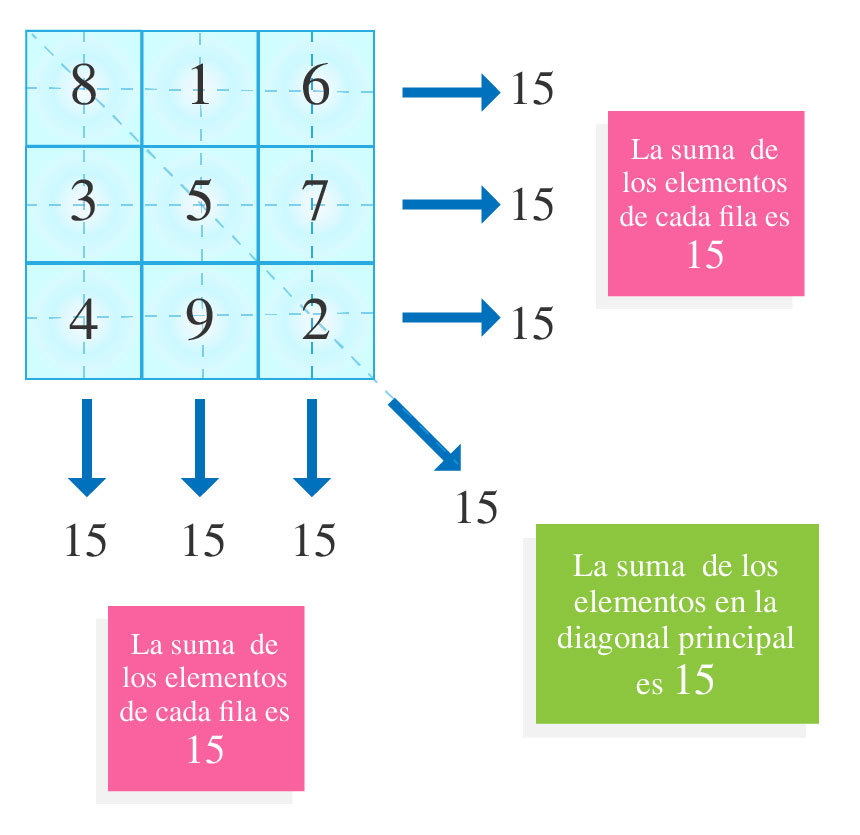
Para contestar la pregunta hagamos la adición de los números que constituyen al cuadro mágico, mismo que se forma con los primeros nueve números naturales $1, 2, 3, 4, 5, 6, 7, 8 $ y $9$; el valor de la suma es $45$, es decir:
$S_9=1+2+3+4+5+6+7+8+9=45$, donde $S_9$ representa la suma de los primeros nueve números naturales. Para calcular la suma de las diagonales del cuadro mágico, $\ S_9$ se divide entre tres (ya que se tienen tres cuadros por diagonal, así como en renglones y columnas), obteniéndose
$S_D=\frac{S_9}{N}=\frac{45}{3}=15$
donde $N$ es el número de cuadros por diagonal y $S_D$ es la suma de los números naturales contenidos en los cuadros de cada diagonal principal. Recuerda la suma de los cuadros en las diagonales es igual a la suma de los cuadros de cada fila, así como de cada columna.
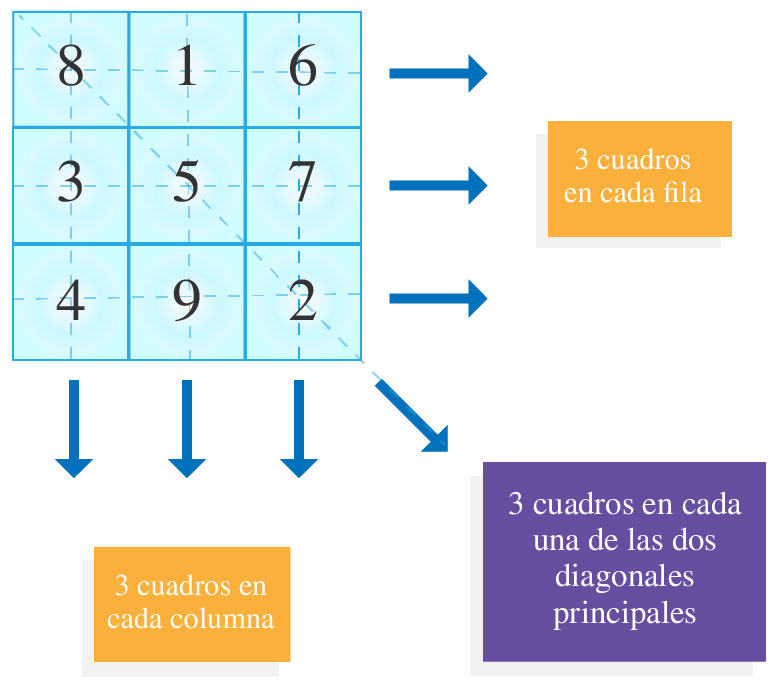
Ahora veamos otro procedimiento para determinar la suma de las diagonales, renglones y columnas del cuadrado mágico de tamaño de $3x3$, tal como se presenta en la tabla:
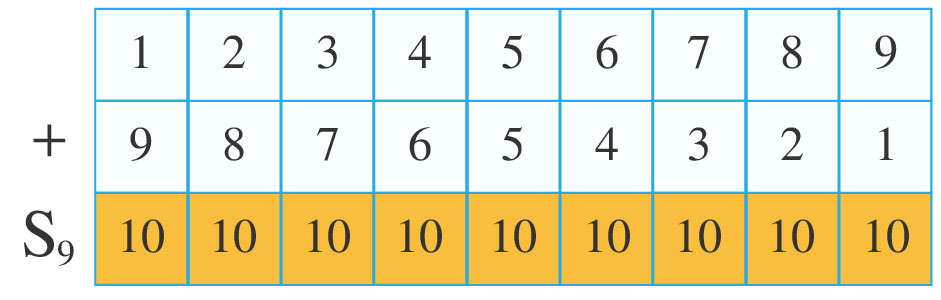
Como podemos observar de la tabla, la primera fila representa a los números naturales desde $1$ hasta $9$ en orden creciente, mientras que el segundo renglón muestra a los mismos números en orden decreciente y el tercero la suma de los números en ambos renglones, es decir, estamos sumando dos veces los números mencionados, lo cual es equivalente al producto de nueve veces el número diez y lo representamos con la expresión ${2S}_9=9\cdot{}10$, de ésta al despejar $S_9$ resulta $S_9=\frac{9\cdot{}10}{2}=45$.
Ahora bien, ¿te parecería práctico sumar los números naturales para un cuadrado mágico de tamaño $100x100$?, por supuesto que no. Como alternativa busquemos un patrón de comportamiento para determinar la suma de los primeros 100 números naturales, es decir, la suma de $1, 2, 3, 4, 5, 6, 7,…, 95, 96, 97, 98, 99$ y $100$. Para ello, consideremos la adición de estos números como aparece en la siguiente tabla:
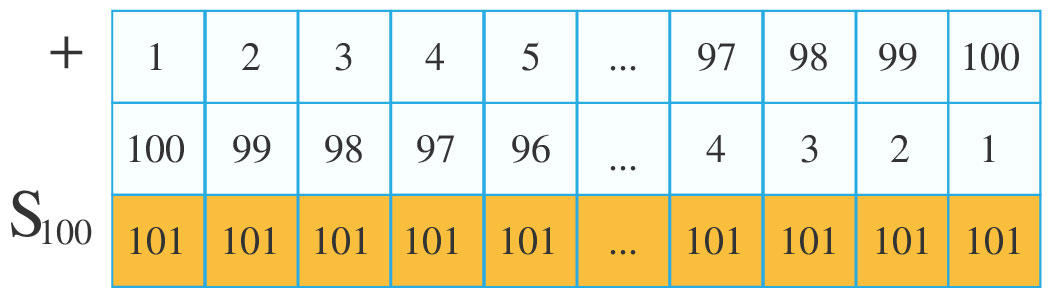
En la tabla se suman dos veces los números naturales del $1$ al $100$ de forma ascendente y de forma descendente, es decir, se suman dos veces los números naturales desde el 1 hasta el $100$, lo cual equivale a multiplicar $100$ veces el número $101$, ya que es el número total de sumandos de la adición y la representamos con la expresión $2S_{100}=100\cdot{}101$, de ésta al despejar $S_{100}$, se obtiene $S_{100}=\frac{100\cdot{}101}{2}=5050$. Si deseamos generalizar la adición para los $n$ primeros números naturales, se realiza el mismo procedimiento para determinar la suma de los primeros $100$ números naturales, considerando $n$ en lugar de $100$, tal como se presenta en la siguiente tabla:
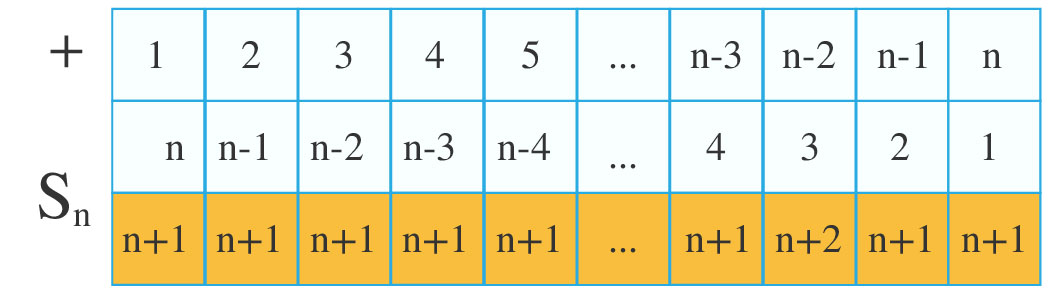
Con base en la fórmula para obtener la suma de los primeros $10$ y $100$ números naturales se concluye que el patrón para determinar la suma de los $n$ primeros números naturales es:
$S_n=\frac{n\left(n+1\right)}{2}$
Ejemplo 1
Determinar la suma para los primeros $9$ números naturales con el patrón obtenido:
$S_9=\frac{9\left(9+1\right)}{2}=\frac{9\left(10\right)}{2}=\frac{90}{2}=45$
Cabe mencionar que el patrón obtenido también se puede utilizar para determinar la suma de números naturales consecutivos, aunque el menor de éstos sea diferente de uno, tal como se ilustra con el siguiente ejemplo.
Ejemplo 2
Determinar la suma de los números naturales $5, 6, 7, 8, 9, 10, 11, 12$ y $13$, mediante el patrón para obtener la suma de los primeros n números naturales, representada con $S_{5,13}$.
Solución. Se aplica el patrón para los primeros trece números naturales y se le restan los cuatro primeros, ya que se sumaron de más, por lo que la suma es:
$S_{13}=\frac{13\left(13+1\right)}{2}=\frac{13\left(14\right)}{2}=\frac{182}{2}=91$
$S_4=\frac{4\left(4+1\right)}{2}=\frac{4\left(5\right)}{2}=\frac{20}{2}=10$
${S_{5,13}=Suma}_{13}-{Suma}_4=91-10=81$


