El término ‘racional’ se deriva de la razón o división de dos números enteros, proviene del latín ratio y del griego razón (λόγος). Conceptual e históricamente, los números racionales aparecen antes que el uso del cero y de los números negativos como una necesidad de dividir algo en partes, generalmente de proporciones iguales.
Los egipcios utilizaron este tipo de números para indicar que una unidad puede dividirse en partes; también conocían el concepto de recíproco de un número entero, definido como el cociente de dividir 1 entre cualquier otro entero ($ \frac 1 1 , \frac 1 2 , \frac 1 3 , \frac 1 4 , \frac 1 5 , … $). El concepto de “fracción egipcia” permite obtener un número racional como la suma de varias fracciones unitarias (con numerador igual a 1), por ejemplo $ 0.95 = \color {Red} {\frac 1 2} \color {Black} + \color {Green} {\frac 1 4} \color {Black}+ \color {Blue} {\frac 1 5} $
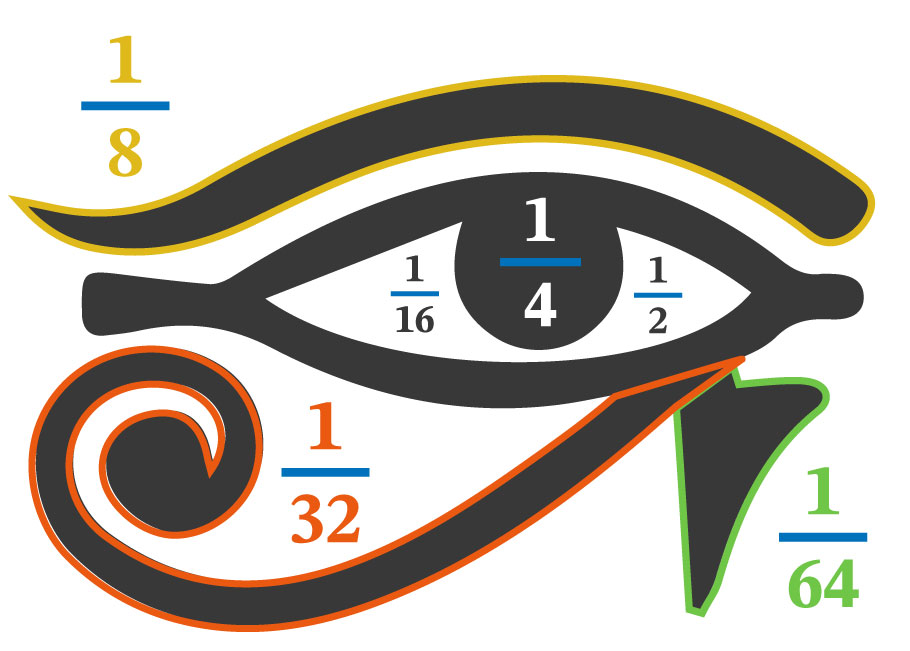
Ojo de Horus egipcio. Cada parte representada por jeroglíficos representa un número racional.
Para los griegos, cualquier cantidad podía expresarse como el cociente de enteros, lo que da origen a los números racionales.
Algunos números con decimales también son representaciones de números racionales; incluyendo las representaciones porcentuales, como puedes observar en los siguientes ejemplos:

Los números racionales surgen como una necesidad de resolver problemas que involucran división de un “todo”, como cuando se habla de la mitad de una parcela, o repartir una pizza entre varios comensales, aplicar un impuesto a algún producto, etc. En las representaciones matemáticas, surge al intentar resolver problemas que involucran ecuaciones que pueden parecer tan simples como obtener el valor de una variable en expresiones como $ 5x-3=1 $ (al despejar $ x= \frac 4 5 $), los cuales no generan soluciones enteras.
Dado que cualquier entero puede dividirse entre 1 $ ( \frac{1}{1} , \frac{2}{1} ,\frac{3}{1} , \frac{4}{1} ... ) $ , los números enteros también son racionales, ya que se trata de un cociente de enteros. Por lo tanto, los números enteros $ \mathbb{Z} $ son un subconjunto de los números racionales $ \mathbb{Q} $.
En general, un número racional se define como cualquier número que puede representarse por una relación o cociente de dos números enteros ($a$ y $b$), donde el denominador debe ser distinto de cero. El término ‘racional’ alude a una razón o fracción o parte de un todo. Además del sistema decimal, cualquier sistema de numeración posicional funciona de la misma forma (binario, hexadecimal, maya, etc).
Los números racionales, además de la notación de cociente, pueden expresarse a través de una cantidad con un número finito de decimales (todos los números con decimales finitos son racionales) o como una sucesión periódica infinita de números.
Adicionalmente, los números racionales forman conjuntos infinitos de fracciones equivalentes, por ejemplo $ \frac 1 2 = \frac 2 4 = \frac 3 6 = \frac 4 8 = ... $ donde puede obtenerse un número que no puede reducirse más (en este caso: $ \frac 1 2 $ ).
No todas las cantidades expresadas con decimales son números racionales; ya que existe otro conjunto que no puede expresarse como un cociente de enteros, y sólo pueden representarse a través de una serie aperiódica (sin repeticiones), como el número $ \pi = 3.141582653... $. Finalmente, el conjunto formado por los racionales e irracionales conforman a los números reales.
Con este material reconocerás las distintas simbolizaciones de los números racionales a través de sus equivalencias para aplicarlas a problemas aritméticos y en contexto.


