El Triángulo de Sierpinsky es un fractal que se construye a partir de cualquier triángulo, que llamaremos triángulo original; sobre éste se traza otro triángulo uniendo sus puntos medios; de los triángulos resultantes, el central se ilumina de color negro; luego, con los puntos medios de los triángulos no iluminados se construyen otros triángulos; de éstos, los centrales se iluminan de color negro; repitiendo el proceso con los puntos medios de los triángulos no iluminados se construye el triángulo de Sierpinsky.
En el video se te explica la construcción del triángulo de Sierpinsky; presta atención a éste para que identifiques algunas de sus regularidades.
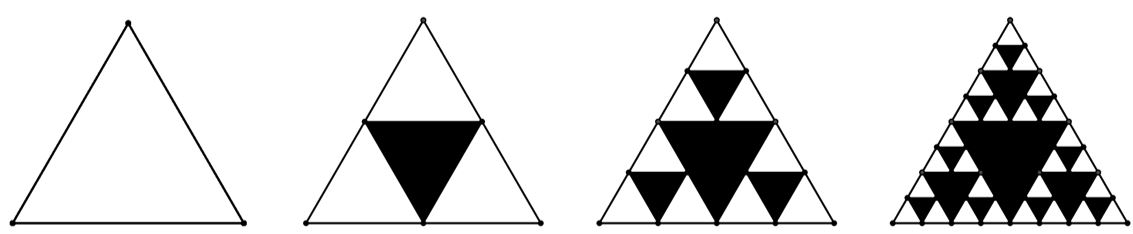
Número de triángulos iluminados
En la construcción del triángulo de Sierpinsky presentada en el video, se observa que en el paso 1 del proceso $n$ se obtiene $1$ nuevo triángulo iluminado; en el paso 2 se obtienen $3$ nuevos triángulos iluminados; y en el paso 3 se obtiene $9$ nuevos triángulos iluminados. Considerando la regularidad que presentan los triángulos iluminados, responde la pregunta, ¿cuántos nuevos triángulos iluminados se obtienen en los pasos 4, 5 y 15 del proceso?, la respuesta escríbelas en los recuadros.
Los triángulos iluminados en la construcción del triángulo de Sierpinsky forman la sucesión 1, 3, 9, 27, 81, 243, 729, 2187, etc. Con base en ésta, escribe en el recuadro la opción con la expresión matemática que genera la sucesión; en estas expresiones $n$ es un número natural y representa el paso $n$ del proceso en la construcción del triángulo de Sierpinsky.
Área del triángulo de Sierpinsky
En el video se te explica los procedimientos algebraicos para obtener el área de cada nuevo triángulo iluminado; presta atención a éste para que identifiques algunas de sus regularidades.
Recuerda que el área de cualquier triángulo se obtiene con la fórmula $A=\frac{ba}{2}$, donde $b$ y $a$ representan la altura y la base del triángulo, respectivamente. En consecuencia, para determinar el área del triángulo de Sierpinsky, primero se obtiene el área del triángulo original; consideramos como triángulo original al triángulo equilátero de longitud de lado 1 m para simplificar los cálculos.
El área del triángulo original se utiliza para obtener el área de los triángulos iluminados en cada paso $n$ del proceso, considerando la proporción de $\frac{1}{4}$ al área del triángulo original en cada paso $n$ del proceso mencionado.
El video te explica los procedimientos algebraicos para obtener la longitud de la altura $b$ del triángulo equilátero $ABC$ de lado 1 m, su área y el área de los triángulos iluminados. Presta atención a los procedimientos utilizados para que descubras la regularidad que presentan el área de los triángulos.
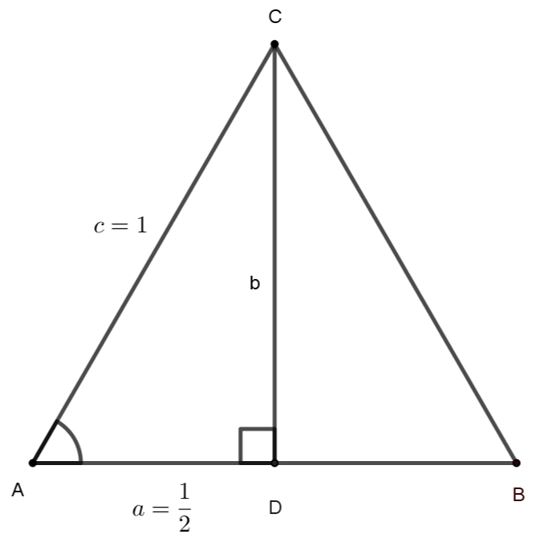
Con base en el video, escribe la opción en el recuadro que corresponde al área del triángulo equilátero de longitud de lado 1 m


