En este apartado representamos gráficamente la longitud $l_{n}$ , el área $C_{n}$ y la suma de las áreas de los cuadrados inscritos $A_{n}$ , mostrados en la tabla. Observarás que las representaciones gráficas te permitirán calcular los valores límite.
Para el registro gráfico de la longitud del lado $l_{n}$ de los cuadrados inscritos se consideran las columnas $1$ y $2$ de la tabla y se grafican en el plano cartesiano, tomado del eje horizontal el paso $n$ del proceso y en el eje vertical las longitudes de los cuadrados $C_{n}$ tal como se muestra en la figura.
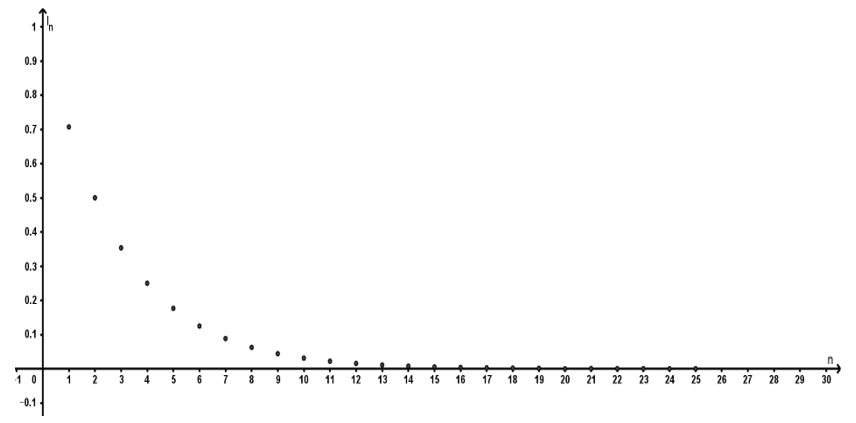
Con base en la tabla de las longitudes de los cuadrados inscritos y su representación gráfica, contesta lo que se te pide:
Para la representación gráfica de las áreas de los cuadrados inscritos $C_{n}$ se consideran las columnas $1$ y $3$ de la tabla y se grafican en el plano cartesiano, tomado del eje horizontal el paso $n$ del proceso y en el eje vertical, el área de los cuadrados $C_{n}$ tal como se muestra en la figura.
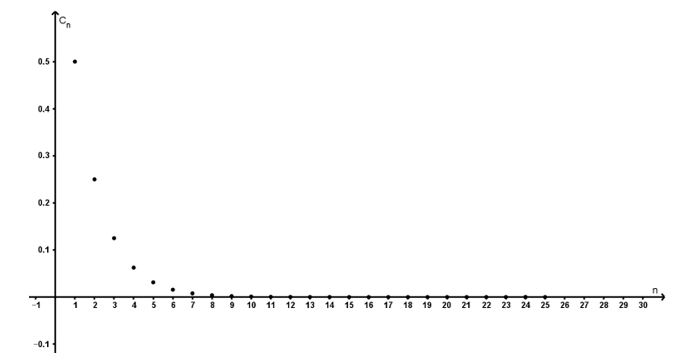
Con base en la tabla de las áreas de los cuadrados inscritos y su representación gráfica, contesta lo que se te pide:
En la representación gráfica de la suma de las áreas de los cuadrados inscritos $A_{n}$ se consideran las columnas $1$ y la suma de las áreas de la columna $3$ de la tabla y se grafican en el plano cartesiano, tomando del eje horizontal el paso n del proceso y en el eje vertical la suma de las áreas de los cuadrados $A_{n}$ tal como se muestra en la figura.
Con base en la tabla de la suma de las áreas de los cuadrados inscritos y su representación gráfica, contesta lo que se te pide:
En concordancia con la resolución del problema es importante que comprendas que, en un proceso infinito, te puedes aproximar tanto como tú quieras al valor deseado.
En la siguiente pantalla explicaremos el Triángulo de Sierpinsky.


