Con la intención de reafirmar los conocimientos presentados acerca de los procesos infinitos, resuelve estos cinco problemas:
Problema del saltamontes
Un saltamontes se encuentra en la orilla de una roca; a un metro de distancia se encuentra un mosquito posado sobre una ramita. El saltamontes avanza en la dirección del mosquito, de manera que, con cada salto que da cubre la mitad de la distancia que le falta para llegar al punto donde está el mosquito.
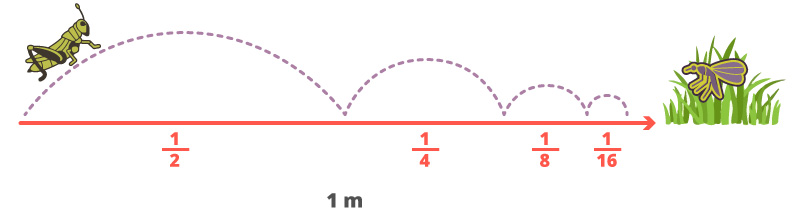
La figura representa los primeros cuatro saltos del saltamontes en dirección del mosquito, ¿cuántos saltos necesitará dar para atrapar al mosquito?, escribe la respuesta en el recuadro.
Para un mejor análisis del paso $n$ del proceso que realiza el saltamontes para atrapar el mosquito; en la tabla se presenta el número de salto, distancia de cada salto y la distancia recorrida.
Analiza la secuencia que se forma con la distancia que recorre el saltamontes en cada salto. Escribe en los recuadros del último renglón las expresiones que generalizan los casos particulares.
Con base en la tabla se observa que la sucesión que incluye la distancia de cada salto que da el saltamontes forma una progresión geométrica, escribe en el recuadro la opción para su razón común y la expresión de la distancia del salto $D_{9}$.
a)
b)
Ahora escribe en los recuadros la opción para obtener el límite de la distancia de los saltos cuando el saltamontes da infinitos saltos y la suma de la distancia que recorre.
a)
b)
Análisis gráfico de la distancia que recorre el saltamontes
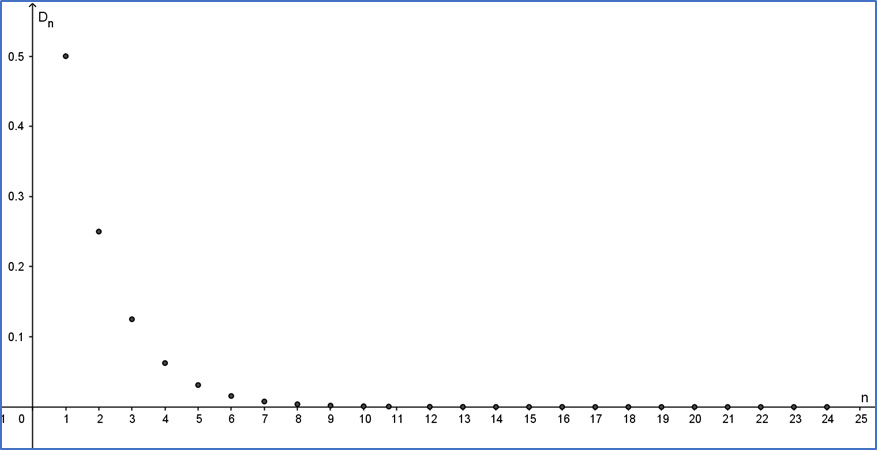
La gráfica de la distancia que recorre el saltamontes en cada salto que da, se presenta en la
figura. Con base en ésta y
considerando que el número de pasos tiende a infinito, contesta la pregunta, ¿cuál es la distancia que recorre el saltamontes?, la
respuesta escríbela en el recuadro.
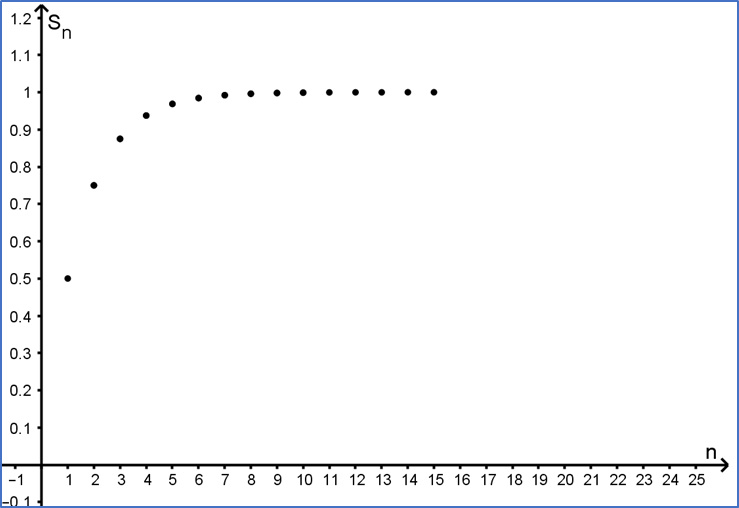
La gráfica de la suma de las distancias que recorre el Saltamontes en los saltos que da, se presenta en la figura. Con base en ésta y considerando que el número de pasos tiende a infinito, contesta la pregunta, ¿cuál es la suma de las distancias que recorre el saltamontes?, la respuesta escríbela en el recuadro.
Curva de Koch
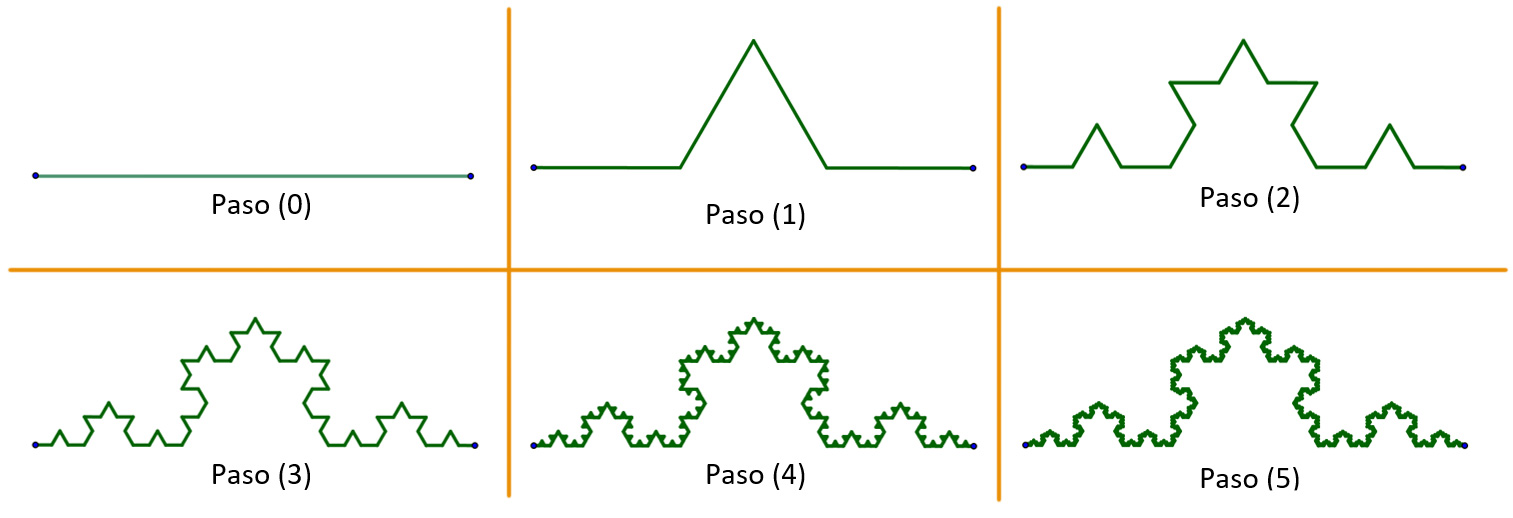
La curva de Koch es otro de los fractales que se construye sobre un segmento de recta, tal como se indica.
- a) Dividir el segmento en tres partes iguales.
- b) Sobre el segmento central construir un triángulo equilátero.
- c) Borrar el segmento central, es decir, la base del triángulo.
- d) Repite el proceso sobre cada nuevo segmento.
La construcción de la cueva de Koch se ilustra en el video «Construcción de la curva de Koch»; presta atención para que descubras regularidades que se presentan. En la figura se te muestran los primeros cinco pasos de su construcción.
Determina la longitud de la curva de Koch considerando la longitud del segmento 1 metro para facilitar los procesos algebraicos; para ello, observa el video «Longitud de la curva de Koch». Escribe la respuesta a las preguntas y para los incisos restantes escribe en el recuadro la opción que corresponde:
B)
C)
E)
Rebote de una pelota
Se deja caer una pelota desde una altura de 10 metros. Cada rebote alcanza $\frac{1}{2}$ de la altura del rebote anterior hasta que queda en reposo, ¿Cuál es la distancia total que recorre la pelota (hacia arriba y hacia abajo) desde que se deja caer hasta que queda en reposo?

En la resolución del problema considera la figura que representa las distancias que recorre la pelota hacia abajo y hacia arriba; con base en esto, relaciona las columnas Conceptos y Expresiones; escribe la opción según corresponda en la tabla.
| Expresión de la distancia hacia abajo | $A$ | $10+20\left ( \frac{1}{2}+\left ( \frac{1}{2} \right )^{2}+\left ( \frac{1}{2} \right )^{3} +\left ( \frac{1}{2} \right )^{4}+\cdots +\left ( \frac{1}{2} \right )^{n}\right )$ |
|---|---|---|
| Expresión de la distancia hacia arriba | $B$ | $30$ m |
| Expresión de la distancia total | $C$ | $\frac{1}{2}\left ( 10 \right )+\left ( \frac{1}{2} \right )^{2}\left ( 10 \right )+\left ( \frac{1}{2} \right )^{3}\left ( 10 \right )+\left ( \frac{1}{2} \right )^{4}\left ( 10 \right )+\cdots +\left ( \frac{1}{2} \right )^{n}\left ( 10 \right )$ |
| Razón de la progresión geométrica | $D$ | $10+\frac{1}{2}\left ( 10 \right )+\left ( \frac{1}{2} \right )^{2}\left ( 10 \right )+\left ( \frac{1}{2} \right )^{3}\left ( 10 \right )+\cdots +\left ( \frac{1}{2} \right )^{n}\left ( 10 \right )$ |
| Distancia total | $E$ | $\frac{1}{2}$ |
Construir un laberinto espiral
Construye un laberinto espiral en un terreno que mide 1000 m por 1000 metros. Comienzas por construir las bardas exteriores y luego las interiores. La distancia entre las bardas que forman el laberinto debe ser siempre de un metro.
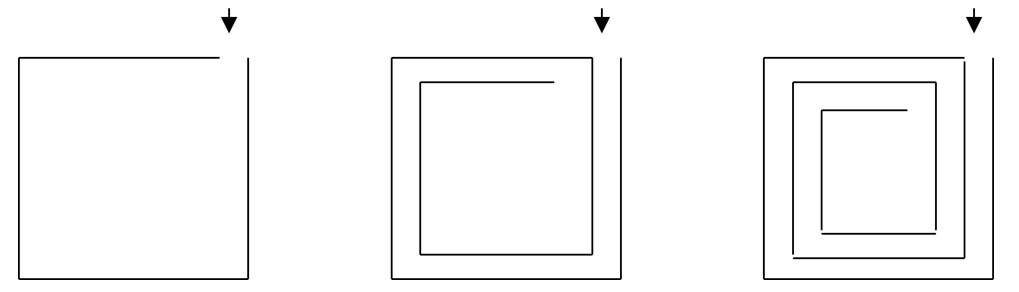
Dibuja en tu cuaderno un esquema del laberinto con todas las bardas que puedas dibujar (Ignora el ancho de la barda). Observa la figura que obtienes, y responde las preguntas.
Volumen de un cono

El volumen de un cono se calcula con el método exhaustivo de Eudoxio. Éste consiste en un procedimiento geométrico de aproximación a un resultado, con el cual el grado de precisión aumenta en la medida en que avanza el cálculo.
El video Volumen de un cono te explica el procedimiento exhaustivo para obtener el volumen del cono. Como aplicación de éste, se te presenta una tabla para que establezcas el volumen del cono y escríbelo en el recuadro.
| Número de lados del polígono $n$ | Volumen pirámide $V_{n}$ | Volumen pirámide $V_{n}$ con decimal |
|---|---|---|
| 3 | $\frac{1}{3}\left ( 3 \right )Sen\left ( \frac{\pi }{3} \right )Cos\left ( \frac{\pi }{3} \right )r^{2}h$ | $\frac{1}{3}\left ( 1.29904 \right )r^{2}h$ |
| 10 | $\frac{1}{3}\left ( 10 \right )Sen\left ( \frac{\pi }{10} \right )Cos\left ( \frac{\pi }{10} \right )r^{2}h$ | $\frac{1}{3}\left ( 2.93893 \right )r^{2}h$ |
| 50 | $\frac{1}{3}\left ( 50 \right )Sen\left ( \frac{\pi }{50} \right )Cos\left ( \frac{\pi }{50} \right )r^{2}h$ | $\frac{1}{3}\left ( 3.13333 \right )r^{2}h$ |
| 100 | $\frac{1}{3}\left ( 100 \right )Sen\left ( \frac{\pi }{100} \right )Cos\left ( \frac{\pi }{100} \right )r^{2}h$ | $\frac{1}{3}\left ( 3.13953 \right )r^{2}h$ |
| 200 | $\frac{1}{3}\left ( 200 \right )Sen\left ( \frac{\pi }{200} \right )Cos\left ( \frac{\pi }{200} \right )r^{2}h$ | $\frac{1}{3}\left ( 3.14108 \right )r^{2}h$ |
| 500 | $\frac{1}{3}\left ( 500 \right )Sen\left ( \frac{\pi }{500} \right )Cos\left ( \frac{\pi }{500} \right )r^{2}h$ | $\frac{1}{3}\left ( 3.14151 \right )r^{2}h$ |
| $n$ | $\frac{1}{3}\left ( n \right )Sen\left ( \frac{\pi }{n} \right )Cos\left ( \frac{\pi }{n} \right )r^{2}h$ | $\frac{1}{3}\left ( n \right )Sen\left ( \frac{\pi }{n} \right )Cos\left ( \frac{\pi }{n} \right )r^{2}h$ |
| $\frac{1}{3}\pi r^{2}h$ | $\frac{1}{3}\pi r^{2}h$ |
Con base en el video, el recurso GeoGebra y la tabla, escribe la opción en el recuadro que corresponde al valor del límite de las pirámides regulares cuando el número de lados de los polígonos tiende a infinito.
A)
B)
C)
Fin de actividad final


