Papiro de Rhind
A. Henry Rhind, un escocés estudioso de Egipto, compró un papiro en la ciudad de Luxor en 1858, el cual fue encontrado en las ruinas de Tebas y se le conoce ahora como papiro Rhind o de Ahmes, ya que fue escrito por Ahmes en el siglo 17 a. C. , a partir de escritos que tenían una de antigüedad de 200 años, por lo que no se tiene certidumbre del contenido original. El Museo Británico de Londres resguarda el papiro de Rhind, el cual contiene 87 problemas, que incluyen tanto cuestiones aritméticas y de ecuaciones lineales, como de aspectos geométricos en el cálculo de áreas y volúmenes, donde se ilustran el carácter empírico y específico de las matemáticas egipcias, con resultados prácticos. El papiro empieza con la sugestiva frase "Cálculo exacto para entrar en conocimiento de todas las cosas existentes y de todos los oscuros secretos y misterios", tiene una longitud de 6m por 30 cm de ancho aproximadamente.
El papiro contiene, entre otros, problemas sobre el uso de fracciones, de ecuaciones simples, de cálculo de áreas de triángulos, cuadriláteros y círculos, así como el cálculo del volumen de cilindros y prismas.
A continuación se presentan los problemas 51 y 48 del papiro de Rhind en los que podrás observar el uso empírico de la Geometría Egipcia.
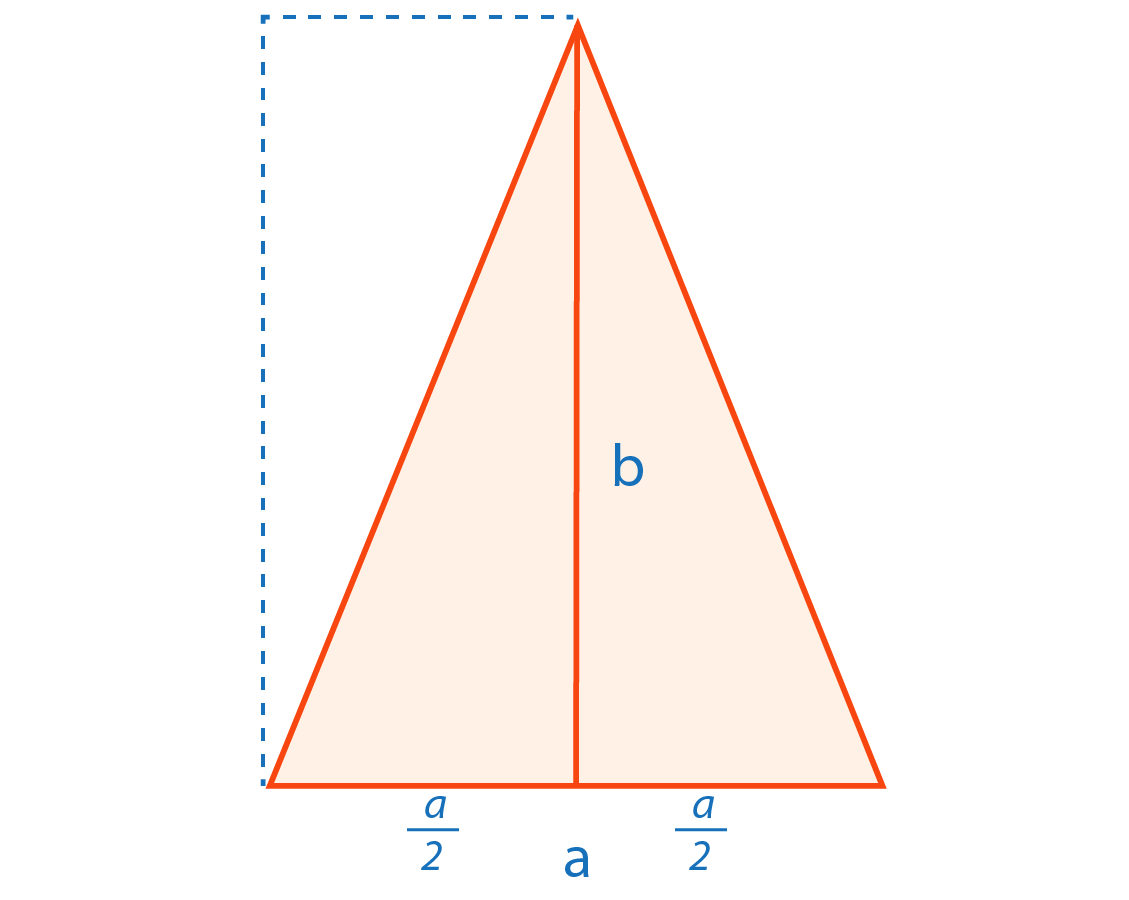
Se muestra que el área de un triángulo isósceles de base $4 jet$ y altura $10 jet$, se encuentra tomando la mitad de la base y multiplicando por su altura. Ahmes sugiere que el triángulo isósceles se puede ver como dos triángulos rectángulos, de tal forma que moviendo uno de ellos de posición, se forme un rectángulo de base $\tfrac{a}{2}$ y altura b. La solución dada concuerda con la la fórmula actual para calcular el área de un triángulo en general:
$A=\tfrac{ab}{2}=\tfrac{(4\;jet)(10\;jet)}{2}=20\;jet^2\;h\;v$
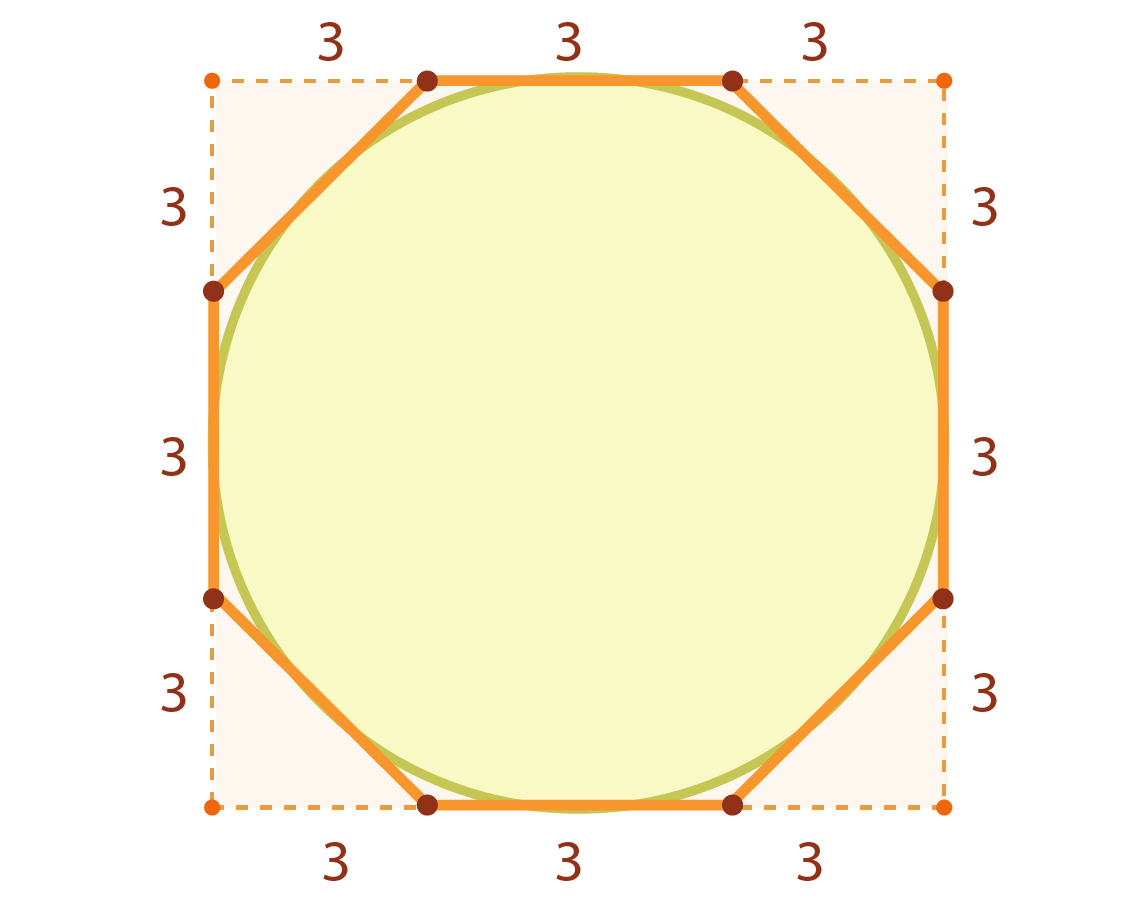
Se aproxima el área de un círculo comparándolo con el área de un cuadrado circunscrito: toma un circulo de diámetro $9$ y lo aproxima con el área de un cuadrado de lado $8$, cuya área es $64 setat$. Se dice que Ahmes hace lo siguiente: los lados del cuadrado circunscrito de lado $9$ los divide en tres partes iguales y quita los cuatro triángulos de las esquinas de área $\tfrac{(3)(3)}{2} =4.5$ cada uno, como se muestra en la figura, por lo que de que queda un octágono de área $(9)(9)-4(4.5)=63$, pero considerando quizás que el área del círculo es un poco mayor a la del octágono, lo aproxima como $64$ setat que es el área del cuadrado de lado $8$.

El área del círculo de radio 4.5 calculada con la fórmula actual es:
$A=\pi r^2 = (3.1415926...)(4.5)^2=63.617251...setat,$
por lo que se puede considerar que $63 setat$ calculada hace más de $3000$ años es una buena aproximación.
Papiro de Moscú
El Papiro de Moscú fue adquirido por el egiptólogo ruso Vladímir Goleníshchev (1856-1947) en el año 1883 y se le conoció como Papiro Goleníshchev. Desde que el Museo Pushkin de Moscú lo compró en 1912 se le conoce como Papiro de Moscú.
El papiro de Moscú escrito hace más de 4000 años mide 8 cm de ancho por 5 m. de largo, contiene 25 problemas de temas cotidianos que muestran el carácter empírico de la Geometría egipcia cuya finalidad era resolver problemas específicos, sin pretender hacer teoría ni establecer reglas generales.
El problema 14 del papiro, mostrado en la figura, es el cálculo del volumen de una pirámide truncada, el cual es uno de los más importantes de las matemáticas egipcias. Se expone a continuación.
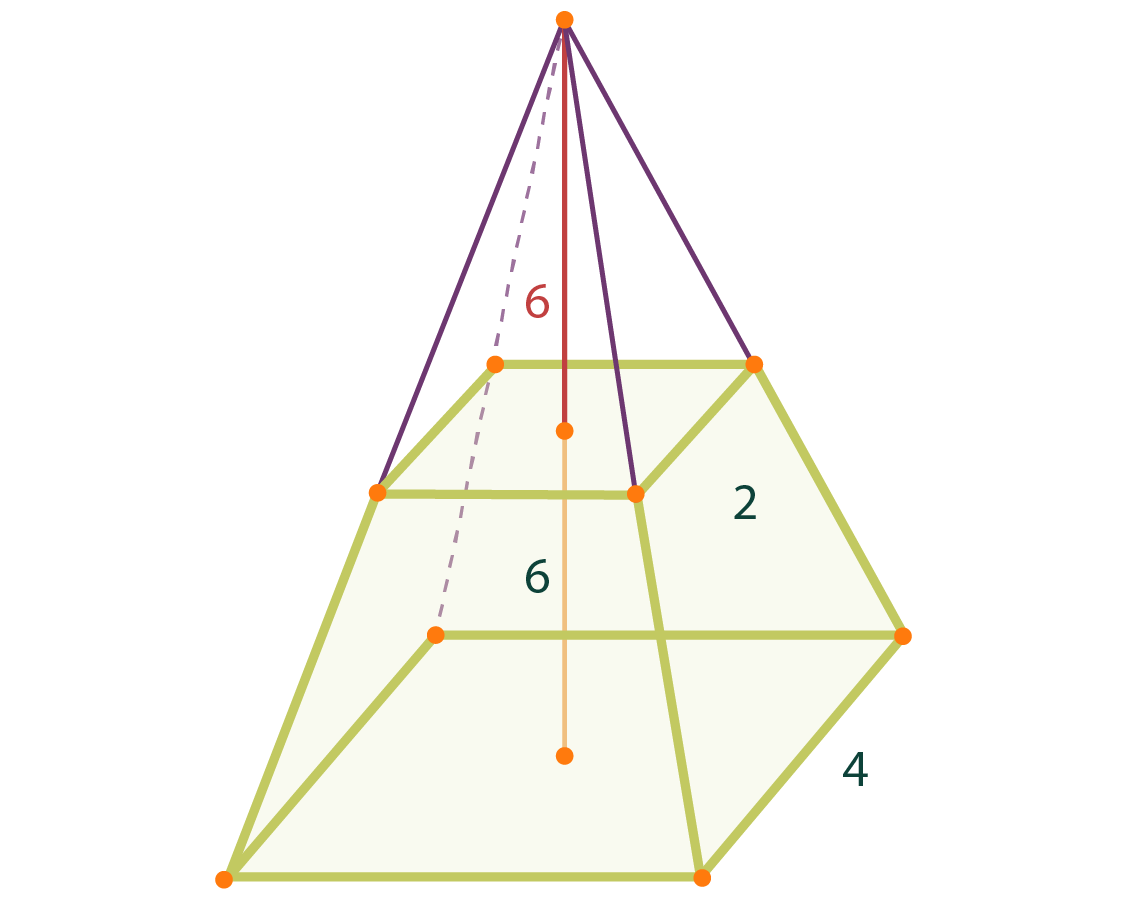
La base de una pirámide truncada es un cuadrado que mide 4 codos por lado, la tapa es un cuadrado cuyos lados miden 2 codos y la altura 6 codos. Se requiere calcular el volumen de la pirámide.

El cálculo se hace de la siguiente manera:
Se encuentra el área de la base $4×4 = 16$ y el área de la tapa $2×2 = 4$, se multiplica el lado de la base por el lado de la tapa $4×2 = 8$ y se obtiene la suman estos números $16+4+8 = 28$. Ahora se toma un tercio de la altura $6÷3=2$ y se multiplica por $28$, dando como resultado $2x28=56$ que es el volumen de la pirámide truncada (el codo era una unidad de medida de los antiguos egipcios, equivalente a $52.3cm$).
El resultado correcto del volumen de la pirámide truncada que obtuvieron los egipcios (mostrada de color rojo en la figura de abajo) se puede comprobar con la fórmula que usamos hoy a partir del volumen de una pirámide completa, $V=\tfrac{1}{3}AH$ donde $A$ es el área de la base de la pirámide y $H$ su altura. El volumen de la pirámide truncada $V_T$ es igual al volumen de la pirámide grande $V_1$ menos el volumen de la pirámide chica $V_2$:
$V_T=V_1-V_2$
El volumen de la pirámide grande, con área de la base $A_1=(4)(4)=16$ y altura $H_1=12$, es $V_1=\tfrac{1}{3}(16)(12)=64 $
El volumen de la pirámide chica, con área de la base $A_2=(2)(2)=4$ y altura $ H_2=6$, es $V_2=\tfrac{1}{3}(4)(6)=8 $
Por tanto, el volumen de la pirámide truncada es $V_T=64-8=56$. Este es el resultado encontrado por los egipcios.
Los papiros de Rhind y de Moscú son los registros más importantes de las matemáticas egipcias.


