Entre Thales en 600 a.C y Euclides en 300 a. C. se desarrolló la noción de un discurso lógico como una sucesión de principios obtenidos por razonamiento deductivo a partir de un conjunto principios iniciales y definiciones. Cuando se presenta un argumento por procedimientos deductivos, cualquier argumento tendrá que deducirse de principios previos. Como este esquema no puede continuar hacia atrás indefinidamente, se requiere una colección de principios primarios cuyas verdades sean aceptables, para deducir todos los otros principios del discurso.
La contribución más sobresaliente de los antiguos griegos a las matemáticas fue la argumentación deductiva como método de conocimiento. Los Elementos de Euclides es el mejor ejemplo del desarrollo extenso de esta argumentación. En el discurso lógico los principios primarios se llaman axiomas o postulados y todos los otros principios de discurso que se deducen lógicamente de éstos se les llama teoremas del discurso.

Geometría deductiva
Geometría basada una cadena de razonamientos lógicos sustentados por definiciones, postulados, axiomas y teoremas ya demostrados.
Teorema
Es una proposición de un objeto geométrico que debe ser demostrado.
Postulados
Son proposiciones de objetos geométricos que se admiten sin demostración y son propios de la geometría.
Geometría Griega
Los griegos desarrollaron la geometría de manera importante con la introducción de método deductivo y le dieron un carácter científico a esta disciplina. Entre los matemáticos y filósofos griegos que contribuyeron de manera más importante al desarrollo de la geometría deductiva mencionamos a Thales de Mileto, Pitágoras, Euclides y Arquímedes, con algunos rasgos bibliográficos notables. Da clic en el siguiente fichero para conocer más de ellos:
-
Thales de Mileto
Nació por el año 640 a. C en la ciudad de Mileto, antigua ciudad situada en la costa occidental de Jonia, que actualmente es Turquía. De joven se dedicó al comercio y asuntos públicos destacando en estas actividades. En esta etapa de su vida visitó Egipto, donde estudió Astronomía y Geometría, calculó la altura de la Gran Pirámide de Egipto midiendo al mismo tiempo la sombra que produce la pirámide y un bastón o la de él, formando triángulos semejantes y aplicando el llamado teorema de Thales (Sanchéz, 2011).
Posteriormente fundó la Escuela de Mileto, primera escuela de matemáticas y filosofía griega, en la cual estuvieron también sus discípulos sobresalientes Anaximandro, Anaxímenes y Pitágoras. Se considera el precursor del pensamiento deductivo aplicado a la geometría y se le atribuyen varios teoremas geométricos importantes, entre ellos, “El ángulo inscrito en un semicírculo es un ángulo recto” y “La suma de los ángulos interiores de un triángulo es igual a dos ángulos rectos”. Fue uno de los más grandes filósofos y geómetras griegos y se le considera uno de los Siete Sabios de Grecia. Thales de Mileto murió en el año 547 a.C a la edad de 90 años.
 Busto de Thales de Mileto (una ilustración de la obra de Ernst Wallis, 1877)
Busto de Thales de Mileto (una ilustración de la obra de Ernst Wallis, 1877) Gradas y restos del edificio de la escena del teatro de Mileto
Gradas y restos del edificio de la escena del teatro de MiletoConoce las contribuciones de Thales de Mileto a la geometría.
-
Pitágoras de Samos
Nació en Samos en 560 a.C., una isla cercana a Mileto (Turquía) y murió en Metaponto alrededor de 500 a.C., es uno de los matemáticos griegos más conocidos en la actualidad por el llamado “Teorema de Pitágoras” que se le atribuye a él, en el cual establece la relación entre los lados de un triángulo rectángulo. Contribuyó al desarrollo de la matemática griega, más allá del conocimiento empírico de los babilonios y egipcios, con una tendencia formal. Fue fundador de la Escuela Pitagórica, que además del su carácter religioso estudiaba aspectos cosmológicos, filosóficos y éticos, entre otros. Al parecer, las palabras “filosofía” (amor a la sabiduría) y “matemáticas” (aquello que se aprende) fueron términos acuñados por Pitágoras para describir actividades intelectuales. Aunque no se cuenta con escritos originales de Pitágoras, sus discípulos le atribuyen a él avances importantes en diferentes áreas de conocimiento, como en el desarrollo de la filosofía racional y de la teoría musical (Sanchéz, 2011).

Entre los descubrimientos matemáticos que se atribuyen a la escuela Pitagórica se encuentran los siguientes:
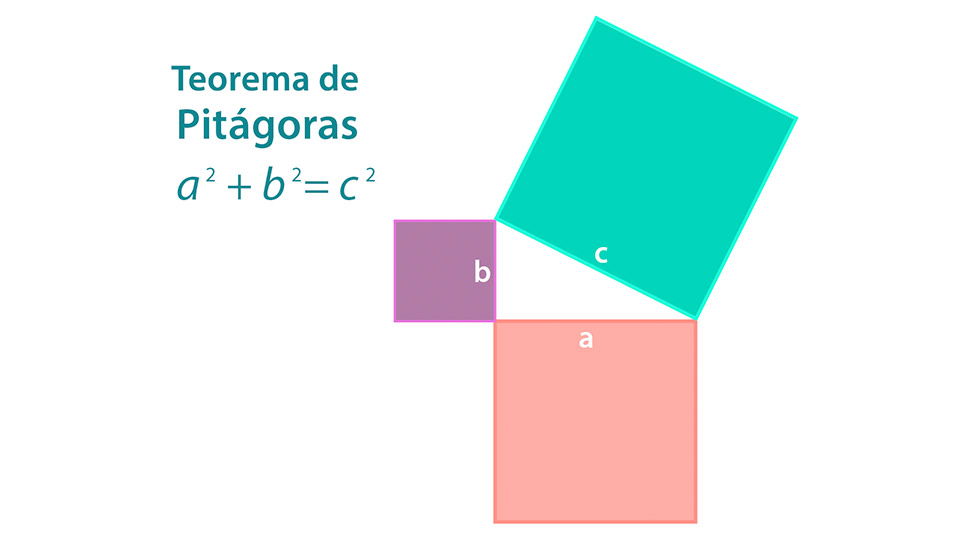
Teorema de Pitágoras
Este teorema establece que en un triángulo rectángulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. (Ve la figura). Aunque se sabe que esta relación era conocida y utilizada por los babilonios y egipcios en casos particulares, fueron los pitagóricos quienes dieron una demostración formal y la cual aparece en la obra de los “Elementos de Euclides”.
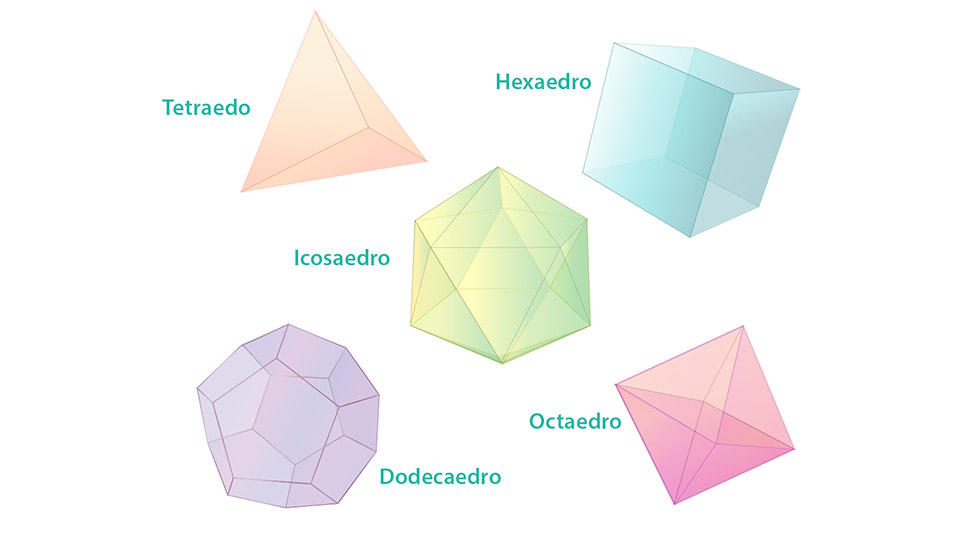
Los Sólidos perfectos
Se considera que los pitagóricos hicieron la demostración de que solamente se pueden tener 5 poliedros regulares: tetraedro (4 caras), cubo (6 caras), octaedro (8 caras), dodecaedro (12 caras) e icosaedro (20 caras), como se muestran en la figura.
La irracionalidad de la raíz cuadrada de 2
El descubrimiento de que la diagonal de un cuadrado de lado 1 no puede expresarse como un cociente de números enteros, lo que da origen a los llamados números irracionales.
Los Ángulos interiores de un triángulo
La suma de los ángulos interiores de un triángulo es igual a rectos.
-
Euclides
Euclides (330-275 a.C.) es uno de los grandes matemáticos griegos. Por la gran influencia que tuvo su obra a lo largo de la historia, especialmente los Elementos, se le considera uno de los más ilustres de todos los tiempos.
Euclides sistematizó mucho del conocimiento geométrico que le antecedió, desarrollando una teoría axiomática rigurosa, que en mucho sigue vigente en nuestra época y sirve como modelo de enseñanza de la formación matemática, ya que partir de una serie de definiciones, postulados y axiomas, estableció por rigurosa deducción lógica un conjunto de teoremas, plasmados en su obra maestra los Elementos, considerada uno de los logros más importantes del intelecto humano y da lugar a lo que se conoce como geometría euclidiana.
Euclides abrió en Alejandría la escuela más importante de Grecia, alcanzando un gran prestigio como maestro. Como muchas veces sucede, se dice que el rey le pidió que le mostrara un procedimiento abreviado para acceder al conocimiento de las matemáticas, a lo que Euclides le dijo que no existía una vía así para llegar a la geometría. Se dice también que un joven principiante en el estudio de la geometría le preguntó qué ganaría con su aprendizaje, a lo que Euclides contestó explicándole que la adquisición de un conocimiento es siempre valiosa en sí misma, pero además le dio algunas monedas.

Los Elementos de Euclides
Constan de 13 libros, en cada uno de ellos trata los siguientes temas, a través de la deducción lógica rigurosa: del libro 1 al 6 propiedades de la geometría plana, del libro 7 al 10 propiedades de la teoría de números y del libro 11 al 13 propiedades de la geometría de sólidos.
El libro I de los Elementos de Euclides, del cual expondremos dos teoremas como ejemplo para ilustrar el trabajo de Euclides, empieza con 23 definiciones, cinco postulados y cinco nociones comunes, y con ellos va demostrando detallada y rigurosamente 48 proposiciones o teoremas, utilizando algunos de éstos que ya demostró como argumento o la razón en otras proposiciones. La demostración de un teorema de Euclides es un razonamiento compuesto por una cadena de afirmaciones fundamentadas en razones que pueden ser definiciones, postulados, nociones comunes, otros teoremas ya demostrados o la hipótesis del teorema, hasta llegar finalmente a la tesis del teorema que se quiere demostrar. Esta es la metodología de la geometría deductiva que desarrolló Euclides en cada uno de sus trece libros.
Revisa cuidadosamente los ejemplos del Ejercicio 3, lo importante es que cada afirmación que se hace en la demostración tiene una razón que la fundamenta.
Otras obras de Euclides
Sólo se tienen referencias o breves resúmenes de comentaristas posteriores: En los tratados Lugares superficiales y las Cónicas se tienen al parecer resultados expuestos posteriormente por Apolonio de Perga. En la obra los Porismas se desarrollan los teoremas geométricos denominados actualmente de tipo proyectivo; de esta obra sólo se conservan el resumen trazado por Pappo de Alejandría. En Óptica y Catóptrica se estudiaban las leyes de la perspectiva, la propagación de la luz y los fenómenos de reflexión y refracción.
-
Arquímedes de Siracusa
Nació en 287 a.C. en Siracusa, Sicilia, de la Gran Grecia (hoy Italia) y murió en el sitio de Siracusa implementado por los romanos 212/211 a. C., donde tuvo un papel muy importante en su defensa construyendo máquinas de guerra tan efectivas que retrasaron la toma de Siracusa. Además de matemático, sobresalió como físico, ingeniero y astrónomo (Tommer, 2019).
Entre sus muchas y diversas aportaciones a las ciencias y la técnica destacan fundamentos de la hidrostática y estática, el principio de Arquímedes de cuerpos sumergido en líquido, el principio de la palanca, el tornillo de Arquímedes para elevar el agua, un cálculo muy preciso del número π, el método de exhaución para calcular áreas y volúmenes, la relación entre el área y el volumen de una esfera y del cilindro circunscrito, etc. Tuvo gran influencia en grandes matemáticos de los siglos XVI y XVII como Galileo Galilei y René Descartes. Por todas sus contribuciones al conocimiento, se le considera uno de los científicos más importantes de la antigüedad clásica.

 Pintura mural de Giulio Parigi 1599
Pintura mural de Giulio Parigi 1599
Mapa de la Grecia Antigua
Observamos las tres áreas en las que se dividía la Hélade, nombre dado por los antiguos griegos a su territorio, dividido en múltiples estados, las polis:
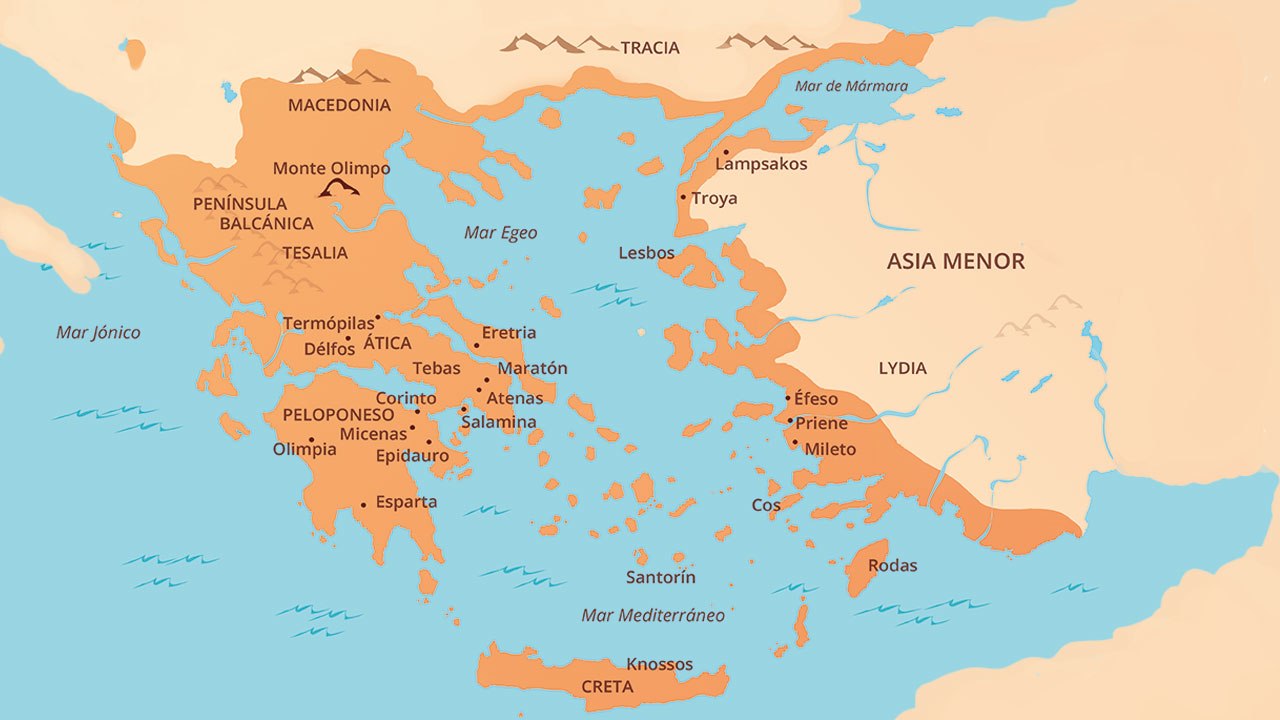
- El área continental europea, el sur de la Península Balcánica, rodeada por el Mar Jónico al oeste y el Mar Egeo al Este. Las regiones en que se divide son Tracia, Macedonia, Tesalia, Ática y el Peloponeso. En este territorio destacan las ciudades de Delfos, Tebas, Eretria, Atenas, Epidauro, Micenas, Corinto, Olimpia y Esparta. Aparecen Maratón y las Termópilas.
- Las islas del Mar Egeo como Creta, Rodas, Santorín, Cos, Salamina y Lesbos.
- Las costas de Asia Menor, donde destaca la región de Lydia, y las ciudades de Lampsakos, Éfeso, Priene y Mileto.
Problemas Clásicos no resueltos
Fieles a la cultura geométrica de los griegos para elaborar y justificar construcciones utilizando únicamente la regla y el compás, como la construcción de un triángulo equilátero ya explicada, hubo tres problemas que se volvieron famosos en la historia de la geometría griega, porque muchos matemáticos los intentaron resolver ignorando que esos problemas no tenían solución utilizando solo esos dos instrumentos, como se demostró hasta el siglo XIX. Los problemas son los siguientes.
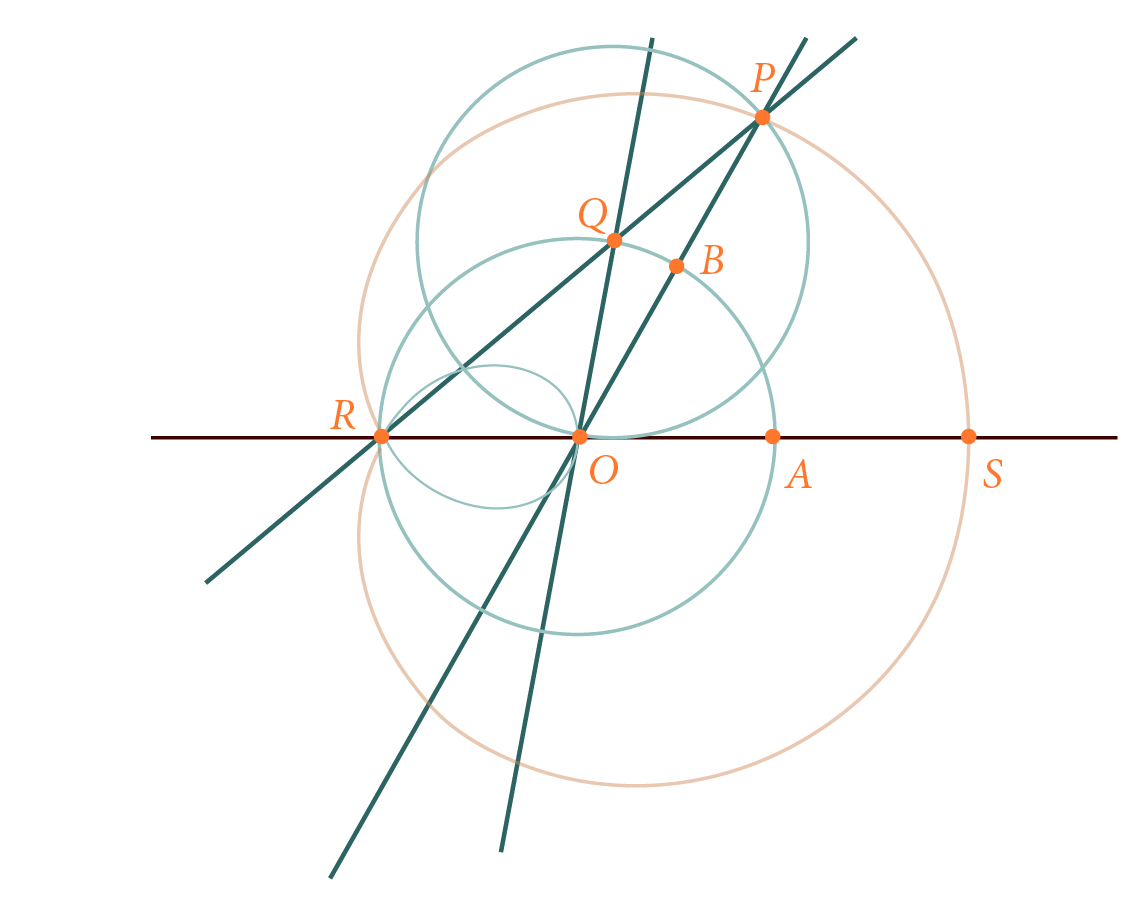
La trisección del ángulo
Es uno de los problemas clásicos de las matemáticas de la antigua Grecia. El problema consiste en encontrar un ángulo cuya medida sea un tercio de otro ángulo dado, utilizando únicamente regla y compás. Sobrevivió sin ser resuelto hasta el siglo XIX por Wantzel quien demostró la imposibilidad de la construcción solo con regla y compás.
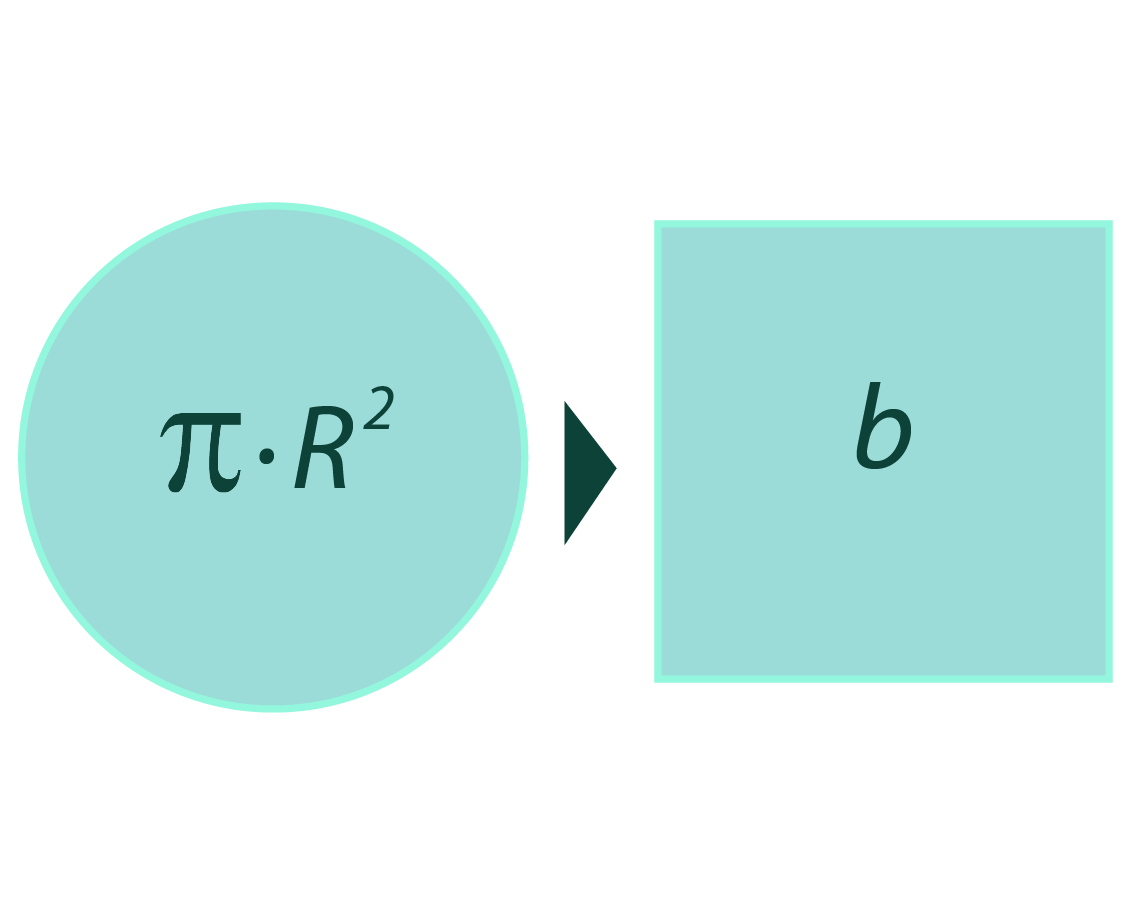
La cuadratura del círculo
No existe un método geométrico que permita construir un círculo y un cuadrado de igual área, utilizando solo regla y compás. Carl Louis Ferdinand von Lindemann en 1882 comprobó esta afirmación.

La duplicación del cubo
Cuenta la leyenda que en el año 429 a. C., muere Pericles, gobernador de Atenas, víctima de la epidemia que sufría la ciudad. Por este motivo algunos de los habitantes fueron a la ciudad de Delfos para hacer consultas al Oráculo de Apolo y saber cómo poder detener la epidemia. La respuesta a la consulta del Oráculo es que deben elaborar un nuevo altar en forma de cubo cuyo volumen duplique el del altar que ya existe. Trataron de resolver el problema, pero también no lograron evitar el desastre por este medio. La pandemia se disipó con el tiempo, pero el problema matemático permaneció.


