Ejercicio - Elementos de Euclides

A continuación se hace la demostración de la proposición I.1 del libro de los Elementos de Euclides, siguiendo la metodología deductiva.

Lee con atención y después escribe los valores que corresponden en la columna de “Razones” de la tabla para la demostración de ambos casos. Posteriormente da clic en Verificar para revisar tus respuestas.

Teorema: Sobre una recta dada y finita construir un triángulo equilátero

Hipótesis. Sea una recta dada (la recta ${\color{Red}{AB}}$)

Tesis. Construir un triángulo equilátero (triángulo ${\color{Red}{ABC}}$)

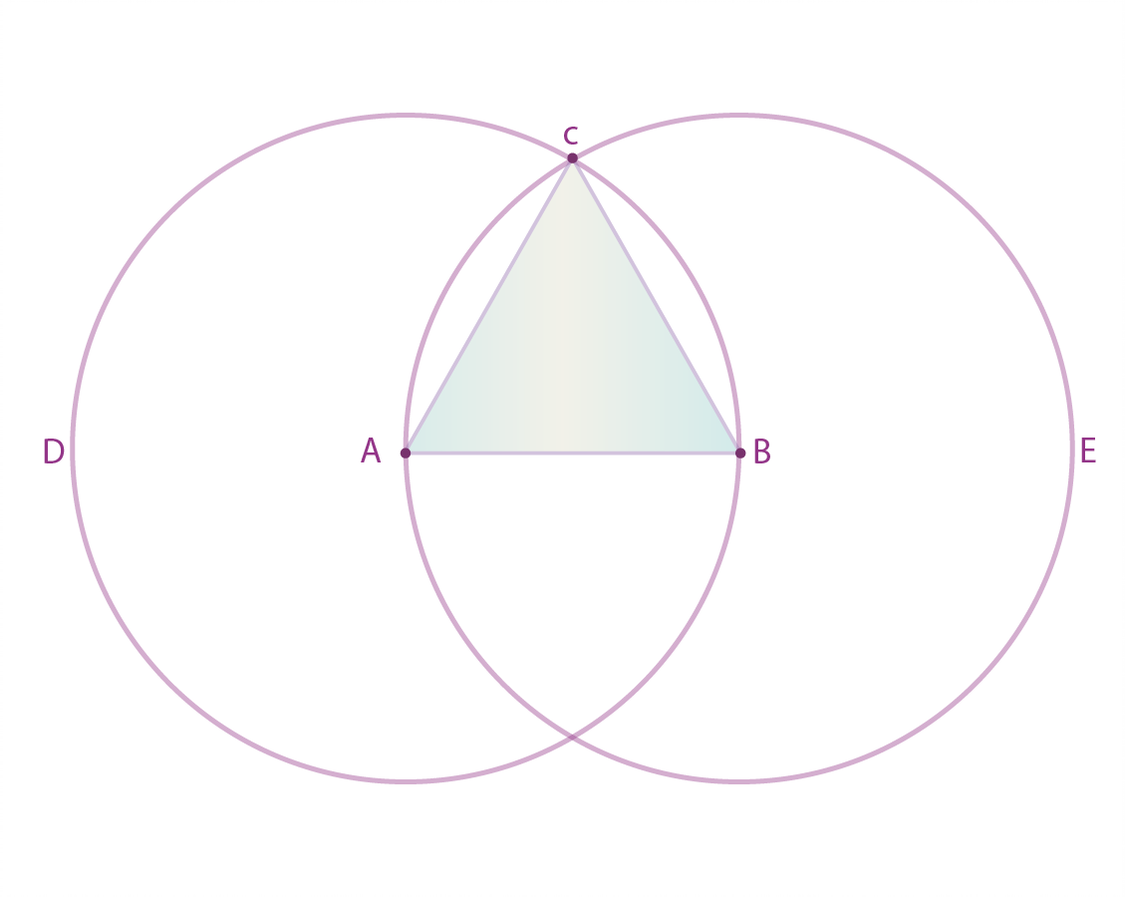
Proposición I.1 Teorema

Con base en la figura se describe cada paso de la demostración.

Razones utilizadas en la demostración de la Proposición I.1 :

Postulado P.1. Trazar una línea recta desde cualquier punto a cualquier otro punto.

Postulado P.3. Describir un círculo desde un punto cualquiera y con una distancia cualquiera.

Definición D.15. Un círculo es una figura plana, limitada por una sola línea tal que todas las rectas que caen sobre ella desde uno de los puntos interiores de la figura son iguales entre sí.

Noción común N.1. Las cosas que son iguales a una misma cosa son iguales entre sí.

Demostración

Afirmaciones Razones
1. ${\color{Red}{AB}}$ es la recta dada y finita Hipótesis
2. Con centro en A y distancia ${\color{Red}{AB}}$ se describe el círculo BCD Afirmación 1 y Postulado P.3
3. Con centro en B y distancia ${\color{Red}{AB}}$ se describe el círculo ACE Afirmación 1 y Postulado
4. Desde el punto C de intersección de los dos círculos se trazan las rectas ${\color{Red}{CA}}$ y ${\color{Red}{CB}}$ Afirmación 2 y 3 Postulado
5. ${\color{Red}{CA}}$ es igual a ${\color{Red}{AB}}$ ya que A es el centro del círculo BCD Afirmación 4 y Definición
6. ${\color{Red}{CB}}$ es igual a ${\color{Red}{AB}}$ ya que B es el centro del círculo ACE Afirmación 4 y Definición D.15
7. ${\color{Red}{CA}}$ es igual a ${\color{Red}{CB}}$ Afirmación 5 y 6 y Noción común
8. Las tres rectas ${\color{Red}{CA}}$, ${\color{Red}{CB}}$ y ${\color{Red}{AB}}$ son iguales Afirmación 5,6 y 7
9.

El triángulo ${\color{Red}{ABC}}$ es equilátero

Es la Tesis que se debía demostrar

 Afirmación 8
Escribe las respuestas para recibir retroalimentación.
Teorema: Si dos rectas se cortan, hacen ángulos opuestos por el vértice iguales

Hipótesis. Dos rectas que se cortan (las rectas AB y GD se cortan en el punto E)

Tesis. Los ángulos opuestos por el vértice son iguales. (El ángulo ${\color{Red}{AEG}}$ es igual al ${\color{Blue}{GEB}}$, y el ${\color{Orange}{GEB}}$ al ${\color{Green}{AED}}$)

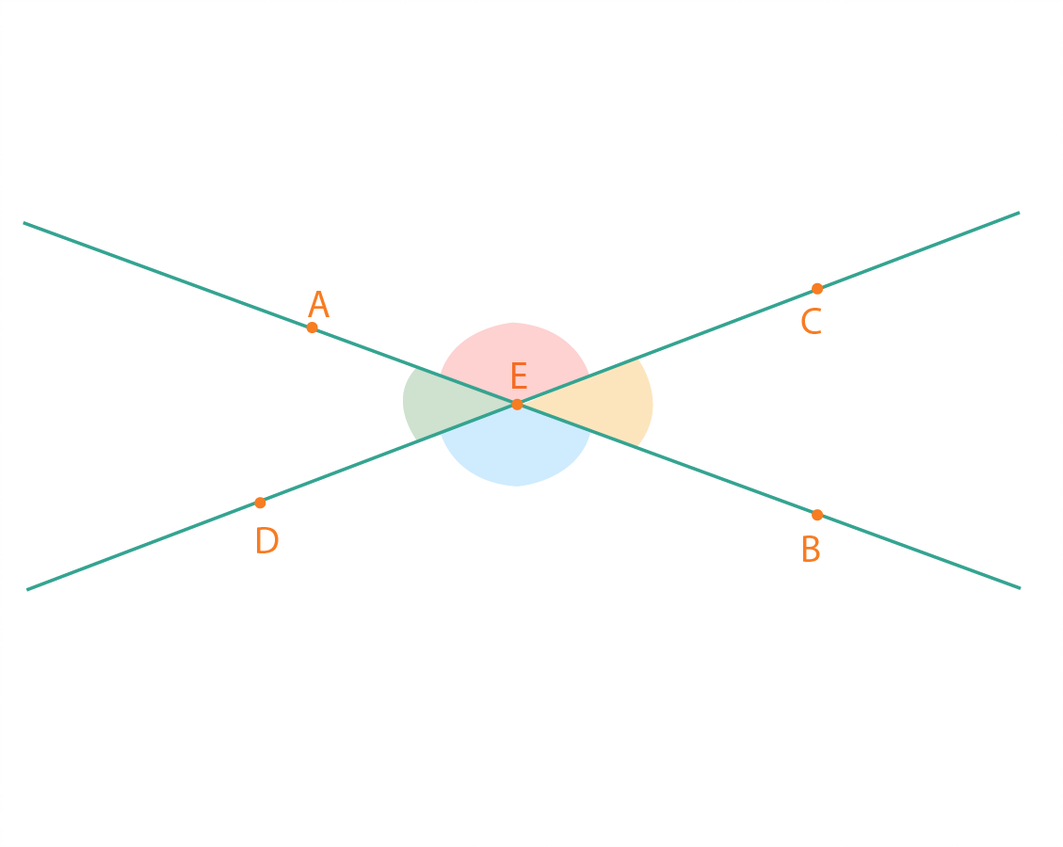
Proposición I.1 Teorema

Con base en la figura se describe cada paso de la demostración.

Razones utilizadas en la demostración de la Proposición I.15 :

Definición D.I.1 . Límite es lo que sea extremo de algo.

Proposición P.I.13.. Teorema: Si una recta levantada sobre otra hace ángulos, serán o bien dos rectos o bien igual a dos rectos.

Noción común N.1 . Las cosas que son iguales a una misma cosa son iguales entre sí.

Noción común N.1 . Si de cosas iguales se quitan otras iguales, las restantes son iguales.

Demostración

Afirmaciones Razones
1. La recta AE está levantada sobre la recta GD, hace los ángulos ${\color{Red}{GEA}}$ y ${\color{Green}{AED}}$ Hipótesis y Definición D.I.1
2. Los ángulos ${\color{Red}{GEA}}$, ${\color{Green}{AED}}$ son iguales a dos rectos Afirmación 1 y
3. La recta DE está levantada sobre AB hace los ángulos ${\color{Green}{AED}}$, ${\color{Blue}{DEB}}$ Hipótesis y Definición D.I.1
4. Los ángulos ${\color{Green}{AED}}$, ${\color{Blue}{DEB}}$ son iguales a dos rectos Afirmación 3 y
5. Los ángulos ${\color{Red}{GEA}}$, ${\color{Green}{AED}}$ son iguales a ${\color{Green}{AED}}$, ${\color{Blue}{DEB}}$ Afirmación 2 y 4 , Noción común N.1
6. Réstese el ángulo común ${\color{Green}{AED}}$ y se obtiene que los ángulos ${\color{Red}{GEA}}$ y ${\color{Blue}{DEB}}$ son iguales. Afirmación 5 y Noción común N.3
7. De manera parecida se demuestra que los ángulos ${\color{Yellow}{GEB}}$, ${\color{Green}{AED}}$ son iguales. Afirmación 1 a 6
8.

Los ángulos opuestos por el vértice son iguales. (El ángulo ${\color{Red}{AEG}}$ es igual al ${\color{Blue}{DEB}}$, y el ${\color{Orange}{GEB}}$ al ${\color{Green}{AED}}$)

Es la Tesis que se debía demostrar

 Afirmación 6 y 7

${\color{Red}{GEA}}+{\color{Green}{AED=180°}}$ (ángulos suplementarios)

${\color{Red}{BED}}+{\color{Green}{AED=180°}}$ (ángulos suplementarios)

${\color{Red}{GEA}}+{\color{Green}{AED=180°}}$ (Axioma. Dos cantidades iguales a un tercera son iguales entre sí)

${\color{Red}{GEA=BED}}$ (Axioma. Si a cantidades iguales les restas otras también iguales los totales son iguales).