A continuación, se presenta información en la que podrás observar contribuciones –aplicadas a problemas- de Thales de Mileto al desarrollo de la Geometría.
-
La Pirámide de Keops
Se dice que al preguntársele a Thales de Mileto cómo se puede calcular la altura de la pirámide del rey Khufu (pirámide de Keops), que ya tenía más de dos mil años de antigüedad en aquel tiempo, Thales explicó que aprovechando las sombras que produce la pirámide y su bastón al mismo tiempo.

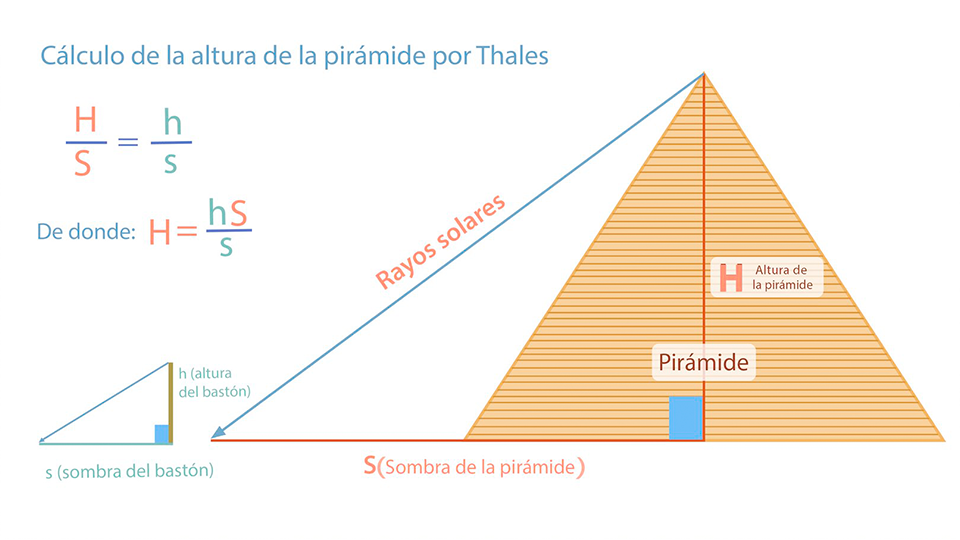
Considerando que el sol se encuentra muy lejos, los rayos del sol que inciden en la pirámide y en el bastón son paralelos, por lo que sus sombras determinan triángulos semejantes por tener iguales sus ángulos respectivos, como se muestra en la figura.
En los triángulos semejantes la razón entres sus lados correspondientes son iguales, por lo que se tiene que la altura de la pirámide entre la altura del bastón es igual a la longitud de la sombra de la pirámide entre la la longitud de la sombra del bastón:
$\frac{Altura\;de\;la\;pirámide}{Altura\;del\;bastón}=\frac{Longitud\;de\;la\;sombra\;de\;la\;pirámide}{Longitud\;de\;la\;sombra\;del\;bastón}$
Si a la hora que se hacen las medidas, la longitud de la sombra de la pirámide es 296.45 m, la sombra del bastón es 3.14 m. y la altura del bastón es de 1.45 metros, se tiene lo siguiente:
$\frac{Altura\;de\;la\;pirámide}{1.45\;m}=\frac{296.45\;m}{3.14\;m}$
De donde obtenemos:
$\tfrac{Altura\ de\ la\ piramide} = (\tfrac{296.45 m}{3.14 m} )({\color{black}{[1.45]}} m)) = {\color{black}{[136.89]}} m$
Por lo que la altura de la pirámide de Keops es 136.89 m.
-
Teorema 1 de Thales
Si la recta R es paralela al lado AB, entonces el triángulo ABC es semejante al triángulo DEC.
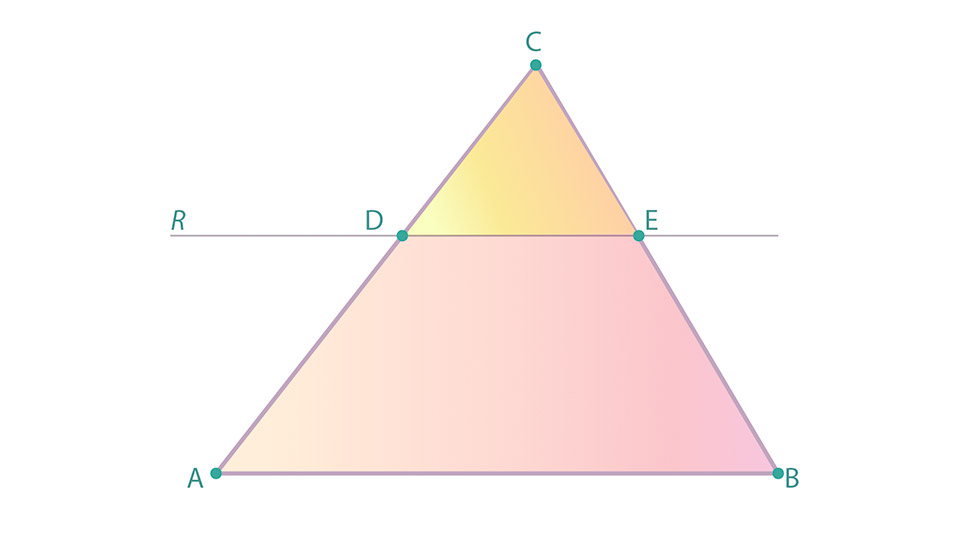 Dos triángulos son semejantes si tienen respectivamente sus ángulos iguales y sus lados proporcionales.
Dos triángulos son semejantes si tienen respectivamente sus ángulos iguales y sus lados proporcionales.Teorema 2 de Thales
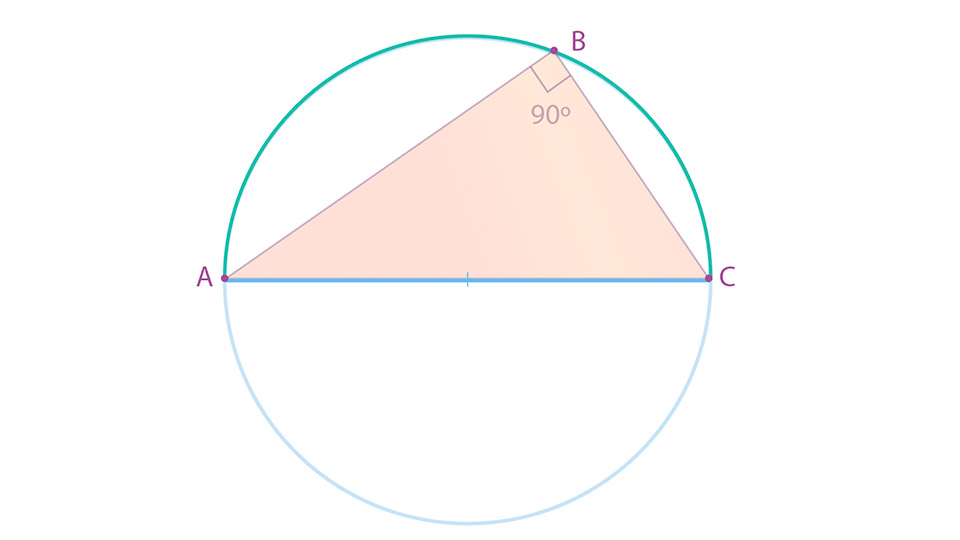
Si $B$ un punto de la circunferencia de diámetro $AC$, distinto de $A$ y de $C$. Entonces el triángulo $ABC$, es un triángulo rectángulo.
-
Aplicación del Teorema de Thales 2
Teorema 2 de Thales
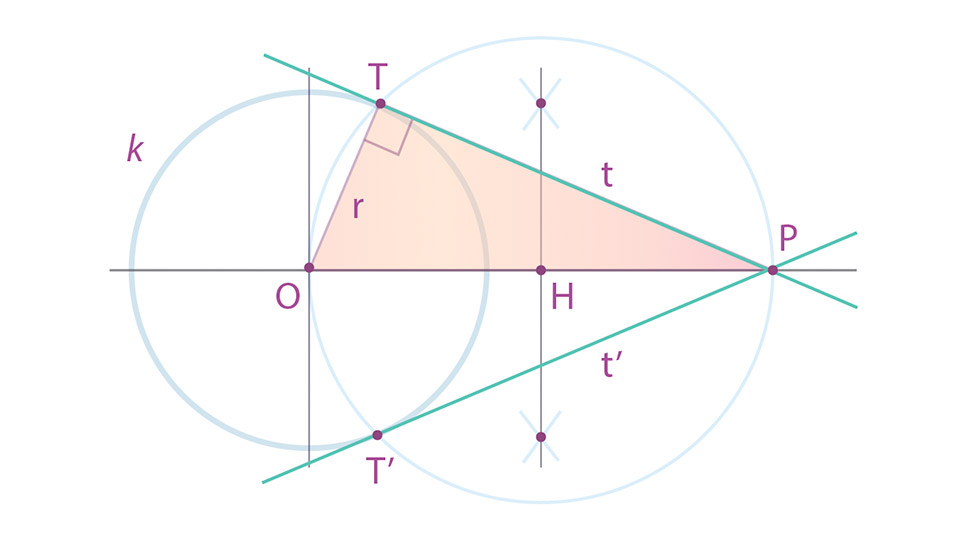
Construcción de tangentes (líneas rojas) a una circunferencia $k$ desde un punto $P$, utilizando el segundo teorema de Thales.
Justificación:
Tomando como base a la figura, el segundo teorema de Thales se puede aplicar para trazar las tangentes a una circunferencia $k$ dada, que pasen por un punto $P$ conocido y externo a la misma.
Por simetría cualquier radio $r$ de la circunferencia $k$ es perpendicular a la tangente del punto $T$ que dicho radio define en la misma, por lo que se concluye que ángulo $OTP$ es recto y el triángulo $OTP$ es rectángulo. Por el teorema 2 se puede deducir que el triángulo $OTP$ se inscribe en una circunferencia de radio $½$ de la hipotenusa $OP$ del mismo triángulo, como se observa en la figura.
Entonces marcando el punto $H$ como punto medio de la hipotenusa $OP$ y haciendo centro en el mismo, podemos dibujar una segunda circunferencia auxiliar (gris en la figura) que será la que circunscribe al triángulo $OTP$.
Esta última circunferencia trazada se intersecará con la circunferencia $k$ en dos puntos $T$ y $T'$, que son justamente los puntos de tangencia de las dos rectas que tangentes a la circunferencia $k$ y pasan por el punto $P$. Ya conocidos los puntos $T$ y $T'$ solo se trazan las rectas $TP$ y $T'P$ (rojas en la figura) que son tangentes a la circunferencia original.


