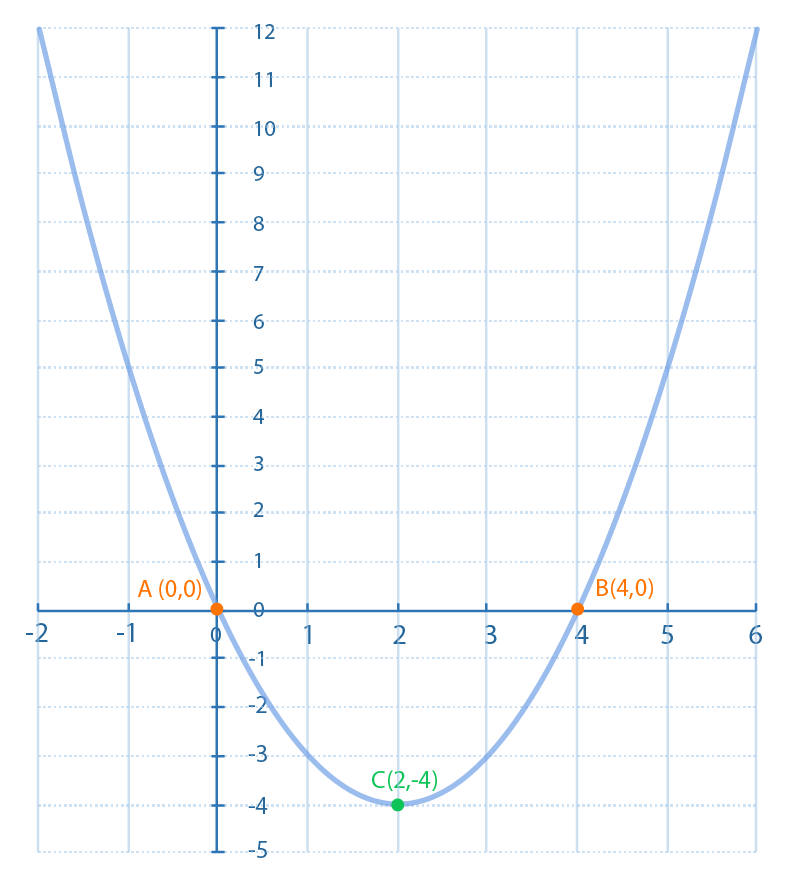
Para facilitar la obtención de los elementos de la función cuadrática se requiere pasar de la función cuadrática de la forma general $y=ax^2+bx+c$ a la forma estándar $y=a(x-h)^2+k$. En el siguiente ejemplo se proporciona la función cuadrática en su forma general y los procesos algebraicos para obtener la forma estándar.
Recuerda que en la forma estándar $y={\color{blue}{a}}(x-{\color{Orange}{h}})^2+{\color{Purple}{k}}$.
- ${\color{blue}{a}}$ determina la concavidad de la función:
- ${\color{blue}{a>0}}$: hacia arriba.
- ${\color{blue}{a<0}}$: hacia abajo.
- En ${\color{Orange}{x=h}}$ se ubica el eje de simetría.
- En ${\color{Purple}{y=k}}$ se ubica la ordenada donde cambia de sentido la gráfica.
- El vértice de la parábola se ubica en $C({\color{Orange}{h}},{\color{Purple}{k}})$.
Si necesitas conocer o repasar este tema consulta cómo obtener la Forma estándar en el estudio de la función cuadrática.
Deducir la forma estándar de la función cuadrática especificar los elementos de la función $y=2x^2+4x-6$, que se obtiene al agrupar la variable $x$.
Completa el trinomio cuadrado perfecto en $x$, sumando y restando el cuadrado de la mitad del coeficiente del término lineal.
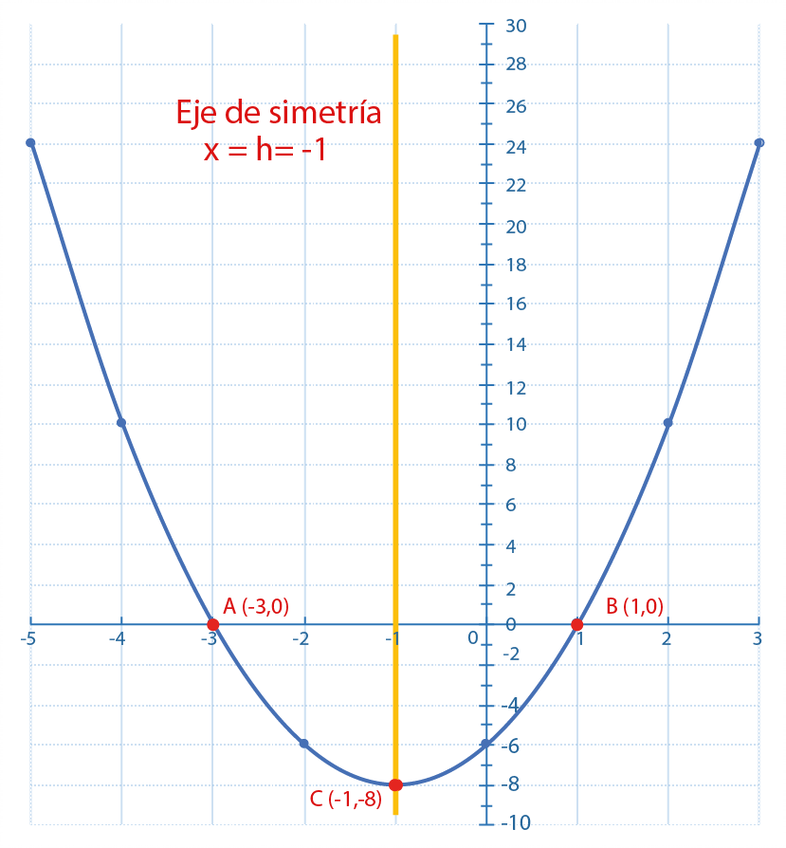
De la función cuadrática en su forma estándar se obtienen los elementos de la función cuadrática como se indica, completa en los recuadros la información faltante.
Fin de la actividad
A partir de las siguientes funciones, utilizarás las representaciones de la forma general y estándar para obtener los parámetros de la gráfica de la función de segundo grado: los ceros de la función y el vértice de la parábola.
Revisa el siguiente fichero, la primera ficha contiene un ejemplo de cómo calcular los parámetros de la representación gráfica de la función de segundo grado: a partir de la forma general $y=ax^2+bx+c$ (igualándola a cero y utilizando la formula general de la ecuación de segundo grado), puedes calcular los ceros o raíces de la función; mientras que con la forma estándar $y=a(x-h)^2+k$ puedes ubicar el eje de simetría y el punto dónde la función tiene un máximo o un mínimo.
Si requieres repasar como cambiar entre ambas representaciones, consulta: Deducción de la forma estándar a partir de la forma general y Deducción de la forma general a partir de la forma estándar.
Con base en la función $y=\tfrac{1}{2}x^2-10x+42$. Determina la forma estándar e identifica sus elementos:
Con base en la función $y = -\tfrac {1}{2}x^2 + 5x - \tfrac{9}{2}$. Determina la forma estándar e identifica sus elementos:
- Concavidad de la función.
- Coordenadas del vértice.
- Eje de simetría.
- Ceros de la función.
A partir de la forma general: $y=ax^2+bx+c$ se obtiene la forma
estándar: $y=a(x-h)^2+k$
Al igualar la función cuadrática se obtienen los ceros de la función, puedes ocupar cualquiera de las dos formas, la que te resulte más simple, aunque se recomienda utilizar la función estándar. el eje de simetría se ubica en $x=h$
el punto máximo o mínimo se ubica en el vértice de la parábola $C(h,k)$
El parámetro a, indica la concavidad de la función:
La concavidad de la función es hacia arriba
La función tiene un mínimo con $x=h$ y $y=k$
El rango de la función es $[k,∞)$
La concavidad de la función es hacia arriba
La función tiene un mínimo con $x=h$ y $y=k$
El rango de la función es $[k,∞)$
Fin de la actividad