Problemas de aplicación

Geogebra

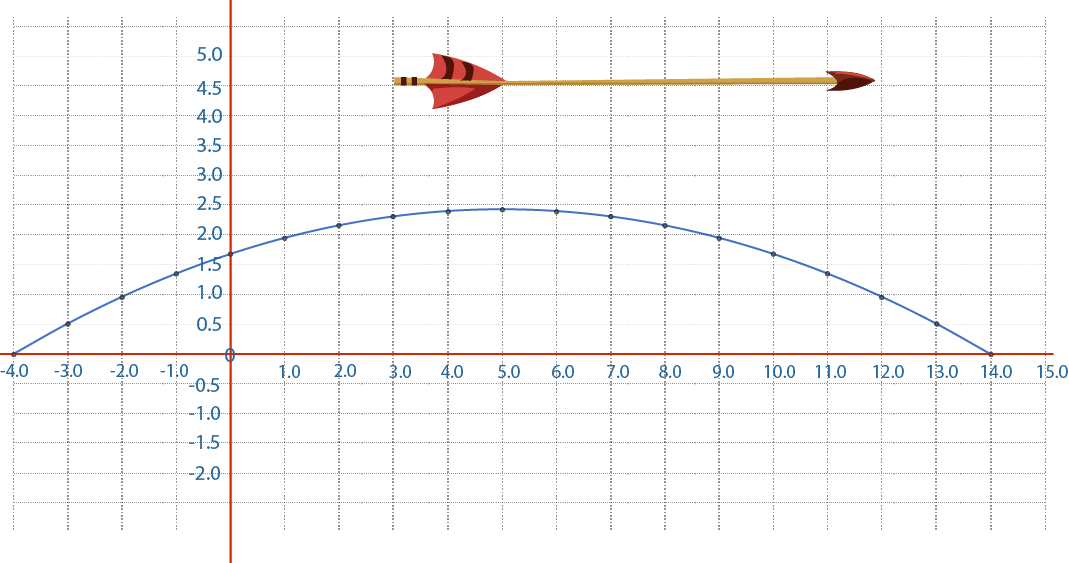
La trayectoria de una flecha lanzada con un arco a una altura de 1.68 m puede ser representada por la función cuadrática $y=-0.03x^2 + 0.3x + 1.68$ ,donde $x$ es la distancia horizontal recorrida que varía desde cero hasta que cae, $y$ representa la altura, tanto distancia como altura están en metros.

¿Qué tan lejos y alto llegará la flecha?

El lanzamiento termina cuando la flecha lanzada cae al suelo.

Geogebra

Problema El Arquero

El recurso Geogebra te permitirá la exploración y visualización de la trayectoria del lanzamiento de la flecha.

Ejercicio de escritura

Ahora que ya revisaste el recurso, contesta las siguientes preguntas:

Esquema
  1. Altura de la flecha al inicio del movimiento:
    1.68 m
  2. Altura cuando llega al suelo:
    0 m
  3. Altura máxima de la trayectoria:
    2.43 m
  4. Determina el alcance de la flecha:
    14 m

Retroalimentación: 1

$y$ $=-0.03x^2 + 0.3x + 1.68$

$y({\color{Red} 0})$ $=-0.03({\color{Red} 0})^2 + 0.3({\color{Red} 0}) + 1.68$

$={\color{Gray} 0+0+}1.68$

$=1.68$

Retroalimentación: 3

Con base en la función cuadrática en su forma estándar $y=-0.03(x-5)^2+2.43$, la altura es $k=2.43$

Retroalimentación: 4

  • 1 La posición de la flecha está dada por la función cuadrática en su forma estándar: $y=-0.03(x-5)^2+2.43$
    2 para que la flecha llegue al suelo se requiera que la altura $y=0$, por lo que se obtiene la ecuación:

    $-0.03(x-5)^2+2.43=0$
    3 Al transponer el termino cuadrático al lado derecho de la ecuación Y dividir los lados de la ecuación por 0.03 resulta:

    $2.43=0.03(x-5)^2$

    $(x-5)^2=\tfrac{2.43}{0.03}$
    4 Simplificando:

    $(x-5)^2=81$
    5 Al extraer la raíz cuadrada a los lados de la ecuación resulta:

    $\sqrt{(x-5)^2}=\sqrt{81}$
    6 se obtiene la ecuación

    $x-5=\pm 9$

    $x=5 \pm 9$
  • 1 La posición inicial del disparo de la flecha es $(0, 1.68)$. La posición de la flecha está dada por la función: $y=-0.03x=-0.03x^2+0.30x+1.68$
    2 para que la flecha llegue al suelo se requiera que la altura y sea cero, por lo que se obtiene la ecuación:

    $-0.03x^2+0.30x+1.68$
    3 Utilizando la fórmula general:

    $x=\frac { -b \pm \sqrt{b^2-4ac} }{2a}$
    4 Ubica los parámetros:

    $a=-0.03 b=0.3 c=1.68:$
    5 Sustituyendo valores:

    $x=\frac { -0.3 \pm \sqrt{(0.3)^2-4(-0.03)(1.68)}}{2(-0.03)}$
    6 Simplificando

    $x=\frac { -0.3 \pm \sqrt{0.09+0.2016}}{-0.06}$

    $x=\frac { -0.3 \pm \sqrt{0.2916}}{-0.06}=\frac { -0.3 \pm 0.54}{-0.06}$
    7

    $x=\frac { -0.3 - 0.54}{-0.06}=\frac { -0.84}{-0.06}$

    $x=\frac { -0.3 + 0.54}{-0.06}=\frac { 0.24}{-0.06}$

y al resolverla se determinan las raíces:

$x_1=14$

$x_2=-4$

de éstas, la raíz $x_2=-4$ no tiene sentido en el contexto del problema, por lo que el alcance de la flecha es de $x_2=14$. La parábola descrita por la función cuadrática tiene dos intersecciones en $x$. Pero el tiro sólo viajó sobre parte de esa curva. La solución, -4, no puede ser la distancia recorrida porque es un número negativo.

El lanzamiento de la flecha llega hasta $x = 14m$, ya que cuando llega al suelo $y=0$.

Debes escribir tu respuesta para recibir retroalimentación.