Para el desarrollo del tema problemas de aplicación que involucran a las funciones cuadráticas, como punto de partida se presenta a los alumnos conceptos básicos relacionados con este tipo de funciones y su gráfica que corresponde a una parábola, puesto que estos conceptos son esenciales para la resolución de problemas en diversos contextos. Los conceptos abordados tienen que ver con la concavidad de la parábola, eje de simetría, máximos y mínimos de funciones, así como, los ceros de la función cuadrática. Para su estudio se les presentan actividades de aprendizaje para la identificación de los conceptos mencionados, para después pasar al planteamiento y solución de problemas en diversos contextos de su entorno.
Las trayectorias de los objetos celestes, como las órbitas que describen los cometas se clasifican en tres familias de cónicas: elípticas, parabólicas e hiperbólicas. En este material se abordarán únicamente las funciones de segundo grado, cuya representación son parábolas.
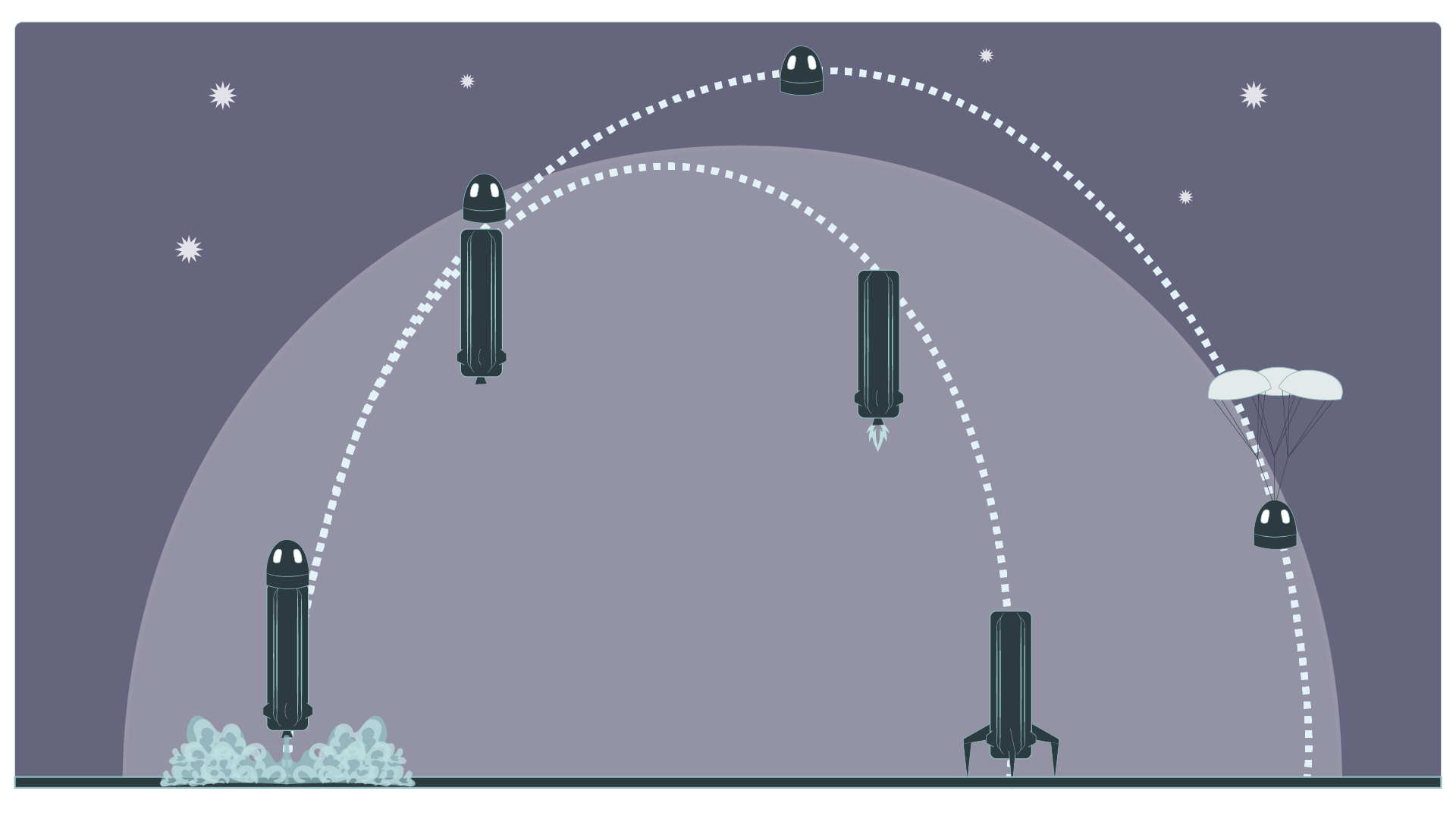
Lanzamiento de objetos. Cuando se lanza un objeto, como una pelota o un proyectil, éste describe la trayectoria que puede modelarse como una parábola o una función de segundo grado. El movimiento en el eje horizontal se realiza de manera lineal; mientras que la altura en el eje vertical puede modelarse con funciones de segundo grado a lo largo del recorrido. El estudio de los diferentes tipos de movimiento se utiliza en la Física.
El siguiente video muestra la trayectoria que sigue una pelota golpeada por el bateador. Se coloca una gráfica donde se muestran los elementos básicos de la función cuadrática, los cuales revisarás más adelante.
Con este material resolverás problemas de optimización con métodos algebraicos a partir de situaciones que varían en forma cuadrática a fin de continuar con el estudio de las funciones.


