Actividad Final - Problemas aplicando la función cuadrática

Características de una función cuadrática

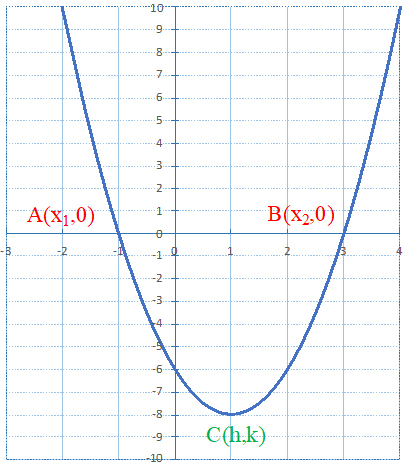
Determina el máximo o mínimo de la función $y=2x^2-4x-6$.
Luego grafica la función en tu cuaderno de notas con cualquiera de los métodos que conozcas y compara con la mostrada en la figura.

Tip: recuerda obtener la representación en la forma estándar.

Ejercicio de escritura
a) Concavidad de la parábola:
Hacia arriba. La parábola abre hacia arriba ya que el coeficiente del término cuadrático es positivo, por lo tanto, es positiva.
b) Coordenadas del vértice $C=$

( , )

$C= (1,-8)$

$y=2x^2-4x -6$
$y=2(x^2-2x)-6 $
$y=2x^2-2x+1-1-6$
$y=2(x^2-2x+1)-6-2$
$y=2(x-1)^2-8$
c) La ecuación del eje de simetría $x=$

$x=1$

A partir de la forma estándar se obtiene el eje de simetría, recuerda que el vértice de una función cuadrática se ubica en $C(h,k)$.
d) Los ceros de la función

$x_1=$ y $x_2=$

$x_1=-1 y x_2=3$

Igualando a $0$ la función tenemos…:

$y=2(x-1)^2-8=0$
$2(x-1)^2=8$
$(x-1)^2=4$
$x-1=\pm\sqrt{4}$
$x=1\pm 2$
$x_1=-1 y x_2=3$
e) El valor mínimo de la función es:

$-8$

A partir de la forma estándar, el eje de simetría se ubica en x=h. Por lo que el rango de la función es$[-8,+\infty)$
Debes escribir tu respuesta para recibir retroalimentación.

Área de pastura

Un ejido dedicado a la ganadería requiere disponer de un terreno rectangular a fin de producir la pastura necesaria para alimentar a su ganado. Para mantener separado a los animales del pastizal mientras está en condiciones óptimas de ser aprovechado necesita ser cercado. Si sólo dispone de 800 metros de cerca, pero puede utilizar una cerca larga ya construida por el ejido vecino como uno de los lados del terreno, ¿cuáles son las dimensiones del terreno de mayor área posible que se pudiese cercar y el área máxima?

Geogebra
Geogebra

El modelo geométrico asociado al problema lo puedes consultar en el GeoGebra "Cerca del ejido vecino ya construida".

Ejercicio de checkbox

De los parámetros de la función cuadrática, indica cual nos indicaría la solución del máximo valor del área:

Ejercicio de escritura
Función asociada al área: $Área=(largo)(ancho)$
simplificando: $a(x)=$ $x^2+$ $x$

$a(x)=-1x^2+400x$
$área = (ancho)(altura) $
$a(x) = x (400-x) $
$a(x) = –x2+400x $
Área máxima : $m^2$

Obteniendo la forma estándar de la ecuación:

$a(x)=–x^2+400x $
$a(x)=-(x^2-400x)$
$a(x)=-(x^2-400+200^2-200^2)$
$a(x)=-(x^2-400x+40000)+40000$
$a(x)=-(x-{\color{orange}200})^2+{\color{purple}40000}$
Valor del largo para el área máxima:

$m^2$

De la forma estándar $a(x)=-(x-{\color{orange}200})^2+40000$

Valor del ancho para el área máxima:

$m^2$

De la forma estánda $largo=400-x=400-200=200$

Clavadista

En el instante $t=0$ segundos un saltador se lanza desde un trampolín que está a $32 pies$ de la alberca y describe la altura que alcazanza en el clavadista en cada momento con la función $s(t)=-16t^2+16t+32$. Considera que la alberca se ubica en $altura=0$ y determina lo que se te pide:

Ejercicio de escritura
Altura máxima alcanzada por el saltador $pies$

$36pies$

Función cuadrática $s(t)=-16t^2+16t+32$
Factorizar el valor numérico de los términos cuadrático y lineal. $s(t)=-16(t^2+t)+32$
Completar el trinomio cuadrado perfecto en x, sumando y restando el cuadrado de la mitad del coeficiente del término lineal. $s(t)=-16(t^2-t+\tfrac{1}{4}-\tfrac{1}{4})+32$
Agrupando el trinomio cuadrado perfecto se obtiene. $s(t)=-16(t^2-t+\tfrac{1}{4})+32+4$
Factorizando el trinomio cuadrado perfecto resulta la función estándar. $s(t)=-16(t-\tfrac{1}{2})^2+36$

Ahora como la función cuadrática está en su forma estándar las coordenadas del vértice son $V(\tfrac{1}{4},36)$ y como la parábola se abre hacia abajo, la máxima altura que alcanza el saltador es $k=36$ pulgadas.
Tiempo utilizado por el saltador para obtener la altura máxima $seg$

De la forma estándar: $s(t)=-16(t-{\tfrac{1}{2}})^2+36$, $t=0.5seg$.
Tiempo utilizado por el saltador para que se ubique a una altura de 32 pies sobre la alberca

$0 y$ $seg$

Al iniciar el brinco y regresar desde la parte más alta alcanzada. El tiempo que utiliza el saltador para recorrer una distancia de $32$ pies, se obtiene al resolver la función igualada a cero, tal como se presenta en la tabla.

Función cuadrática se iguala a 32 $-16(t-\tfrac{1}{2})^2+36=32$
Transponer el término constante del lado izquierdo al derecho de la ecuación y simplificar. $-16(t-\tfrac{1}{2})^2=32-36=-4$
Transponer el factor término constante del lado izquierdo al derecho de la ecuación y simplificar. $ (t-\tfrac{1}{2})^2=\tfrac{1}{4}$
Extraer raíz cuadrada a los lados de la ecuación. $t-\tfrac{1}{2}=\pm\tfrac{1}{2}$
Resolviendo la ecuación se obtiene el tiempo solicitado. $t_1=0 y t_2=1$
Tiempo que tarda el saltador en llegar al agua

$seg$

De manera similar se resuelve la ecuación para determinar el tiempo que utiliza el saltador para llegar al agua.

Función cuadrática se iguala a $0$ $-16(t-\tfrac{1}{2})^2+36=0$
Transponer el término constante del lado izquierdo al derecho de la ecuación y simplificar. $-16(t-\tfrac{1}{2})^2=-36$
Transponer el factor constante del trinomio cuadrado perfecto del lado izquierdo al derecho de la ecuación y simplificar. $(t-\tfrac{1}{2})^2= \tfrac{9}{4}$
Extraer raíz cuadrada a los lados de la ecuación. $t-\tfrac{1}{2}=\pm\tfrac{3}{2}$
Resolviendo la ecuación se obtiene el tiempo solicitado. $t_1=-1 y t_2=2$

Se descarta $t_1=-1$ puesto que no tiene sentido en el contexto del problema por lo que t_2=es el tiempo utilizado por el saltador para llegar al agua.

Coreback

La trayectoria de un ovoide que es lanzado por el coreback a una altura de 1.5 m puede ser representada por la función cuadrática $y=0.008x^2+0.36x+1.5$, donde $x$ es la distancia horizontal recorrida que varía desde cero hasta que es atrapada por el receptor a la misma altura del lanzamiento, y representa la altura, tanto distancia como altura están en metros. ¿Qué tan alto y lejos llegará el ovoide?

Ejercicio de checkbox

De los parámetros de la función cuadrática, indica cual nos indicaría la solución del máximo valor del área:

Ejercicio de escritura

Altura máxima a la que llegará el balón:$m$

Que tan lejos llegará el balón:$m$

Función cuadrática $y=-0.008x^2+0.36x+1.5$
Factorizar los factores numéricos $y=-\tfrac{1}{125} \left( x^2-45x+\tfrac{2025}{4}-\tfrac{2025}{4} \right) +\tfrac{3}{2}$
Agrupando el trinomio cuadrado perfecto $y=-\tfrac{1}{125} \left( x^2-45x+\tfrac{2025}{4} \right) +\tfrac{3}{2}+\tfrac{81}{20}$
  $y=-\tfrac{1}{125} \left( x-{\tfrac{45}{2}} \right) + {\tfrac{111}{20}}$
$y=-0.008 \left( x-{\color{orange}22.5} \right) + {\color{purple}5.55}$