En concordancia con el teorema fundamental del cálculo la integral definida de la función $f(x)$ se obtiene con la expresión $\int_{a}^{b}f(x) dx=F(x)]_{a}^{b}=F(b)-F(a)$, en la cual, $a$ y $b$ son los límites de integración inferior y superior, respectivamente. En consecuencia, la integral definida resulta ser un número, mientras que la integral indefinida $\int f(x) dx=F(x)+C$, resulta ser una familia de funciones. Es importante señalar que el teorema mencionado relaciona a la integral definida con la integral indefinida, puesto que en ambas la función $F(x)$ es la antiderivada de la función puesto que , tal como, lo puedes comprobar con tu interacción con el recurso GeoGebra y con la integral indefinida.

Revisa e interactua el siguiente recurso GeoGebra Integral definida vs integral indefinida
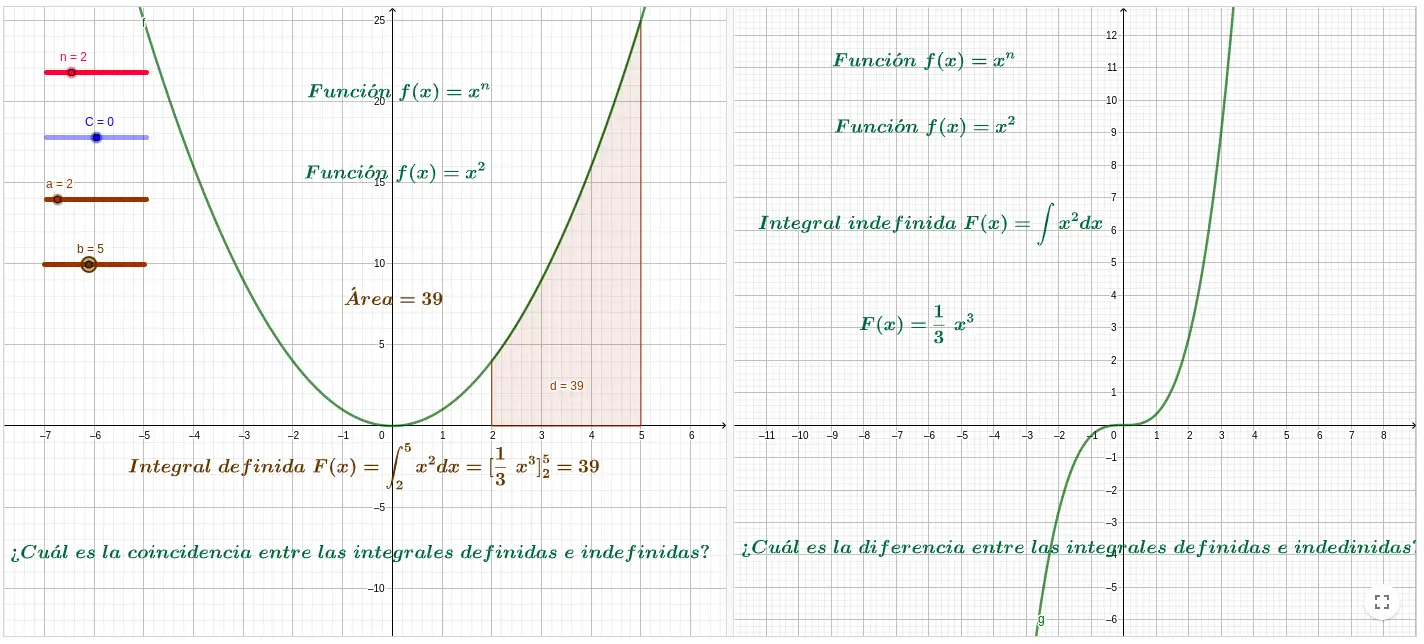
Con base en tu interacción con el recurso GeoGebra, completa la frase para que la afirmación sea correcta.
Procedimientos algebraicos para la obtención de ambas integrales.
| Integral indefinida | Integral definida |
|---|---|
| $\int x^2 dx = \frac{1}{3} x^3+C$ | $\int_{1}^{4}x^2 dx = [\frac{1}{3} x^3 ]_1^4=\frac{1}{3} (4)^3-\frac{1}{3} (1)^3=21$ |
Ahora se te plantea un ejercicio que te permitirá consolidar las similitudes y diferencias relacionadas con la integra definida e indefinida.
Ejercicio 1. Determina la integral definida y la indefinida que se especifica en la tabla
Con este ejercicio, obtendrás las integrales indefinida y definida, las cuales te permitirán la comprensión de sus similitudes y deferencias.
Arrastra los valores al lugar que corresponde en la tabla.
| Integral indefinida | Integral definida |
|---|---|
| $\int x^2 dx = \frac{1}3{} x^3+C$ | $\int_{2}^{5}x^2 dx =\left [ \frac{1}{3}x^{3} \right ]_{2}^{5}=\frac{1}{3} (5)^3-\frac{1}{3} (2)^3=39$ |
Como conclusión podemos mencionar que la resolución de problemas que involucran la integral definida se requiere la obtención de la integral indefinida, tal como, lo ilustran los ejemplos siguientes.
Ejemplo 1.
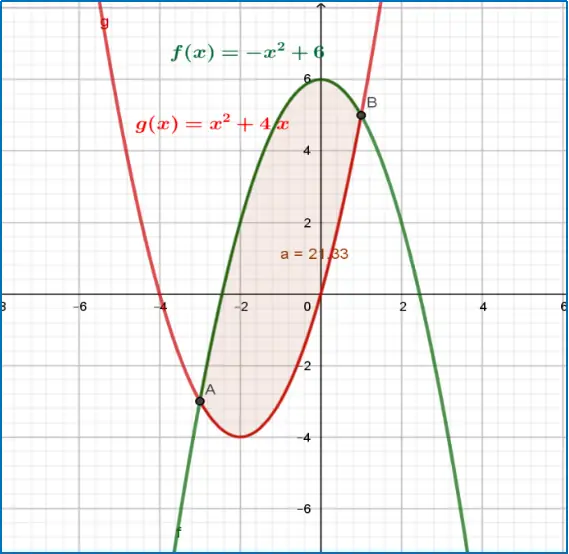
Con base en la gráfica de las funciones $f(x)=-x^2+6$ y $g(x)=x^2+4x$, calcula el área de la región limitada por ambas funciones.
Solución
El área de la región acotada se obtiene con la integral indefinida y posteriormente el uso de la integral definida, tal como, lo muestran los siguientes procedimientos algebraicos.
$Área = \int_{-3}^{1}[f(x)-g(x)]dx = \int_{-3}^{1}[(-x^2+6)-(x^2+4x)]dx = -4x+6 dx=$
$\int_{-3}^{1}(-2x^2-4x+6) dx=\left [ -\frac{2}{3} x^3-2x^2+6x\right ]_{-3}^{1}$
$=\left [ -\frac{2}{3} (1)^3-2(1)^2+6(1) \right ]-\left [ -\frac{2}{3} (-3)^3-2(-3)^2+6(-3)\right ]=$
$\left [-\frac{2}{3}-2+6\right ]-\left [ 18-18-18\right ]=-\frac{2}{3}+4+18=\frac{64}{3}$ unidades cuadradas.
Ejemplo 2.
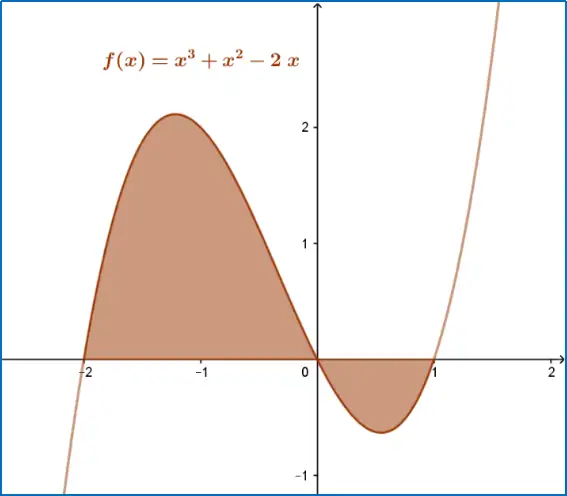
Con base en la gráfica de la función $f(x)=x^3+x^2-2x$ determina el área de la región sombreada.
Solución
El área de la región se obtiene con la integral indefinida y después con la integral definida de la parte positiva menos la de la parte negativa, tal como, lo ilustran los siguientes procedimientos algebraicos.
$Área = \int_{-2}^{0}(x^3+x^2-2x)dx-\int_{0}^{1}(x^3+x^2-2x)dx =$
$ \left [ \frac{1}{4} x^4+\frac{1}{3} x^3-x^2\right ]_{-2}^{0}= \left [ \frac{1}{4} (0)^4+\frac{1}{3} (0)^3-(0)^2\right ] -\left [ \frac{1}{4} (-2)^4+\frac{1}{3} (-2)^3-(-2)^2\right ]=$
$-4+\frac{8}{3}+4=\frac{8}{3}$ evaluación del área positiva.
$\left [ \frac{1}{4} x^4+\frac{1}{3} x^3-x^2 \right ]_{0}^{1} =\left [ \frac{1}{4} (1)^4+\frac{1}{3} (1)^3-(1)^2 \right ]-\left [ \frac{1}{4} (0)^4+\frac{1}{3} (0)^3-(0)^2 \right ]= $
$\frac{1}{4}+\frac{1}{3}-1=-\frac{5}{12}$, evaluación del área negativa.
$\dot{A}rea\ sombreada=\frac{8}{3}-\left ( -\frac{5}{12} \right )=\frac{8}{3}+\frac{5}{12}=\frac{37}{12}$