En concordancia con el estudio del Cálculo integral, la integral definida se define como el límite de las sumas de Riemann para el cálculo del área de la región acotada de la función continua $f$ en el intervalo $[a,b]$, representada como $$\lim_{\Delta x\rightarrow 0}\sum_{i=1}^{n}f(x_{i})\Delta x)=\int_{a}^{b}f(x)dx=F(x)]_{a}^{b}=F(b)-F(a)$$ donde $\Delta x=\frac{b-a}{n}$ es la base de cada rectángulo con una partición del intervalo en $n$ partes iguales, $f(x_i)$ es la altura del rectángulo $i -$ ésimo y $f(x_i)\Delta x$ su área; el siguiente esquema ilustra la definición de la integral definida:
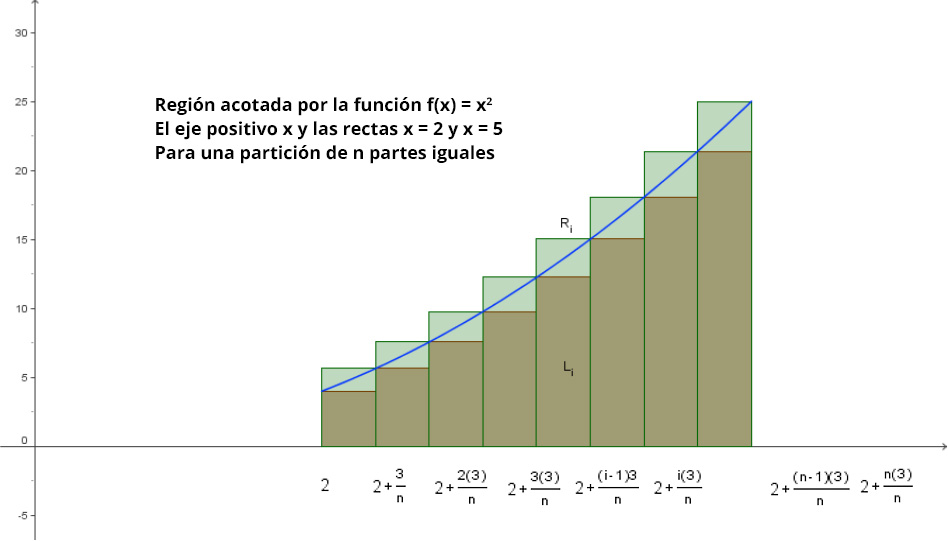
Área =$\lim_{n \to \infty }\left ( 39-\frac{63}{2n}+\frac{9}{2n^{2}} \right )=39$
Área =$\int_{2}^{5}x^{2}dx=\left [ \frac{x^{3}}{3} \right ]_{2}^{5}=\frac{125}{3}-\frac{8}{3}=\frac{117}{3}=39$ unidades cuadradas
Ahora cuando la función es positiva la integral definida se interpreta geométricamente como el área comprendida por la función, el $Eje$ $x$ y las rectas $x=a$ y $x=b$, para obtener la integral se aplica el teorema fundamental del cálculo en el intervalo mencionado; es decir, $\int_{a}^{b}f(x)dx=F(b)-F(a)$, en la que $F$ es una antiderivada de $f$. Cabe mencionar que esta definición es un caso particular de la integral definida de Riemann, ya que considera rectángulos inscritos y circunscritos de igual base.
Para ilustrar su aplicación, determinemos el área de la región acotada por la función continua $f(x)=x^2+1$, el Eje $x$ y las rectas $x=-2$ y $x=5$, el área a determinar se muestra en la figura.
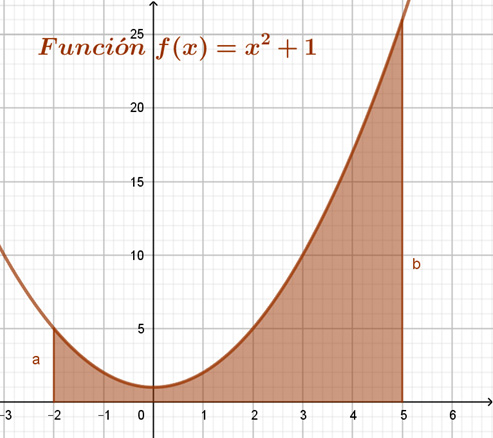
Área =$\int_{-2}^{5}f(x)dx=\int_{-2}^{5}(x^2+1)dx=\left [ \color{red}{\frac{x^{3}}{3}+x} \right ]_{-2}^{5}=\left [\frac{(5)^{3}}{3}+5 \right ]-\left [\frac{(-2)^{3}}{3}+(-2) \right ]=\frac{125}{3}+5+\frac{8}{3}+2=\frac{133}{3}+7=\frac{154}{3}$ unidades cuadradas; lo importante de la aplicación del Teorema fundamental del cálculo consiste en buscar una función cuya derivada sea la función original y evaluarla en los límites de integración, en el ejemplo, dicha función es la de color rojo y la representamos con $F(x)=\frac{x^{3}}{3}+x$, ya que $F'(x)=x^2+1=f(x)$. La función $F$ es una antiderivada de la función $f$ y se obtiene con el proceso inverso de la derivación: la integración de funciones.
En este material se estudiarán la integración inmediata y los métodos de integración: cambio de variable y la integración por partes para la obtención de la antiderivada de funciones, así como, su aplicación en la resolución de problemas en diversos contextos. Para ello, se requiere que utilices tus aprendizajes, habilidades y destrezas obtenidas en la aplicación de las reglas de derivación para funciones algebraicas y trascendentes que faciliten la integración de funciones.
Con lo anteriormente señalado el proceso de integración es la operación inversa de la diferenciación y consiste en la búsqueda de una función $F(x)$, tal que su derivada sea la función dada $f(x)$, es decir, $F'(x)=f(x)$. La solución general es de la forma $F(x)+C$, en ésta la función $F(x)$ es la antiderivada de la función $f(x)$ y se representa con la notación matemática:
$$\int f(x)dx=F(x)+C$$
El símbolo $\int$ fue inventado por Leibniz debido a que la integral es el límite de las sumas infinitas de rectángulos inscritos y circunscritos para determinar área de regiones acotadas, en esta expresión $f(x)$ es el integrando, $C$ es la constante de integración, el símbolo $dx$ indica que $x$ es la variable que se utiliza en el proceso inverso de la diferenciación y es la variable de integración; más adelante le daremos un significado más formal como la diferencial de la variable independiente. Los siguientes ejemplos muestran su aplicación.
Selecciona la respuesta correcta de los siguiente ejemplos.
Ejemplo 1. Obtén la antiderivada de la función $f(x)=2x$ que pase por el origen.
Solución busquemos una función $F(x)$ que tenga como derivada la función dada y que cumpla con la condición establecida, con base al aprendizaje que lograste sobre la obtención de la derivada de funciones algebraicas, elige la antiderivada pedida:
Ejemplo 2. Calcula la antiderivada de la función $f(x)=cos(x)$ que pase por el origen.
Solución busca una función $F(x)$ que tenga como derivada la función dada y que cumpla con la condición especificada, con base en el aprendizaje que lograste sobre la obtención de la derivada de funciones trigonométricas, elige la antiderivada pedida:
Ejemplo 3. Determina la antiderivada de la función $f(x)=e^{2x}$ que pase por el punto $\left ( 0,\frac{1}{2} \right )$
Solución busca una función $F(x)$ que tenga como derivada la función dada y que satisfaga la condición especificada, con base en el aprendizaje que lograste sobre la obtención de la derivada de funciones exponenciales, elige la antiderivada pedida:
Ejemplo 4. Determinar la antiderivada de la función $f(x)=\frac{1}{x+1}$ que pase por el origen.
Solución busca una función $F(x)$ que tenga como derivada la función dada y que pase por el origen, con base en el aprendizaje que lograste sobre la obtención de la derivada de funciones logarítmicas, elige la antiderivada pedida:
Ejemplo 5. Determinar la antiderivada de la función $f(x)=5x^3$ que pase por el origen.
Solución obtén una función $F(x)$ que tenga como derivada la función dada y que pase por el origen, con base en el aprendizaje que lograste sobre la obtención de la derivada de funciones algebraicas, elige la antiderivada solicitada:


