Actividad final

En este apartado utilizarás los aprendizajes que lograste sobre la integral indefinida, su relación con la integral definida, la integración inmediata de funciones, los métodos de integración (cambio de variable y la integración por partes), así como, su aplicación en la resolución de problemas en diversos contextos.

Para ello, resuelve los problemas propuestos aplicando el método de integración correspondiente y presta atención a los que involucran condiciones iniciales, así como, aquello que requieren del teorema fundamental del cálculo.

Problemas que involucran condición inicial

Arrastrar

Arrastra los valores donde corresponda en cada uno de los problemas.

Problema 1. Se lanza una piedra directamente hacia abajo desde una altura de 96 pies con una velocidad inicial de $16\ \frac{pies}{s}$. Determina:

$-80\ \frac{pies}{s}$

$s(t)=-16t^2-16t+96$

$t=2$

$v(t)=-32t-16$

La función velocidad.
La función de posición a los $t$ segundos.
El momento en que llegará al suelo.
La velocidad con la que llega al suelo.

Los procedimientos utilizados en la resolución del problema se presentan a continuación:

Problema 2. Se lanza verticalmente un paracaidista desde un helicóptero con una velocidad inicial de $(192\ \frac{pies}{s}$ desde una altura 346 pies. Determina:

$t=1.5s$

$-32t-192$

$-224\ \frac{pies}{s}$

$-240\ \frac{pies}{s}$

$-16t^2-192t+346$

La función velocidad.
La función de posición.
Tiempo utilizado por el paracaidista al llegar suelo
La velocidad del paracaidista al llegar al suelo.
La velocidad que llevaba el paracaidista al segundo de haber iniciado el descenso.

Aplicando los procedimientos algebraicos para este tipo de problemas se obtiene la solución del problema, tal como, se presenta en seguida:

Aplicación de los métodos de integración

Determina las integrales que se indican aplicando el método de integración, según corresponda (integración inmediata, integración por sustitución o integración por partes).

$-\frac{1}{3} cos x^3+C$

$\frac{2}{9}(x^3+1)^{\frac{3}{2}}+C2$

$\frac{7}{3} x^3-2x^2+5x+C$

$\frac{1}{4} x^4 (ln x-\frac{1}{4})+C$

$\frac{1}{3} tan^3 x+C$

$\frac{1}{2} ln|1+e^{2x} |+C$

$\int \frac{7x^3-4x^2+5x}{x}\ dx=$<
$\int x^2\sqrt{x^3+1}\ dx =$
$\int x^2 sen x^3 dx =$
$\int tan^2 x\ sec^2 x\ dx =$
$\int \frac{e^{2x}}{1+e^{2x}}\ dx =$
$\int x^3\ ln x\ dx =$

Al aplicar el método de integración correspondiente se obtienen las integrales especificadas.

Aplicación de la integración

Problema 1. Toma en cuenta la región acotada por la función $f(x)=\frac{x}{1+x^2}$, el Eje $x$, las rectas $x=1$ y $x=3$. Calcula su área.

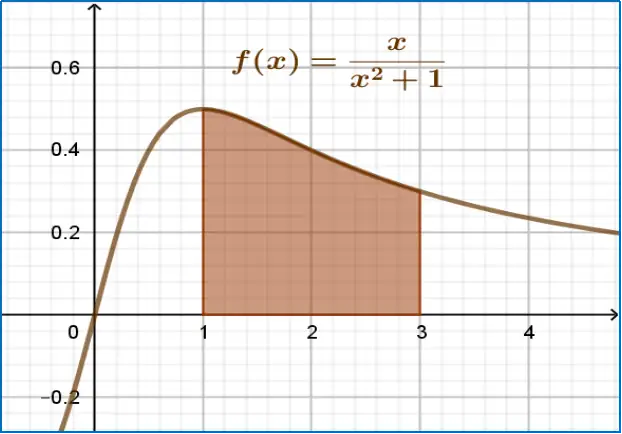
El área de la región sombreada que calculaste escríbela en la siguiente línea en blanco considerando tres lugares para la parte decimal.

Problema 2. Toma en cuenta la región acotada por la función $f(x)=\frac{x}{1+x^2}$, el Eje $x$, las rectas $x=1$ y $x=3$. Calcula su área.

El área de la región sombreada que calculaste escríbela en la línea en blanco considerando tres lugares para la parte decimal.

Problema 3. Se necesita una fuerza de 9 newtons (9 N) para alargar un resorte 2 metros más allá de su posición natural. ¿Cuánto trabajo se necesita para estirar el resorte 5 metros de su posición natural?

Representación gráfica y algebraica del trabajo $W=\int_{a}^{b}F(x) dx$.

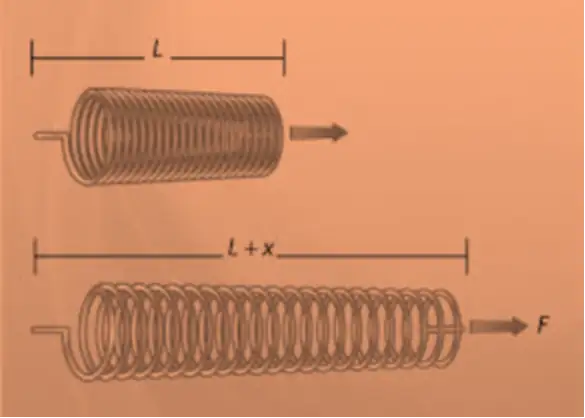
En concordancia con la ley de Hooke el alargamiento o compresión de un resorte cumple con la proporcionalidad entre la fuerza requerida y el alargamiento o compresión del resorte, la cual se representa con la expresión $F(x) = kx$, donde $F(x)$ es la fuerza en newtons necesaria para alargar el resorte $x$ metros de su longitud natural y $k$ es la constante de proporcionalidad. En este contexto el trabajo se define como $W=\int_{a}^{b}F(x) dx$.

Indicaciones para resolver el problema:

Determina la constante de proporcionalidad $k$.
Representa la función fuerza $F(x) = kx$ considerando la $k$ calculada.
Utiliza la expresión $W=\int_{a}^{b}F(x) dx$ para obtener el trabajo.

Desarrolla las indicaciones especificadas para resolver el problema; el trabajo obtenido escríbelo en la línea en blanco considerando la parte entera y dos decimales.

Problema 4. Para $x \geq 20$ el costo marginal en dólares de producir $x$ ceniceros es $C'(x)=\frac{100x}{x^2+1}$. Calcula el costo total en dólares al aumentar la producción de 40 a 50 ceniceros.

Observación, considera que el costo marginal es la razón de cambio en el costo al aumentar la producción de 40 a 50 ceniceros.

Obteniendo la función velocidad.

Datos:

Aceleración de la gravedad ${\color{Green} g=-32\ \frac{pies}{s^{2}}}$

Condiciones iniciales del problema:

En ${\color{Green} t=0}$, ${\color{Green} v(0)=-192\ \frac{pies}{s}}$, ${\color{Green} s(0)=346\ pies}$.

Solución general de la función velocidad ${\color{Green} v(t)=\int -32 dt=-32t+C}$.

Condición inicial en ${\color{Green} t=0}$, ${\color{Green} v(0)=-32(0)+C=-192}$, ${\color{Green} C=-192}$.

Solución particular de la función velocidad es ${\color{Green} v(t)=-32t-192}$.
Determinado la función de posición.

${\color{Green} s(t)=\int v(t)dt}$

${\color{Green} s(t)=\int (-32t-192)dt=-16t^2-192t+C}$, por lo que la solución general de la función posición es ${\color{Green} s(t)=-16t^2-192t+C}$.

Para obtener la solución particular de la función posición se considera la condición inicial, es decir, para ${\color{Green} t=0}$, ${\color{Green} s(0)=346\ pies}$ y al sustituirla en la solución general se obtiene:

${\color{Green} s(0)=-16(0)^2-192(0)+C=346}$, resultando ${\color{Green} C=346}$.

En consecuencia, la función posición es ${\color{Green} s(t)=-16t^2-192t+346}$.
Calculando el tiempo que utilizó el paracaidista al llegar al suelo.

Resolver la ecuación ${\color{Green} s(t)=-16t^2-192t+346=0}$

${\color{Green} t=\frac{-b\pm \sqrt{b^2-4ac}}{2a} = \frac{192\pm \sqrt{(-192)^{2}-4(-16)(346)}}{2(-16)} = \frac{192\pm \sqrt{59008}}{-32}}$

se obtienen los tiempos ${\color{Green} t_1=\frac{192+242.912}{-32}=-13.591}$ s y ${\color{Green} t_2=\frac{192-242.912}{-32}=1.5}$s, se considera el tiempo positivo ya que el negativo no tiene sentido en el contexto del problema.
Obteniendo la velocidad del paracaidista al llegar al suelo.

La velocidad se determina al sustituir el tiempo ${\color{Green} t=1.5}$ en la función velocidad, resultando:

${\color{Green} v(t)=-32t-192}$

${\color{Green} v(1.5)=-32(1.5)-192=-240\ \frac{pies}{s}}$
Obteniendo la velocidad del paracaidista al segundo de haber iniciado el descenso.

De igual forma se sustituye ${\color{Green} t=1}$s en la función velocidad, resultando:

${\color{Green} v(1)=-32(1)-192=-224\ \frac{pies}{s}}$

Integral	Procedimientos
${\color{Green} \int_{1}^{3}\frac{x}{x^2+1}\ dx}$	Integración por cambio de variable.
${\color{Green} u=x^2+1}$, ${\color{Green} du=2x dx}$	Cambio de la variable $x$ por $u$.
${\color{Green} \int_{1}^{3}\frac{x}{x^2+1}\ dx=\frac{1}{2} \int_{1}^{3}\frac{2x\ dx}{x^2+1}}$	Adecuación a integral inmediata $u$.
${\color{Green} =\frac{1}{2} \int_{1}^{3}\frac{2xdx}{x^2+1} = \frac{1}{2}\int_{1}^{3}\frac{du}{u}}$	Integral directa en términos de.
${\color{Green} = \frac{1}{2}\int_{1}^{3}\frac{du}{u} = \frac{1}{2}ln\left \| u \right \|_{1}^{3}}$	Obtención de la integral en términos de $u$.
$\frac{1}{2}ln\left \| u \right \|_{1}^{3}$	Reescribiendo la integral en términos de $x$.
$\frac{1}{2}ln\left \| x^{2}+1 \right \|_{1}^{3}=\frac{1}{2}\left ( ln 10 - ln 2 \right )=0.804$	Área de la región.

Integral indefinida y definida	Procedimientos
${\color{Green} \int 3xe^{-\frac{x}{3}} dx}$	Integración por partes.
${\color{Green} u=3x}$, ${\color{Green} du=3dx}$ ${\color{Green} dv=e^{-\frac{x}{3}} dx}$, ${\color{Green} v=\int e^{-\frac{x}{3}} dx=-3e^{-\frac{x}{3}}}$	Elección de la función $u$ y la diferencial $dv$.
${\color{Green} \int 3xe^{-\frac{x}{3}} dx = -9xe^{-\frac{x}{3}}-\int -3e^{-\frac{x}{3}} (3 dx)}$	Aplicando la integración por partes.
${\color{Green} \int 3xe^{-\frac{x}{3}} dx = -9xe^{-\frac{x}{3}}+9\int e^{-\frac{x}{3}} dx =}$	Reagrupando la integral.
${\color{Green} = -9xe^{-\frac{x}{3}}+9\int e^{-\frac{x}{3}} dx =-9xe^{-\frac{x}{3}} - 27e^{-\frac{x}{3}}+C}$	Antiderivada obtenida.
${\color{Green} \int_{0}^{9}3xe^{-\frac{x}{3}} dx= \left [ -9xe^{-\frac{x}{3}} - 27e^{-\frac{x}{3}}+C\right ]_{0}^{9} }$	Integral definida.
${\color{Green} [-9(9)e^{-3} -27e^{-3}+C]-[-9(0) e^0-27e^0+C]=[-5.3770]-[-27]=21.623}$	Área de la región.

Expresión matemática	Procedimientos
${\color{Green} F(x) = kx}$	Función fuerza.
${\color{Green} F(2) = 2k=9}$	Sustitución de datos en la función fuerza.
${\color{Green} 2k=9}$, ${\color{Green} k=\frac{9}{2}}$	Cálculo de la constante de integración.
${\color{Green} F(x) = \frac{9}{2} x}$	Obtención de la función fuerza.
${\color{Green} W=\int_{0}^{5}\frac{9}{2} x\ dx=\frac{9}{2}\int_{0}^{5}x dx}$	Reescribiendo la integral.
${\color{Green} W=\frac{9}{2}\int_{0}^{5}x dx =\frac{9}{4}\left [ x^2 \right ]_{0}^{5}=\frac{9}{4}\left ( 25-0 \right )=\frac{225}{4}=56.25\ Joules.}$	El trabajo solicitado.

Expresión matemática	Procedimientos
${\color{Green} C(x)=\int_{40}^{50}\frac{100x}{x^2+1}\ dx }$	Función costo marginal.
${\color{Green} C(x)=\int_{40}^{50}\frac{100x}{x^2+1} dx = 100\int_{40}^{50}\frac{x dx}{x^2+1}}$	Reescribiendo la integral.
${\color{Green} u=x^2+1}$, ${\color{Green} du=2x\ dx}$	Integración por cambio de variable.
${\color{Green} 100\int_{40}^{50}\frac{x\ dx}{x^2+1}=100\left ( \frac{1}{2} \right ) \int_{40}^{50}\frac{x\ dx}{x^2+1}}$	Transformación a una integral inmediata.
${\color{Green} 50\int_{40}^{50}\frac{du}{u}=50\left [ ln u \right ]_{40}^{50}}$	Integral en términos de $u$.
${\color{Green} 50\left [ ln (x^2+1) \right ]_{40}^{50}}$	Escribiendo la integral en términos de $x$.
${\color{Green} 50\left [ln\left ( x^2+1 \right ) \right ]_{40}^{50}=50(ln 2501-ln 1601)=22.3}$	Costo marginal en dólares en la producción de 10 ceniceros adicionales.

Actividad final

Problemas que involucran condición inicial

Aplicación de los métodos de integración

Aplicación de la integración

Síguenos

Sitios de interés

Nosotros

Escolares

Newsletter