El estudio del Cálculo Diferencial está relacionado con la obtención de la derivada de funciones, su interpretación geométrica como la pendiente de la recta tangente a la gráfica de una función en el punto de tangencia, y su aplicación en la resolución de problemas de optimización en diversos contextos. El siguiente problema ilustra una de sus aplicaciones, así como, su relación con el cálculo integral.
Problema (caída libre)
Un clavadista salta desde una plataforma de 30 pies, su velocidad inicial es de 5 pies por segundo (hacia arriba), ¿en qué tiempo hará contacto con el agua?, ¿cuál será su velocidad y aceleración al momento del impacto?; recordemos que para la resolución del problema se utiliza la función de posición de un objeto en caída libre. Dicha función supone que la resistencia del aire es insignificante y está dada por $s(t)=s_0+v_0 t+\frac{1}{2} gt^2$, donde $s(t)$ es la posición (altura) del clavadista en pies, $t$ es el tiempo en segundos, $g=-32\ \frac{pies}{^{seg^{2}}}$ es la aceleración de la gravedad, $v_0$ es la velocidad inicial, y $s_0$ es la altura inicial. Sustituyendo $s_{0}=30\ pies$, $v_0=5 pies/seg$ y la aceleración de la gravedad $g$ en la función de posición se obtiene $s(t)=30+5t-16t^2$. La gráfica distancia versus tiempo se representa en la siguiente figura.
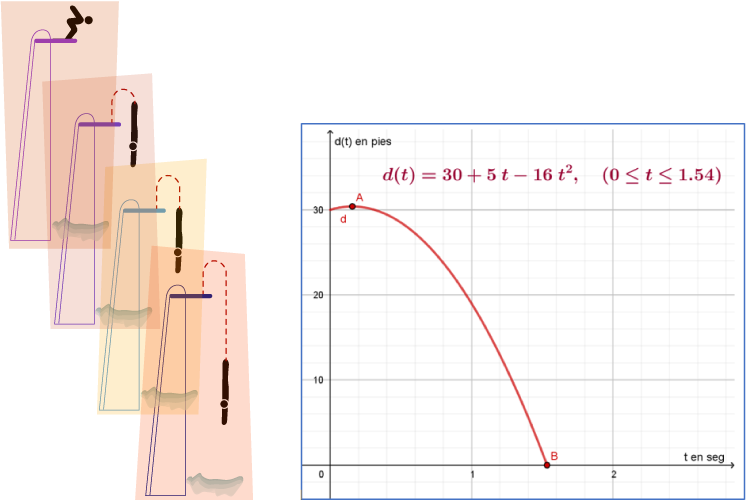
Para la resolución del problema primero debe determinarse el tiempo en el que el clavadista hace contacto con el agua y después se sustituye en la función velocidad (derivada de la función posición) y en la aceleración (derivada de la función velocidad).
El tiempo que utiliza el clavadista para impactarse con el agua se obtiene al resolver la ecuación $s(t)=0$, es decir, $-16t^2+5t+30=0$, en la solución de la ecuación se utiliza la fórmula general de segundo grado considerando $a=-16$, $b=5$ y $c=30$ como se muestra a continuación:
$t=\frac{-b\pm \sqrt{b^{^{2}}-4a+c}}{2a}=\frac{-5\pm \sqrt{(5)^{2}-4(-16)(30)}}{2(-16)}=\frac{-5\pm \sqrt{1945}}{-32}=\frac{-5\pm 44.10}{-32}$, por lo que las soluciones son $t_1=-1.22$ y $t_2=1.53$ segundos, como el tiempo negativo no tiene sentido en el contexto del problema se considera el tiempo positivo.
Recordemos que la velocidad instantánea es la derivada de la función posición, por lo que resulta $v(t)=s'(t)=5-32t$, al sustituir en ésta el tiempo $t_2=1.53$ segundos, se determina la velocidad instantánea del clavadista al hacer contacto con el agua, por lo que su valor $v(1.53)=5-32(1.53)=-43.96\ \frac{pies}{s}$.
Finalmente, para obtener la aceleración del clavadista al impactarse con el agua, se deriva la función velocidad y se sustituye en ésta el tiempo de impacto, es decir, la aceleración es $g(t)=v'(t)=-32\ \frac{pies}{s^{2}}$, por lo que la aceleración del clavadista al hacer contacto con el agua es $g(1.53)=v'(1.53)=-32\ \frac{pies}{s^{2}}$.
Ahora consideremos el problema inverso con los datos especificados, es decir, dada la aceleración de la gravedad, determinemos las funciones velocidad y posición del clavadista, para ello, partimos de la aceleración de la gravedad $g(t)=-32\ \frac{pies}{s^{2}}$ y determinemos la velocidad considerando la condición inicial $v_0=5\ \frac{pies}{s}$ en el tiempo $t=0\ s$, para ello, busquemos una función cuya derivada sea $g(t)=-32$, con base en los aprendizajes que lograste para el cálculo de derivadas estarás de acuerdo que la función $v(t)=-32t$ cumple puesto que $v'(t)=g(t)=-32$, sin embargo, las funciones $v(t)=-32t+1$ y $v(t)=-32t-9$ también cumplen, ya que la derivada de una función constante es cero, en consecuencia la función $v(t)=-32t+C$, para cualquier constante $C$ es una familia de funciones que cumplen con lo especificado y se le llama la solución general que difieren en una constante $C$, además, debe satisfacer que en el tiempo $t=0\ s$ su velocidad es $v_0=5\ \frac{pies}{s}$ que al sustituirla en la solución general de la velocidad $v(0)=-32(0)+C=5$, resulta $C=5$ y al reemplazarla en la solución general se obtiene una solución particular $v(t)=-32t+5$; ahora obtengamos la función posición cuya derivada sea $v(t)=-32t+5$, de igual forma estarás de acuerdo que la función $s(t)=-16t^2+5t$ satisface que su derivada es la función velocidad, es decir, $'(t)=v(t)=-32t+5$, sin embargo, no es única ya que las funciones $s(t)=-16t^2+5t-3$ y $'(t)=v(t)=-32t+5$ también cumplen, luego entonces la función buscada resulta ser la familia de funciones $s(t)=-16t^2+5t+C$ (solución general) que difieren en un constante $C$ y debe satisfacer que en el tiempo $t=0\ s$, la función posición $s(0)=-16(0)^2+5(0)+C=30$ por lo que la solución particular es la función posición $s(t)=-16t^2+5t+30$ dada al inicio del problema.
El siguiente esquema ilustra la solución de ambos problemas

De los procedimientos realizados en la solución del problema y del esquema se observa que la operación inversa de la derivación es la integración de funciones cuya solución involucra a una familia de funciones en la que la función $F(x)$ es una antiderivada de la función $f(x)$, es decir, $F'(x)=f(x)$, en consecuencia todas las antiderivadas de $f(x)$ es la familia de funciones de la forma $F(x)+C$, donde C es la contante de integración, para la obtención de la familia mencionada en el presente material se estudiará la integración inmediata de funciones, métodos de integración y su aplicación a la resolución de problemas.
Con este material establecerás mediante el análisis de situaciones de variación, la integral indefinida (antiderivadas) de diversas funciones y utilizarás fórmulas inmediatas y algunos métodos de integración, para obtener la integral de funciones, así como, su aplicación a la resolución de problemas en diversos contextos.


