En concordancia con los ejemplos presentados para la búsqueda de la antiderivada (integral indefinida) de una función, se requieren de los aprendizajes que lograron los estudiantes sobre la obtención de las derivadas de las funciones algebraicas y trascendentes, los cuales, incidirán en la adquisición de las habilidades y destrezas en la formulación de algunas reglas inmediatas de integración y su aplicación en la integración de funciones.
Integración de la función constante $f(x)=k$
Consideremos la función constante $f(x)=5$ y determinemos su integral indefinida, para ello, obtengamos una función $F(x)$, tal que $F'(x)=f(x)$. Con base en el aprendizaje que lograste sobre la obtención de la derivada de funciones constantes estarás de acuerdo que la función $F(x)=5x$ cumple, puesto que su derivada es $F'(x)=5$, es decir, $F'(x)=f(x)$, sin embargo, las funciones $F(x)=5x+1$, $F(x)=5x-7$ y $F(x)=5x+C$, donde $C$ es un número constante también cumplen ya que su derivada es la constante $5$, luego entonces la integral indefinida es una familia de funciones que difieren en una constante.

Revisa e interactua el siguiente recurso GeoGebra Integral de la función constante.
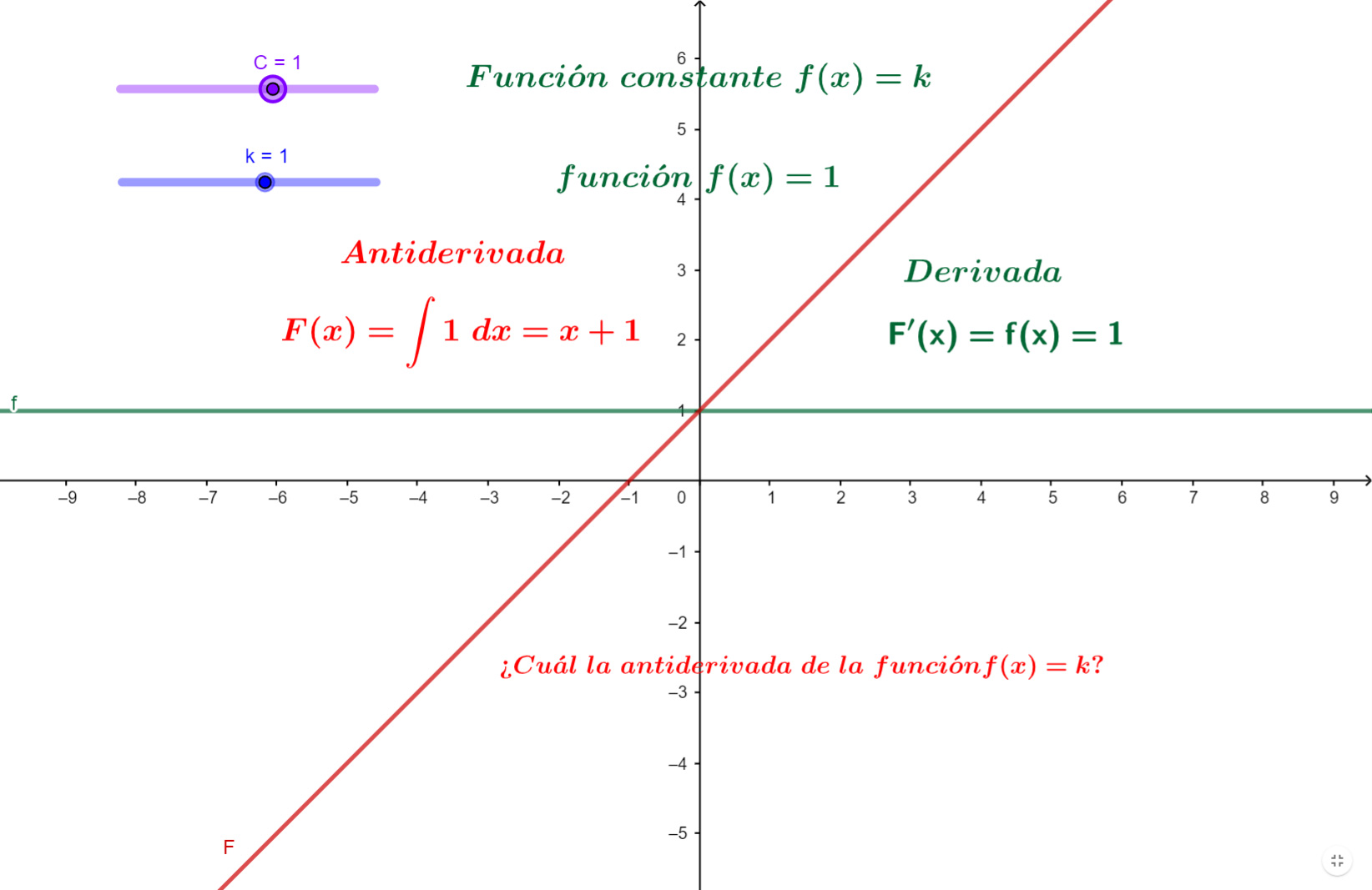
Con base en tu interacción con el recurso GeoGebra para valores particulares de $k$ y $C$, observaste que la antiderivada se obtuvo con el producto de la constante $k$ y la variable $x$ $\int 7 dx=7x$, además, al arrastrar la constante $C$ se obtuvieron otras antiderivadas particulares, por ejemplo, $F(x)=7x-8$, $F(x)=7x+5$, entre otras. Ahora con base en la regularidad de las antiderivadas, elige la antiderivada general de la función constante $f(x)=k$.
Para que avances en la comprensión y aplicación, aplica la integral indefinida de la función constante (Regla 1) y determina las integrales indefinidas especificadas en el siguiente ejercicio.
Integración de funciones constantes
Con este ejercicio, obtendrás la integral indefinida (antiderivadas) de las funciones constantes que se indican utilizando la regla 1.
Arrastra las opciones que se presentan según corresponda. Las respuestas correctas aparecerán en color verde.
| $\int 1 dx=$ | |
| $\int 5dx=$ | |
| $\int\frac{1}{2} dx=$ | |
| $\int -5dx=$ | |
| $\int -\frac{4}{5} dx=$ |
Al aplicar la regla para la integral de la función constante $\int k dx = kx + C$, se obtienen las integrales solicitadas.
- $\int 1 dx= x+C$
- $\int 5dx= 5x+C$
- $\int\frac{1}{2} dx=\frac{1}{2}x+C$
- $\int -5dx=-5x+C$
- $\int -\frac{4}{5} dx=-\frac{4}{5}x+C$


