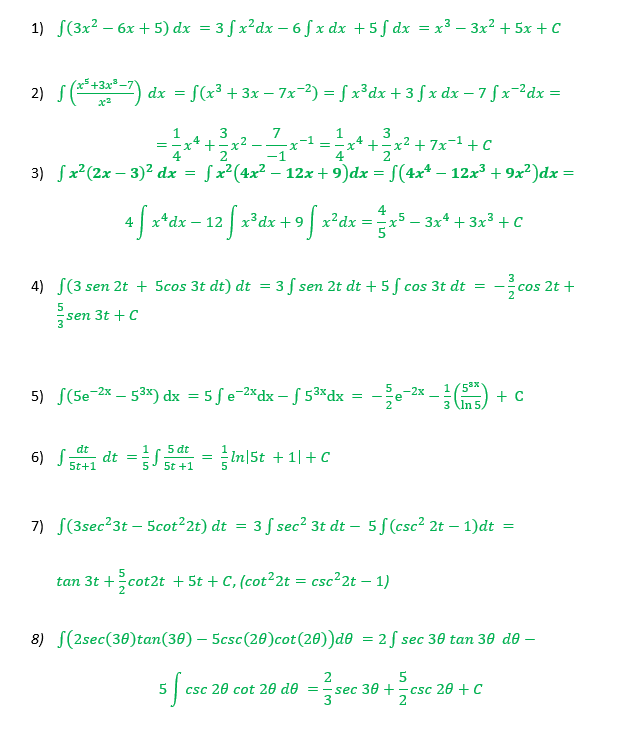En este apartado obtendrás las reglas para la integración de las funciones trigonométricas $f(x)=A sen(Bx)$, $g(x)=A cos(Bx)$, $h(x)=A tan(x)$, $f(x)=A cot(Bx)$, $g(x)=A sec^{2} (Bx)$ y $g(x)=A csc^{2} (Bx)$, mediante tu interacción con el recurso GeoGebra, para la formulación de reglas para la integración de las funciones mencionadas.

Revisa e interactua el siguiente recurso GeoGebra Integral de funciones trigonométricas.
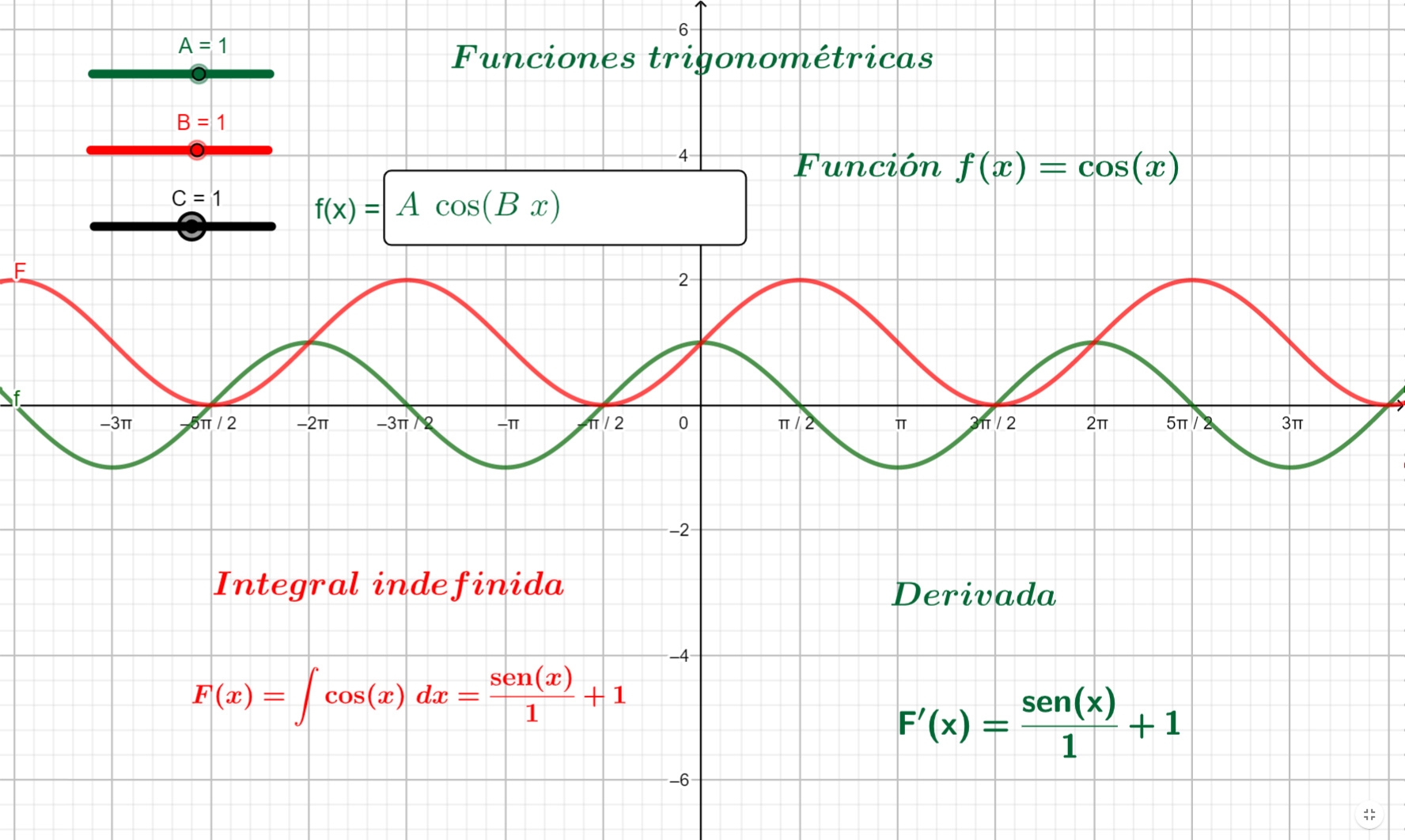
Con base en la interacción que realizaste con el recurso GeoGebra, elige la integral de las funciones que se indican en el ejercicio siguiente.
Integración de funciones trigonométricas 1
Con este ejercicio, obtendrás la integral de las funciones trigonométricas que se indican, mediante la regularidad de integrales para casos particulares de las funciones mencionadas, para la formulación de las reglas de integración para las funciones mencionadas.
Indica cuál es la integral de las funciones trigonométricas que se presentan arrastrando las opciones al lugar que le corresponde. Las respuestas correctas aparecerán en color verde.
| $\int A sen(Bx) dx =$ | |
| $\int A cos(Bx) dx =$ | |
| $\int A tan(Bx)dx =$ | |
| $\int A cot(Bx) dx =$ | |
| $\int A sec^2 (Bx) dx=$ | |
| $\int A csc^2 (Bx) dx=$ |
Los procedimientos utilizados en la resolución del problema se presentan a continuación
Integración de funciones trigonométricas 2
Con este ejercicio, obtendrás la integral de las funciones trigonométricas que se indican utilizando la regla para la integral de las funciones mencionadas.
Indica cuál es la integral de las funciones trigonométricas que se presentan arrastrando las opciones al lugar que le corresponde. Las respuestas correctas aparecerán en color verde.
| $\int 5cos(2x)dx=$ | |
| $\int -5sen(-3x)dx=$ | |
| $\int 7sec^2 (x)dx=$ | |
| $\int -4csc^2 (x)dx=$ | |
| $\int 3tan(5x)dx=$ | |
| $\int -2cot(3x)dx=$ |
Los procedimientos utilizados en la resolución del problema se presentan a continuación
La obtención de integrales de funciones algebraicas y trigonométricas se realizó mediante ensayos relacionados con las reglas de derivación, sin embargo, para facilitar el cálculo de integrales se utilizan tablas de integrales inmediatas; para determinar una integral cualquiera la identificamos en la tabla, si ésta existe se obtiene la integral como se indica en la tabla, en caso contrario, se realizarán las transformaciones algebraicas pertinentes para convertirla en una integral inmediata. Las integrales inmediatas se presentan en la tabla.
| Fórmulas de diferenciación | Fórmulas de integración básicas | Fórmulas de integración generales |
|---|---|---|
| $\frac{d}{dx} x = 1$ | $\int dx = x + C$ | $\int du = u + C$ |
| $\frac{d}{dx}\frac{x^{n+1}}{n+1} = x^n,n\neq -1 $ | $\int x^n dx = \frac{x^{n+1}}{n+1}+C$ | $\int u^n du = \frac{u^{n+1}}{n+1}+C$ |
| $\frac{d}{dx}a^x=a^x\ lna$ | $\int a^x dx= \frac{a^{x}}{ln a}+C$ | $\int a^u du= \frac{a^{u}}{ln a}+C$ |
| $\frac{d}{dx}ln |x| = 1/x$ | $\int \frac{1}{x} dx= ln |x|+ C$ | $\int \frac{1}{u} du= ln |u|+ C$ |
| $\frac{d}{dx}sen x = cos x$ | $\int cos x dx = sen x + C$ | $\int cos u du = sen u + C$ |
| $\frac{d}{dx}cos x = -sen x$ | $\int sen x dx = -cos x + C$ | $\int sen u du = -cos u + C$ |
| $\frac{d}{dx}tan x = sec^2 x$ | $\int sec^2 x\ dx = tan x + C$ | $\int sec^2 u\ du = tan u + C$ |
| $\frac{d}{dx}cot x = -csc^2 x$ | $\int csc^2 x dx = -cot x + C$ | $\int csc^2 u du = -cot u + C$ |
| $\frac{d}{dx}sec\ x = sec\ x\ tan\ x$ | $\int sec\ x\ tan x\ dx = sec\ x +C$ | $\int sec\ u\ tan u\ du = sec\ u +C$ |
| $\frac{d}{dx}csc\ x = -csc\ x\ cot\ x$ | $\int csc\ x\ cot\ x\ dx = -csc\ x +C$ | $\int csc\ u\ cot\ u\ du = -csc\ u +C$ |
Los siguientes ejemplos muestran la aplicación de las reglas de integración para la obtención de integrales de funciones:
$\int 3x^2-5x-7)dx=3\int x^2 dx-5\int x dx-7\int dx=x^3-\frac{5}{2} x^2-7x+C$
$\int \frac{(x+1)(x-2)}{\sqrt{x}}=\int \left ( \frac{x^2-x-2}{x^{\frac{1}{2}}} \right )dx=\int \left ( x^{\frac{3}{2}} -x^{\frac{1}{2}}-2x^{-\frac{1}{2}}\right )dx$
$$=\frac{x^{\frac{5}{2}}}{\frac{5}{2}}-\frac{x^{\frac{3}{2}}}{\frac{3}{2}}-\frac{2x^{\frac{1}{2}}}{\frac{1}{2}}+C =\frac{2}{5}x^{\frac{5}{2}}-\frac{2}{3}x^{\frac{3}{2}}-4x^{\frac{1}{2}}+C$$
$\int \frac{x^3-6x+5}{x}dx=\int (x^2-6+\frac{5}{x})dx=$
$$\int x^2 dx- 6\int dx+5\int \frac{dx}{x}=\frac{x^{3}}{3}-6x+5ln(x)+C$$
$\int sen 3x\ dx =-\frac{cos 3x}{3}+ C$
$\int Sec^2 2\theta\ d\theta = \frac{tan 2\theta }{2}+C$
$\int tan^2 x\ dx=\int \left (sec^2 x-1 \right )dx = \int sec^2 x\ dx-\int dx= tan(x)-x+C$ ($tan^2 x=sec^2x-1$)
$\int (3+e^{5x} )dx=3\int dx +\int e^{5x} dx = 3x +\frac{e^{5x}}{5}+C$
Integración de funciones trigonométricas 3
Con este ejercicio, determinarás la integral de las funciones algebraicas y trascendentes que se indican utilizando la integración inmediata.
Arrastra las siguientes integrales al lugar que corresponde en la tabla. Las respuestas correctas aparecerán en color verde.
| $\int (3x^2-6x+5) dx =$ | |
| $\int \left (\frac{x^5+3x^3-7}{x^2} \right ) dx =$ | |
| $\int x^2 (2x-3)^2 dx = $ | |
| $\int (3 sen 2t + 5cos 3t) dt = $ | |
| $\int (5e^{-2x}-5^{3x}) dx =$ | |
| $\int \frac{dt}{5t+1}=$ | |
| $\int \left ( 3sec^2 3t-5csc^2 2t \right ) dt = $ | |
| $\int (2sec 3\theta\ tan3\theta -5csc2\theta\ cot2\theta ) d\theta = $ |
Los procedimientos utilizados en la resolución del problema se presentan a continuación