Demostración del Teorema de Pitágoras

En el aprendizaje de la Geometría es importante dar una justificación o demostración de los resultados que se obtienen (Teoremas) y no solo querer saber recetas o fórmulas. En este apartado veremos cuatro diferentes demostraciones del Teorema de Pitágoras, las cuales consisten en una serie de pasos (Afirmaciones) con su justificación (Razones). Algunas de estas demostraciones son más intuitivas que otras, pero todas contribuyen en diversos grados a nuestro desarrollo intelectual y el conocimiento de la Geometría.

En algunos pasos y justificaciones se require que completes las partes faltantes de la argumentación que se da en la demostraciones -enmarcadas en color gris- para que comprendas mejor el desarrolo de la Geometría y su aplicación.

Teorema de Pitágoras:

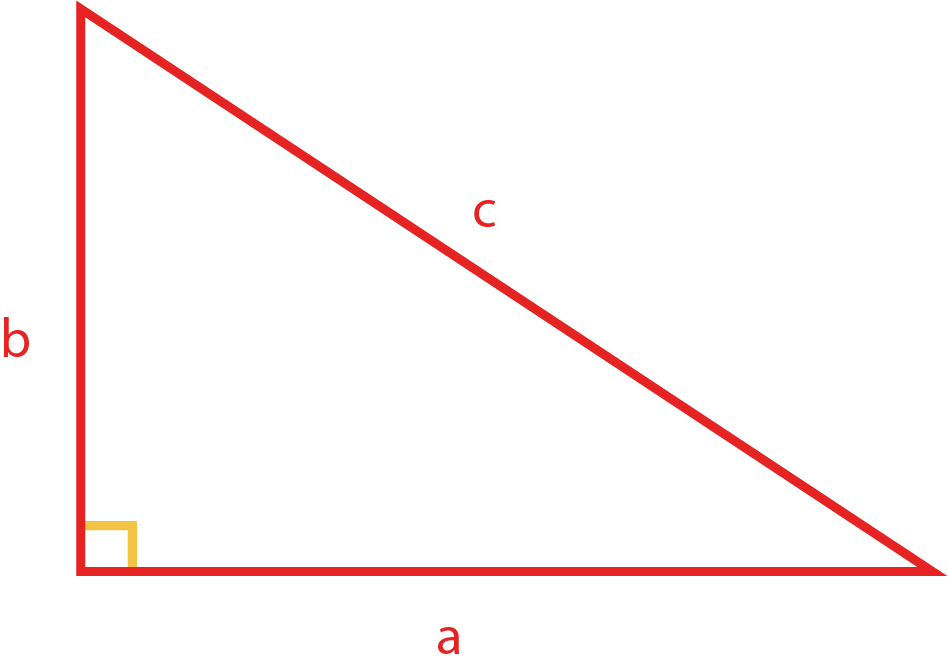
En un triángulo rectángulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.

Hipótesis: Sea un Triángulo rectángulo de catetos a y b,con hipotenusa c

Tesis: $a^2+b^2=c^2$

Triángulo rectángulo
Geogebra

En el recurso Geogebra se muestra una figura, donde se tiene un cuadrado de lado $c$ y cuatro triángulos rectángulos congruentes con catetos $a$, $b$ y con hipotenusa $c$. Este recurso te ayudará a comprender la demostración del Teorema de Pitágoras siguiendo las instrucciones que se dan y explorándolo libremente las veces que consideres necesario. Después completa la información de la tabla.

Demostración

Afirmaciones Razones

1. El área del cuadrado $A_C$ de lado $c$ es

$A_C=c^2$

El área de un cuadrado es lado por

2. El área de cada triángulo $A_R$ es

$A_R=$
$ab$

El área de un triángulo es base por altura entre 2 , que en los triángulos rectángulos un cateto es la base y el otro cateto la

3. El área del cuadrado chico $A_{CP}$ de lado $(a-b)$ es

$A_{CP}=(a-$ $)^2$

El área de un cuadrado es lado por lado

4. El área del cuadrado de lado $c$ es igual a $A_C=4A_R+A_{CP}$

El cuadrado se compone de los cuatro triángulos congruentes y el cuadrado pequeño
5. $c^2=4\left( \tfrac{ab}{2} \right)+(a-b)^2$

Sustituyendo los valores de

$A_C=c^2$, $A_R=\tfrac{ab}{2}$ y $A_{CP}=(a-b)^2$
6. $c^2=2ab+(a-b)^2$

Simplificando $4( \tfrac{ab}{2})=$ $ab$
7. $c^2=2ab+a^2-2ab+b^2$ Sustituyendo $(a-b)^2=a^2-2ab+b^2$

8. $c^2=a^2+b^2$

o también $a^2+b^2=c^2$

Simplificando paso 7 obtenemos el Teorema de Pitágoras:

En un triángulo rectángulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.

En un triángulo rectángulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.

Hipótesis: Sea un Triángulo rectángulo de catetos a y b,con hipotenusa c

Tesis: $a^2+b^2=c^2$

Triángulo rectángulo
Geogebra

En el recurso Geogebra se muestran cuadrados de lados $a+b$, de lado $a$ , de lado $b$ y de lado $c$, además de triángulos rectángulos congruentes con catetos $a$, $b$ y con hipotenusa $c$. Este recurso te ayudará a comprender la demostración del Teorema de Pitágoras. Al terminar completa la información de la tabla.

Demostración

Afirmaciones Razones

1. De la figura 1 se tiene que:

El área del cuadrado grande $A_{C1}$ de lado $a+b$ es igual a

$A_{C1}=4A_T+A_1+A_2$

Porque el cuadrado grande $A_{C1}$ de lado $a+b$ se compone de los cuatro triángulos congruentes de área $A_T$, el cuadrado de área $A_1$ y el cuadrado de área $A_2$

2. De la figura 2 se tiene que:

El área del cuadrado grande $A_{C2}$ de lado $a+b$ es igual a:

$A_{C2}=$ $A_T+A_3$

Porque el cuadrado grande $A_{C2}$ de lado $a+b$ se compone de los cuatro triángulos congruentes de área $A_T$ y el cuadrado de área $A_3$

3. $A_T+A_1+A_2=$ $A_T+A_3$

De 1, 2 y $A_{C2}=A_{C1}$ porque los dos son cuadrados de lado $a+b$

4. $A_1+A_2=A_3$ Simplificando

5. El área de los cuadrados $A_1$ de lado $a$ es:

$A_1=a^2$

Porque el área de un cuadrado es la medida de su lado al cuadrado

6. El área del cuadrado $A_2$ de lado $b$ es

$A_2=$$^2$

Porque el área de un cuadrado es la medida de su lado al

7. El área del cuadrado $A_3$ de lado es

$A_3=c^2$

Porque el área de un cuadrado es la medida de su al cuadrado

8. $a^2+b^2=c^2$

Sustituyendo 5, 6 y 7 en 4 se obtiene el teorema de Pitágoras:

Simplificando obtenemos el Teorema de Pitágoras:

En un triángulo rectángulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.

Teorema de Pitágoras:

En un triángulo rectángulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.

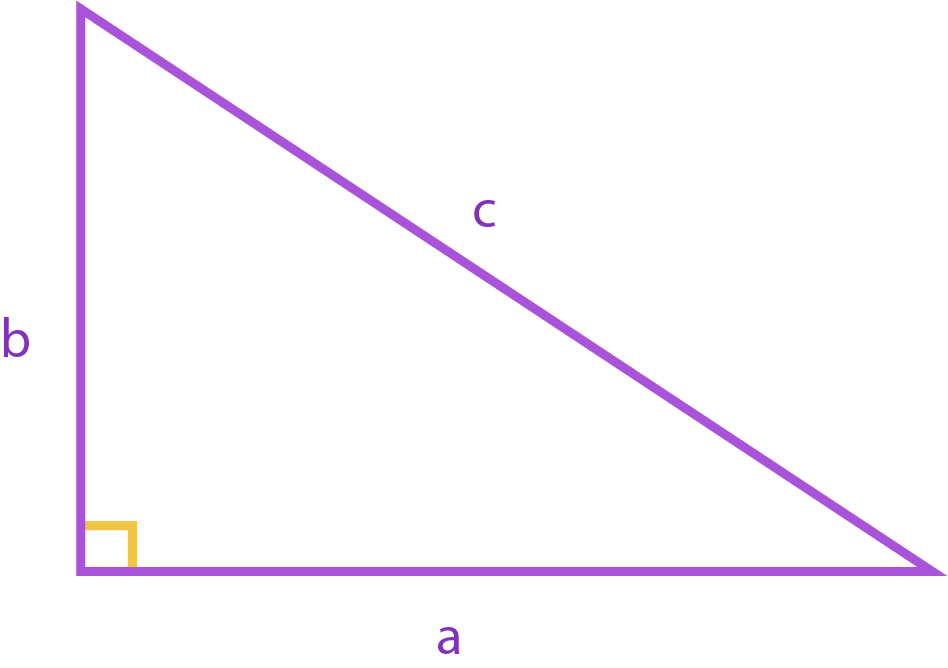
Hipótesis: Sea un Triángulo rectángulo de catetos $a$ y $b$,con hipotenusa $c$

Tesis: $a^2+b^2=c^2$

Triángulo rectángulo

Los triángulos semejantes tienen la misma forma y pueden ser de diferente o igual tamaño.

En esta demostración se utilizan las propiedades de triángulos semejantes:

Dos triángulos son semejantes cuando tienen sus ángulos correspondientes congruentes y las razones entre sus lados correspondientes son iguales.

Geogebra

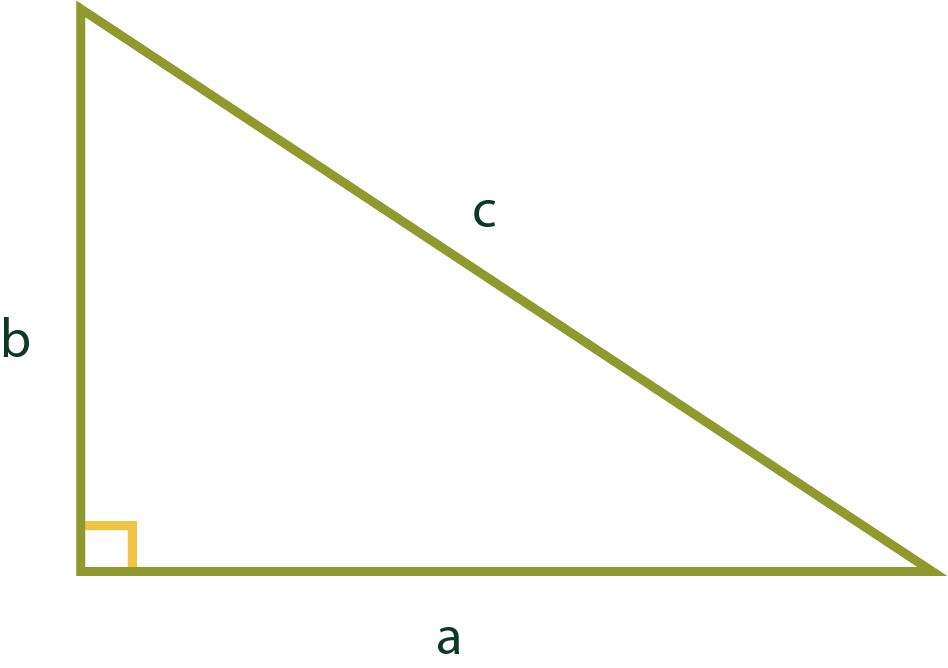
En el recurso Geogebra se tiene un triángulo rectángulo de catetos a ,b y con hipotenusa c. Este triángulo se puede dividir en otros dos triángulos semejantes con él.

Después de revisar el recurso completa los espacios en la tabla y después da clic en Verificar para comprobar tus respuestas.

Demostración

Afirmaciones Razones

1. Los triángulos $T1$ y $T2$ son semejantes

Los ángulos correspondientes son congruentes:

En ángulo recto, el ángulo en común $B$ y el ángulo restante $DAC=BCD$ (Teorema $AAA$: Ángulo-Ángulo-Ángulo)

2. $\tfrac{a}{e}=\tfrac{b}{d}=\tfrac{c}{a}$

Por las propiedades de los triángulos semejantes $T1$ y $T2$

3. De $\tfrac{a}{e}=\tfrac{c}{a}$ se obtiene $a^2=ce$

Multiplicando por ae cada lado de la igualdad $ae \left( \tfrac{a}{e} \right) = \left( \tfrac{c}{a} \right)$ y simplificando se obtiene $a^2=ce$
4. Los triángulos $T1$ y $T3$ son:

Los ángulos correspondientes son congruentes:

En ángulo recto, el ángulo en común A y el ángulo restante DBC=DCA (Teorema AAA: Ángulo-Ángulo-Ángulo)

5. $\tfrac{a}{d}=\tfrac{b}{f}=\tfrac{c}{b}$

Por la semejanza de los triángulos $T1$ y

6. De $\tfrac{b}{f}=\tfrac{c}{b}$ se obtiene $b^2=cf$

Multiplicando por $bf$ cada lado de la igualdad:

$bf \left( \tfrac{b}{f} \right) = \left( \tfrac{c}{b} \right) bf$, y simplificando $b^2=$

7. $a^2+b^2=ce+cf=c(e+f)$

De pasos 3, 6 y factorizando

8. $e+f=$

El lado $c$ del triángulo se dividió en los segmentos $e$ y $f$, de acuerdo con la figura
9. $a^2+b^2=c(c)$ Sustiyuyendo 8 en 7
10. $a^2+b^2=c^2$

Simplificando, se obtiene el Teorema de Pitágoras:

En un triángulo rectángulo la suma de los cuadrados de los es igual al cuadrado de la .

Aquí solo se da la idea general de la demostración, para ver la versión completa en detalle revisa el Para saber más del final.

Teorema de Pitágoras:

En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Hipótesis: Sea un Triángulo rectángulo de catetos $a$ y $b$,con hipotenusa $c$

Tesis: $a^2+b^2=c^2$

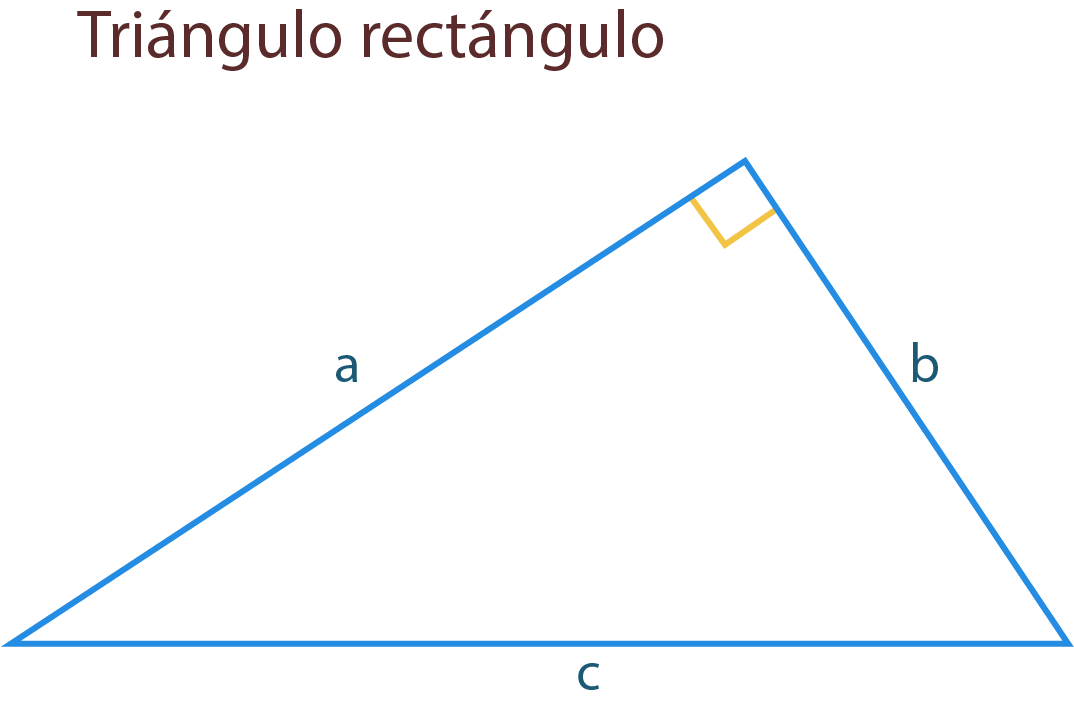
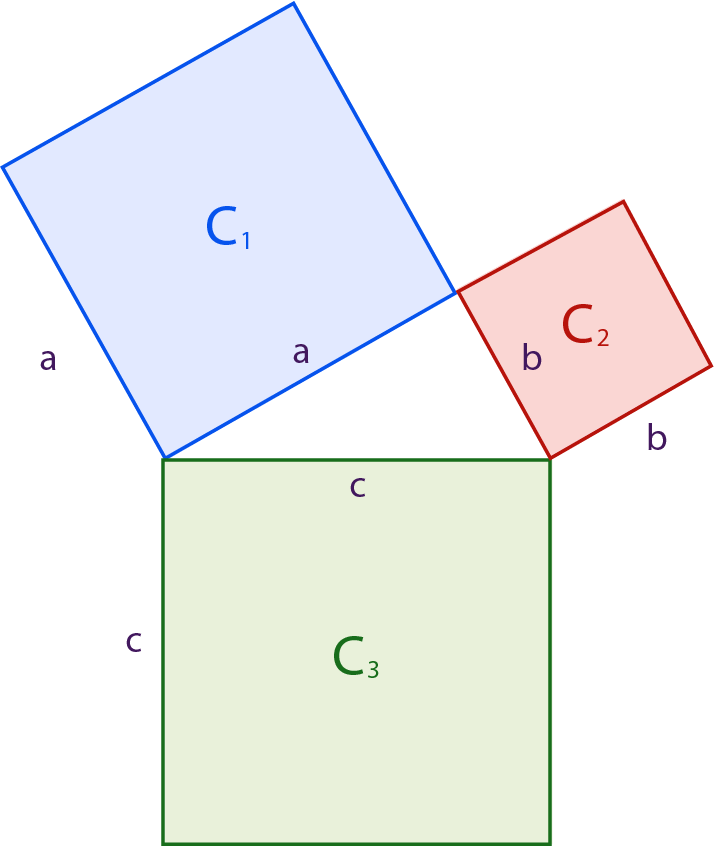
Triángulo rectángulo
Triángulo rectángulo
Triángulo rectángulo

La figura muestra un triángulo rectángulo de catetos $a$, $b$ y de hipotenusa $c$, además de cuadrados construidos sobre éstos.

Área del cuadrado $C_1=a^2$

Área del cuadrado $C_2=b^2$

Área del cuadrado $C_3=c^2$

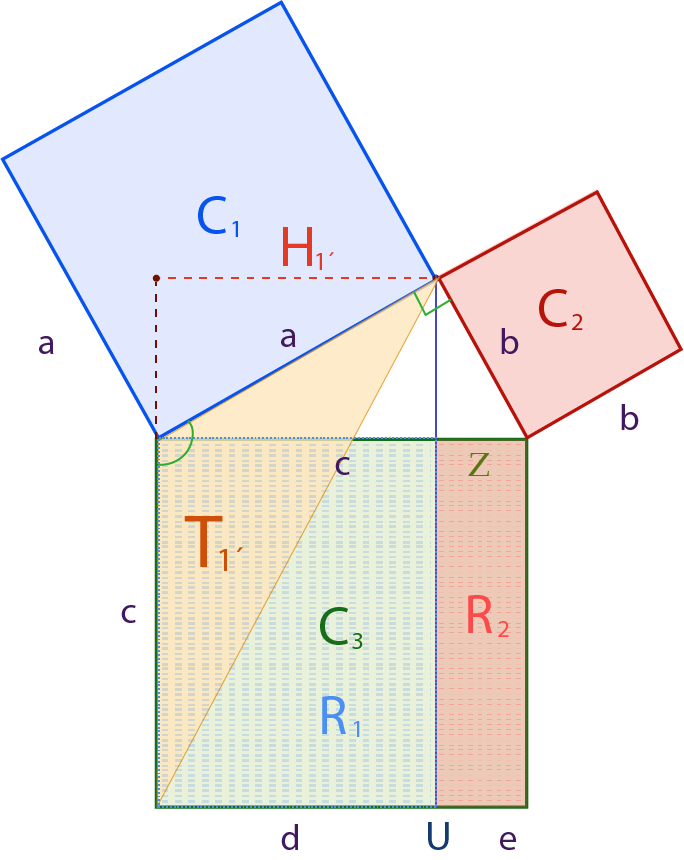
La idea de la demostración es la siguiente:

Sabemos que el área de un triángulo es base por altura entre 2 y cada lado del triángulo es una base que tiene su altura correspondiente, que es la longitud del segmento perpendicular que va de la base o su prolongación al vértice opuesto.

Construyendo ciertos triángulos en la figura se comprueba que:

  1. El área de cuadrado de color azul $C_1=a^2$ sobre el cateto $a$ es igual al área del rectángulo punteado de color azul $R_1=cd=a^2$.
  2. El área de cuadrado de color rojo $C_2=b^2$ sobre el cateto $b$ es igual al área del rectángulo punteado de color rojo $R_2=ce=a^2$.

Como el área del cuadrado sobre la hipotenusa $C_3$ de color verde está formado por los rectángulos $R_1$ y $R_2$ se tiene $R_1+R_2=C_3$.

Sutituyendo $R_1=a^2$, $R_2=b^2$ y $C_3=c^2$ en la igualdad $R_1+R_2=C_3$, se obtiene el Teorema de Pitágoras

$a^2+b^2=c^2 .$

Para saber más. Revisa la demostración 4 completa .