Teorema de Pitágoras: Triángulo rectángulo
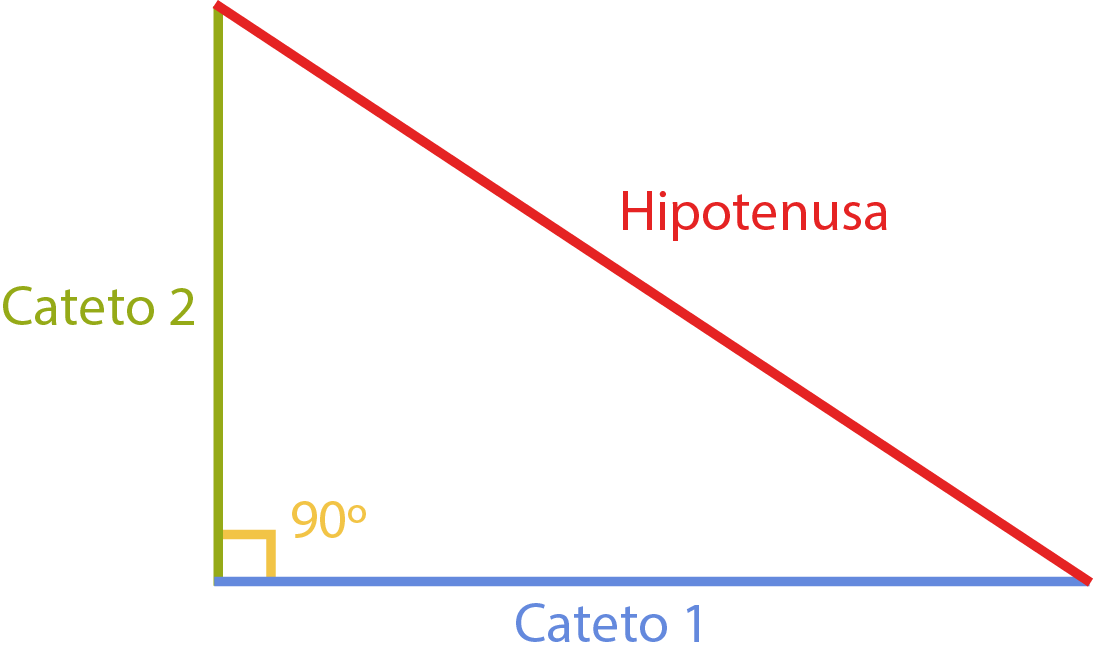
El Teorema de Pitágoras relaciona las longitudes de los tres lados de un triángulo rectángulo. Un triángulo rectángulo es aquel que tiene un ángulo recto (90 grados), como se muestra en la figura:
Los lados que forman el ángulo recto se llaman catetos y el lado opuesto al ángulo recto se llama hipotenusa, es el lado mayor.

A continuación explorarás el recurso Geogebra en el que se ilustran diferentes posibilidades de cuadrados construidos sobre los lados de triángulos de distintos tipos, para establecer las condiciones que se cumplen en el Teorema de Pitágoras.
Después del trabajo con el recurso GeoGebra contesta la siguientes preguntas. Al terminar da clic en Verificar.
De las observaciones del recurso de GeoGebra anterior se puede establecer el Teorema de Pitágoras:
Teorema de Pitágoras
(Enunciado geométrico)
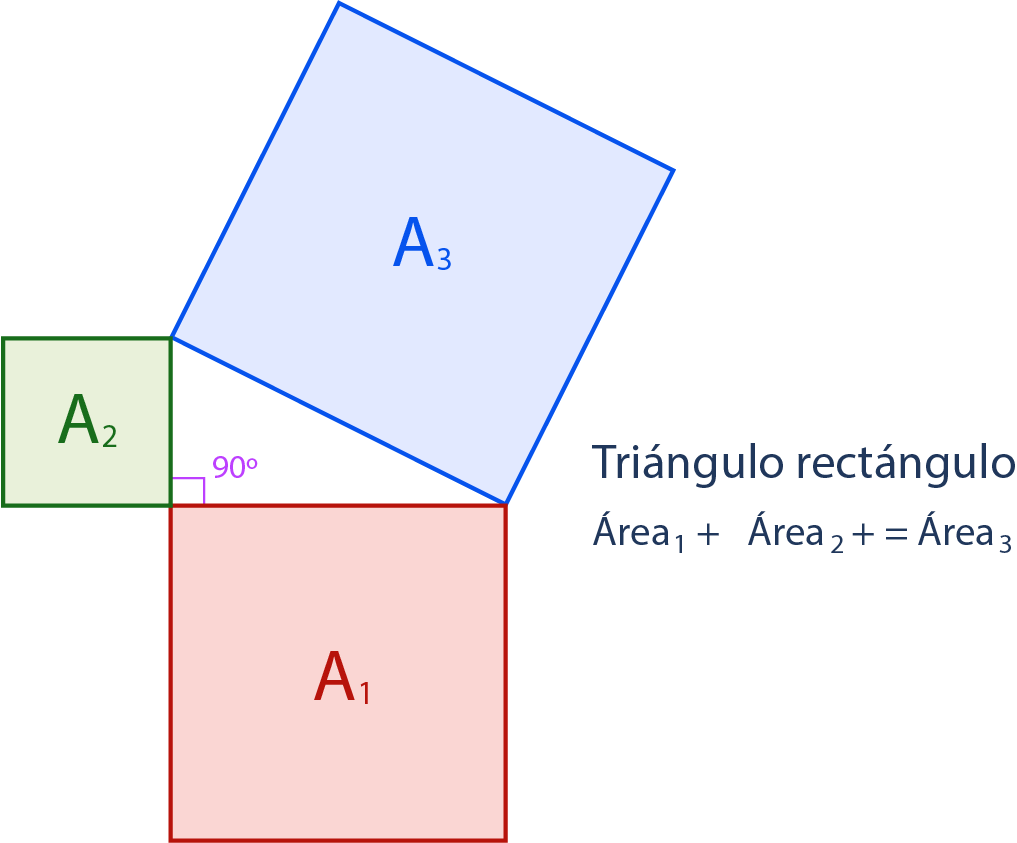
En todo triángulo rectángulo, la suma de las áreas de los cuadrados construidos sobre de los catetos es igual al área del cuadrado construido sobre la hipotenusa.
Teorema de Pitágoras
(Enunciado algebraico)
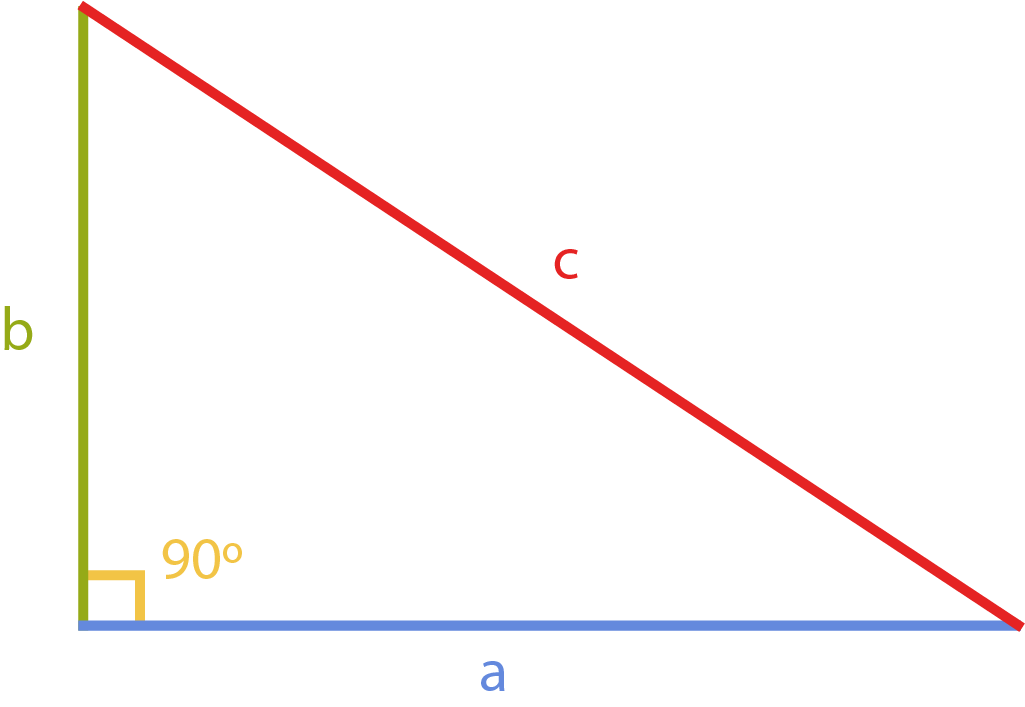
En todo triángulo rectángulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa:
$$a^2+b^2=c^2$$donde $a$ y $b$ son los catetos, $c$ es la hipotenusa.
A continuación te presentamos dos ejemplos:
En el triángulo rectángulo que tiene catetos de medida 6 cm y 8 cm, determina cuál es la medida de su hipotenusa.
Procedimiento:
| Sustituyendo los las medidas de los catetos $a=6$ y $b=8$ en el Teorema de Pitágoras se obtiene la hipotenusa $c$ del triángulo: | $c^2=a^2+b^2$ |
| $c^2=6^2+8^2$ | |
| $c^2=36+64$ | |
| $c^2=100$ | |
| $c=\sqrt{100}$ | |
| $c=10$ |
Por tanto, la hipotenusa = 10 cm
¿El triángulo que tiene lados de 4.5 cm, 6 cm y 7.5 cm es un triángulo rectángulo?
| Se sustituyen los valores dados en el Teorema de Pitágoras $c^2=a^2+b^2$ y se verifica si se cumple. | $c^2=a^2+b^2$ |
| $(4.5)^2=(6)^2+(7.5)^2$ | |
| $20.25+36=56.25$ | |
| $56.25=56.25$ |
Como sí se cumple el Teorema de Pitágoras, sí es un triángulo rectángulo.


