A continuación se presenta una tabla con los símbolos para la semejanza de triángulos:
| Símbolo | Significado |
| $∆ABC∼∆PQR$ | Los triángulos $∆ABC$ y $∆PQR$ son semejantes |
| $A\leftrightarrow P\: B\leftrightarrow Q\: C\leftrightarrow R$ | Correspondencia de vértices homólogos en los triángulos semejantes $∆PQR$ y $∆ABC$. |
| $\measuredangle A\leftrightarrow \measuredangle P\: \measuredangle B\leftrightarrow \measuredangle Q\: \measuredangle C\leftrightarrow \measuredangle R$ | Correspondencia de ángulos homólogos en los triángulos semejantes $∆PQR$ y $∆ABC$ |
| $\overline{AB}\leftrightarrow \overline{PQ}\:\overline{BC}\leftrightarrow \overline{QR}\: \overline{AC}\leftrightarrow \overline{PR}$ | Correspondencia de lados (segmentos) homólogos en los triángulos semejantes $∆PQR$ y $∆ABC$ |
| $\frac{\overline{PQ}}{\overline{AB}}=razon\:\frac{\overline{QR}}{\overline{BC}}=razon\: \frac{\overline{PR}}{\overline{AC}}=razon$ | La razón de semejanza (escala) es el cociente entre dos lados homólogos de los triángulos semejantes $∆PQR$ y $∆ABC$ |
| $\frac{\overline{AB}}{\overline{PQ}}=\frac{\overline{BC}}{\overline{QR}}=\frac{\overline{AC}}{\overline{PR}}=razon$ | Proporcionalidad de los lados homólogos en los triángulos semejantes $∆ABC$ y $∆PQR$ |
A la igualdad de dos razones se le llama una proporción, las expresiones $\frac{\overline{AB}}{\overline{PQ}}=\frac{\overline{BC}}{\overline{QR}}$, $\frac{\overline{BC}}{\overline{QR}}=\frac{\overline{AC}}{\overline{PR}}$ y $\frac{\overline{AB}}{\overline{PQ}}=\frac{\overline{AC}}{\overline{PR}}$ son ejemplos de proporciones ya que son la igualdad de dos razones. A los numeradores de cada razón se les llama antecedentes y a los denominadores consecuentes, además, en la proporción $\frac{\color{red}{\overline{AB}}}{\color{blue}{\overline{PQ}}} = \frac{\color{blue}{\overline{BC}}}{\color{red}{\overline{QR}}}$ el antecedente y el consecuente de color rojo se les llama términos extremos de la proporción y los de color azul términos medios de la proporción.
Los lados opuestos a los ángulos congruentes en triángulos semejantes son los lados homólogos, asimismo, los ángulos opuestos a los lados homólogos en los triángulos semejantes son los ángulos homólogos. En la figura los triángulos ABC y BDE son semejantes con base en esto, se te presentan sus lados y ángulos homólogos.
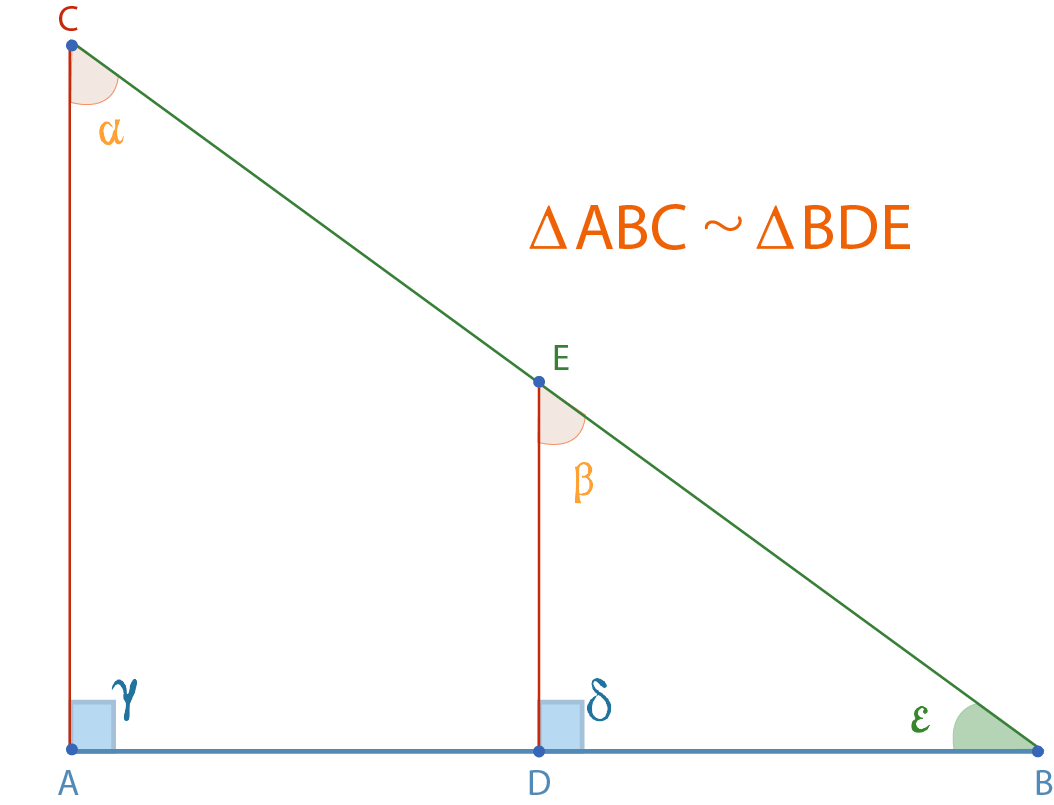
Lados y ángulos homólogos en triángulos semejantes
Lados homólogos en triángulos semejantes:
Los lados $\overline{DE}$ y $\overline{AC}$ son homólogos ya que se oponen al ángulo en común $∡ε$.
Los lados $\overline{BD}$ y $\overline{AB}$ son homólogos ya que se oponen a ángulos congruentes $∡β$ y $∡α$.
Los lados $\overline{BE}$ y $\overline{BC}$ son homólogos ya que se oponen a ángulos congruentes $∡δ$ y $∡γ$.
Ángulos homólogos en triángulos semejantes:
Los ángulos $∡α$ y $∡β$ son homólogos ya que se oponen a los lados homólogos $\overline{BD}$ y $\overline{AB}$.
Los ángulos $∡δ$ y $∡γ$ son homólogos ya que se oponen a los lados homólogos $\overline{BE}$ y $\overline{BC}$.
El ángulo $∡ε$ es homólogo a si mismo ya que se opone a los lados homólogos $\overline{DE}$ y $\overline{AC}$.
Es importante que identifiques de manera correcta los lados y ángulos homólogos en triángulos semejantes en la resolución de problemas de corte geométrico.


