En este apartado aplicarás los criterios de la semejanza de triángulos, elementos básicos de la geometría deductiva y los teoremas relacionados con las parejas de ángulos que se forman con dos rectas paralelas cortadas por una recta transversal (secante) a éstas, a la resolución de problemas y en la demostración formal para la semejanza de triángulos.
Tipos de ángulos que se forman con rectas cortadas por una recta transversal

Como recordarás los tipos de ángulos que se forman entre dos rectas cortadas por una transversal son los ángulos opuestos por el vértice, ángulos alternos internos, ángulos correspondientes, ángulos alternos externos y los ángulos adyacentes interiores del mismo lado de la transversal (ángulos interiores), para que los identifiques y recuerdes su descripción, se te presenta el siguiente recurso Geogebra .
Con base en el recurso explorarás los tipos de ángulos que se forman entre dos rectas cortadas por una recta transversal para que identifiques los tipos de ángulos que se forman con las tres rectas y recuerdes su descripción.
Luego de revisar el recurso, arrastra a la tabla las parejas de ángulos, según corresponda.
| Tipos de ángulos | Parejas de ángulos |
| Alternos-internos | |
| Correspondientes | |
| Opuestos por vértice | |
| Alternos-externos | |
| Adyacentes suplementarios |
Ángulos alternos internos: $∡d$ y $∡f$
Ángulos correspondientes: $∡a$ y $∡e$
Ángulos alternos externos: $∡b$ y $∡h$
Adyacentes suplementarios: $∡c$ y $∡f$
Teoremas sobre los ángulos que se forman entre dos rectas paralelas cortadas por una transversal (secante).

Con base en los ángulos alternos internos, correspondientes, alternos externos y adyacentes suplementarios, formularás los teoremas relacionados sobre los ángulos mencionados mediante tu interacción con el siguiente recurso Geogebra .
Con este ejercicio explorarás los tipos de ángulos que se forman entre dos rectas cortadas por una recta transversal, mediante tu interacción con el recurso, para que establezcas los teoremas relacionados con los tipos de ángulos que se forman con las tres rectas.
Ahora contesta las siguientes afirmaciones en el recuadro
Ahora con los aprendizajes sobre el concepto de la semejanza de triángulos, criterios de semejanza de triángulos y teoremas sobre los ángulos alternos internos, correspondientes, alternos externos y adyacentes suplementarios, podrás resolver problemas respecto al tema. A continuación se presenta un ejemplo y los demás problemas los resolverás en tu cuaderno y compararás tus resultados con los de la retroalimentación.
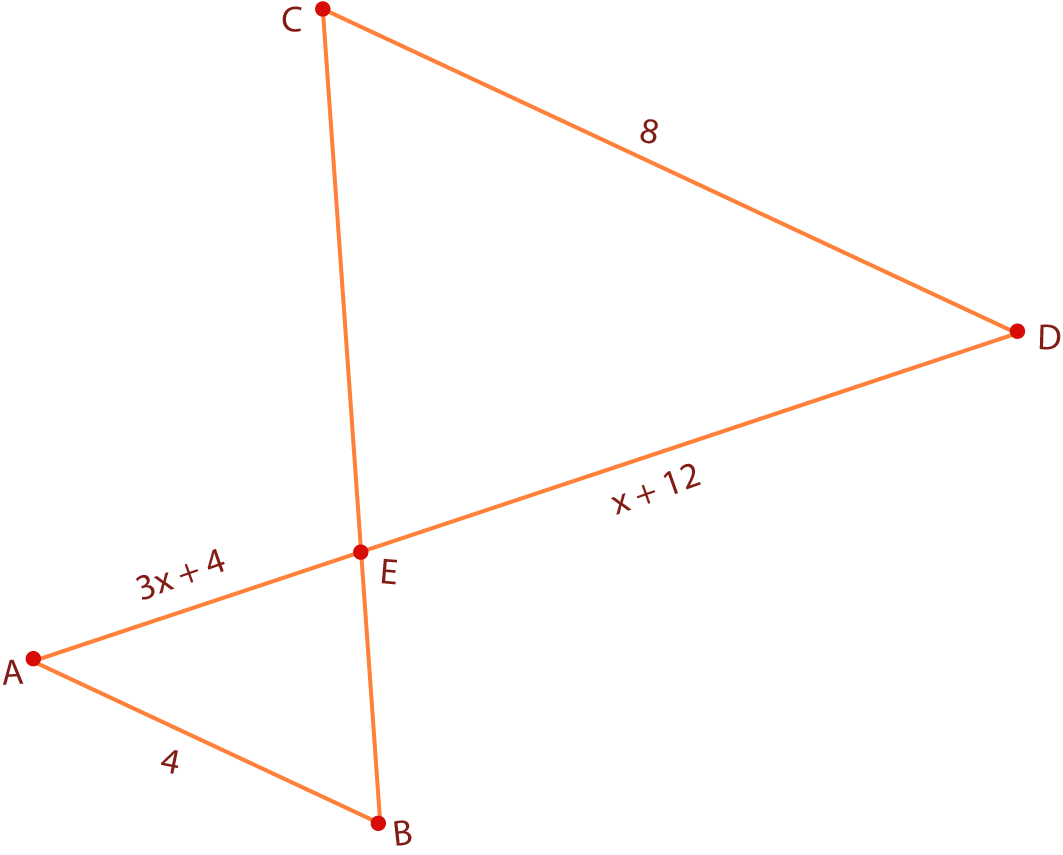
Ejemplo En la figura $\overline{AB}\parallel \overline{CD}$, $\overline{AD}$ y $\overline{BC}$ transversales, $\overline{AE}=3x+4$, $\overline{CD}=8$ y $\overline{DE}=x+12$. Con base en ésta, determina la longitud del lado $\overline{AE}$ y la longitud del lado $\overline{DE}$.
Resolución Primero demostramos que el $∆ABE∼∆CDE$.
| Afirmaciones | Razones |
| 1. $\overline{AB}\parallel \overline{CD}$, transversales $\overline{AD}$ y $\overline{BC}$ | Enunciados de los supuestos del problema. |
| 2. $\measuredangle BAE\cong\measuredangle CDE$ | Teorema sobre los ángulos alternos internos. |
| 3. $\measuredangle ABE\cong\measuredangle DCE$ | Teorema sobre los ángulos alternos internos |
| 4. $\measuredangle AEB\cong\measuredangle CED$ | Teorema sobre ángulos opuestos por el vértice. |
| 5. $\Delta ABE\sim\Delta CED$ | Criterio de semejanza de triángulos AAA. |
Esta cadena de razonamientos ejemplifica la demostración formal de $∆ABE∼∆CDE$. Este tipo de demostración es propia de la geometría deductiva a diferencia de la demostración empírica.
Como los triángulos son semejantes sus lados homólogos son proporcionales, es decir, $\frac{\overline{AB}}{\overline{CD}}=\frac{\overline{AE}}{\overline{DE}}$ y al sustituir su longitud resulta $\frac{4}{8}=\frac{3x+4}{x+12}$. Ahora como en toda proporción el producto de los extremos es igual al producto de los medios, resulta $4\left (x+12\right)=8\left( 3x+4\right)$ al eliminar paréntesis se tiene $4x+48=24x+32$, al agrupar los términos con $x$ al lado derecho de la ecuación se tiene $48-32=24x-4x$, al simplificar queda $16=20x$ y al despejar $x$ se obtiene $x=\frac{4}{5}$.
Ahora $\overline{AE}=3x+4=3\left(\frac{4}{5}\right )=\frac{12}{5}+\frac{20}{5}=\frac{32}{5}$
Al sustituir $x=\frac{4}{5}$ en $\overline{DE}$ se tiene $\overline{DE}=x+12=\frac{4}{5}+\frac{60}{5}=\frac{64}{5}$
A continuación resuelve los siguientes problemas.
En la figura $∆BB'P∼∆AA'P$, además, $\overline{A{A}'}=2.48\: m$, $\overline{{A}'P}=3.01\: m$ y $\overline{{B}'P}=11.5\: m$. Determina la altura del árbol $\overline{B{B}'}=x$ y escríbela en el recuadro:
Sugerimos que para la resolución del problema, escribas en tu cuaderno la proporción de los lados homólogos de los triángulos semejantes y despejes el valor de la incógnita x , como se mostró en el ejemplo anterior.
La figura incluye verticalmente un edifico, un farol y una joven, $\overline{AC}\parallel \overline{DE}$ y $\overline{BD}$ transversal a ellas, considera los datos de ésta y determina lo que se te pide:
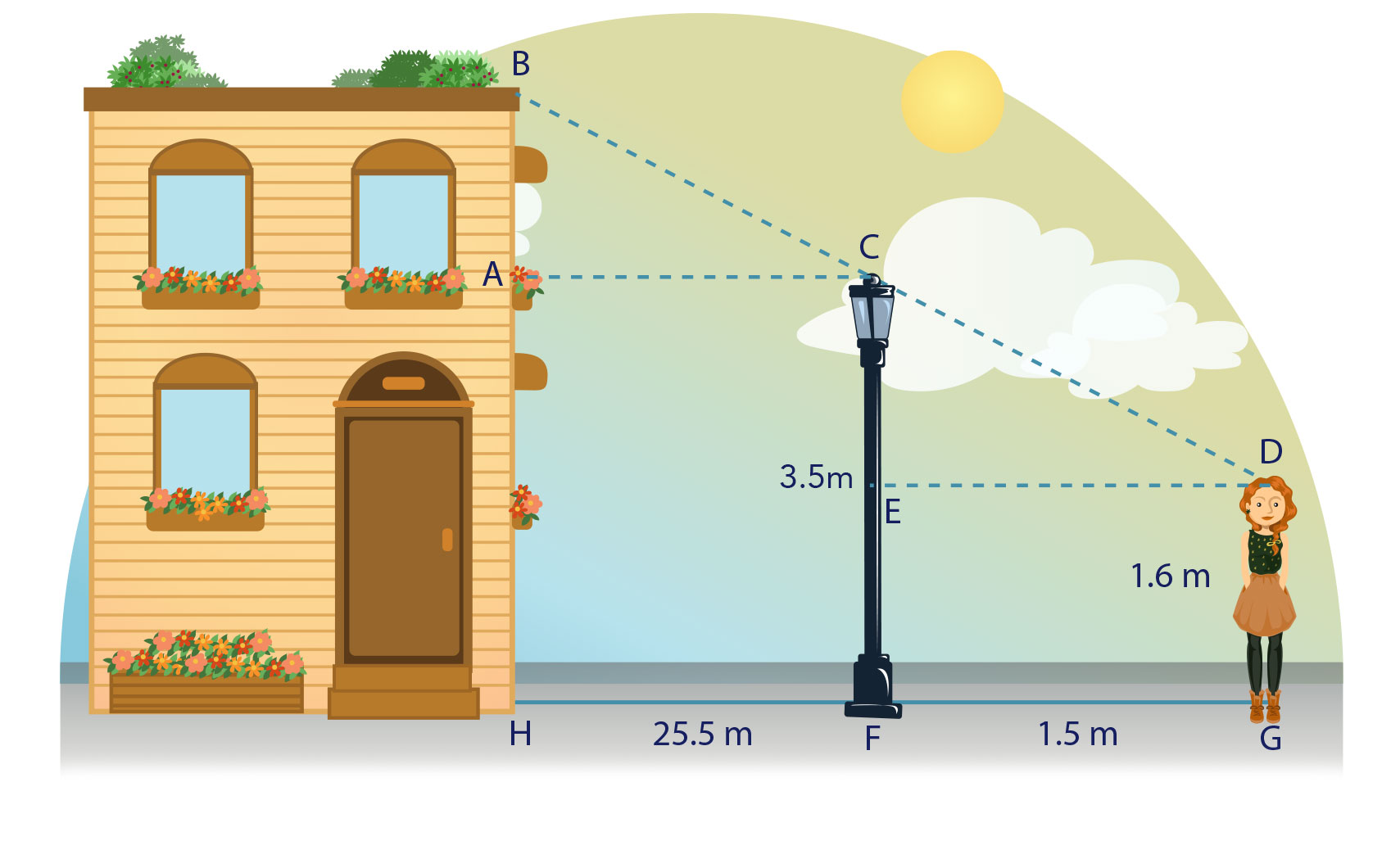
a) Demuestra que $∆ABC∼∆CDE$. Para ello, arrastra en la tabla las afirmaciones o razones, según corresponda.
Demostración
| Afirmaciones | Razones |
| 1) $\overline{AC}\parallel \overline{ED}$ y la recta $\overline{BD}$ transversal a ellas | Enunciado de los supuestos del problema |
| 2) | Teorema sobre ángulos correspondientes |
| 3) $\overline{BH}\parallel \overline{CF}$ y la recta $\overline{BD}$ transversal a ellas | |
| 4) | Teorema sobre ángulos correspondientes |
| 5) $\measuredangle BAC\cong \measuredangle CED=90^{\circ}$ | |
| 6) | Criterio de semejanza de triángulos AAA |
Como ${\overline{AC}\parallel \overline{HG}}$ y la recta ${\overline{BD}}$ es una transversal a ellas por el teorema de los ángulos correspondientes que ${\measuredangle CDE\cong \measuredangle BCA}$, asimismo, como ${\overline{BH}\parallel \overline{CF}}$ y la recta ${\overline{BD}}$ es una recta transversal a ellas se tiene que ${\measuredangle ABC\cong \measuredangle DCE}$ y dado que las rectas ${\overline{BH}\parallel \overline{CF}}$ y además perpendiculares a la recta ${\overline{HG}}$, el ${\measuredangle BAC\cong \measuredangle CED=90^{\circ}}$.
Esta cadena de razonamientos demuestra que los ángulos homólogos de los triángulos son congruentes, es decir, $∡CDE≅∡BCA$, $∡ABC≅∡DCE$ y $∡BAC≅∡CED$, por lo que al aplicar el teorema de la semejanza de triángulos AAA se tiene que $∆ABE∼∆CDE$.
En la siguiente figura $\overline{AC}\perp \overline{AD}$, $\overline{DE}\perp \overline{AD}$, $\overline{AB}=8\: m$, $\overline{BD}=6\: m$ y $\overline{DE}=12\: m$.
a) Demuestra que $∆ABC∼∆BDE$. Para ello, arrastra a la tabla las afirmaciones o razones, según corresponda.
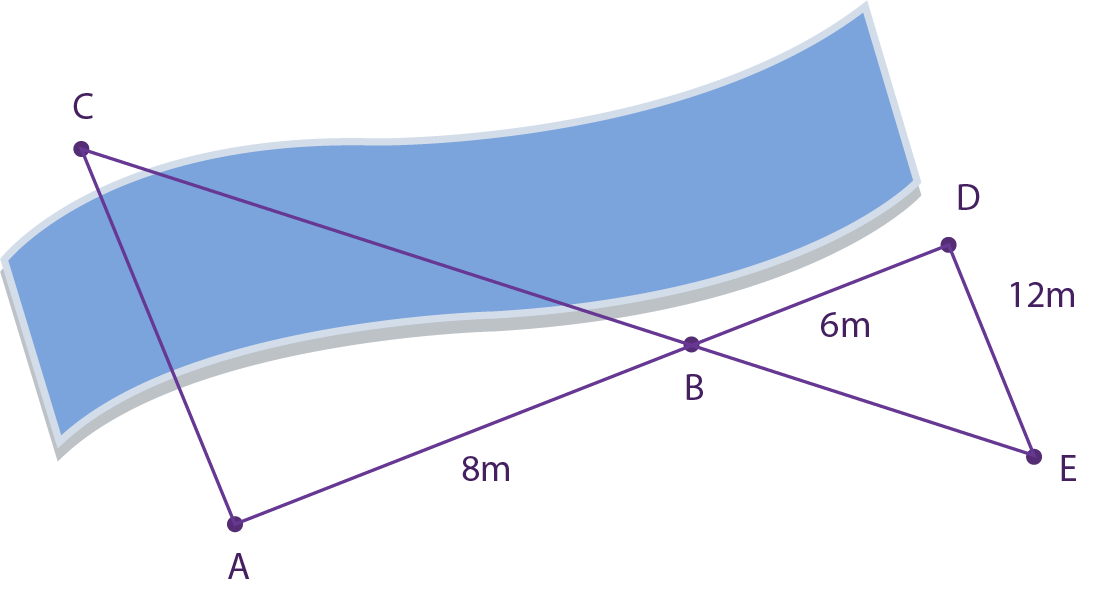
Demostración
| Afirmaciones | Razones |
| 1) $\measuredangle BAC\cong \measuredangle BDE=90^{\circ}$ | Por hipótesis $\overline{AC}\perp \overline{AD}$ y $\overline{DE}\perp \overline{AD}$ |
| 2) | Teorema. Los ángulos opuestos por el vértice son congruentes |
| 3) $\measuredangle BAC+\measuredangle ABC+\measuredangle ACB=180^{\circ}$ | |
| 4) $\measuredangle BDE+\measuredangle DBE+\measuredangle BED=180^{\circ}$ | Teorema. Los ángulos internos de un triángulo suman 180° |
| 5) $\measuredangle BAC+\measuredangle ABC+\measuredangle ACB=$ $\measuredangle BDE+\measuredangle DBE+\measuredangle BED$ | Axioma. Dos cantidades iguales a una tercera son iguales entre sí |
| 6) | Axioma. Si a cantidades iguales se les resta otras también iguales los totales son iguales |
| 7) $\Delta ABC\sim \Delta BDE$ |
Afirmación: 2. $∡ABC≅∡DBE$
Razón 3: Teorema. Los ángulos internos de un triángulo suman $180°$
Afirmación 6. $∡ACB≅∡BED$
Razón 7: Teorema de semejanza de triángulos AAA
Fin de la actividad


