Deducción del Teorema de Thales

En este apartado se explica el teorema de Thales y su demostración formal. Cabe mencionar que a las afirmaciones del teorema se le llama hipótesis , lo que se quiere demostrar se llama tesis y la cadena de razonamientos lógicos sustentados por definiciones, postulados, axiomas y teoremas ya demostrados, se le llama demostración.

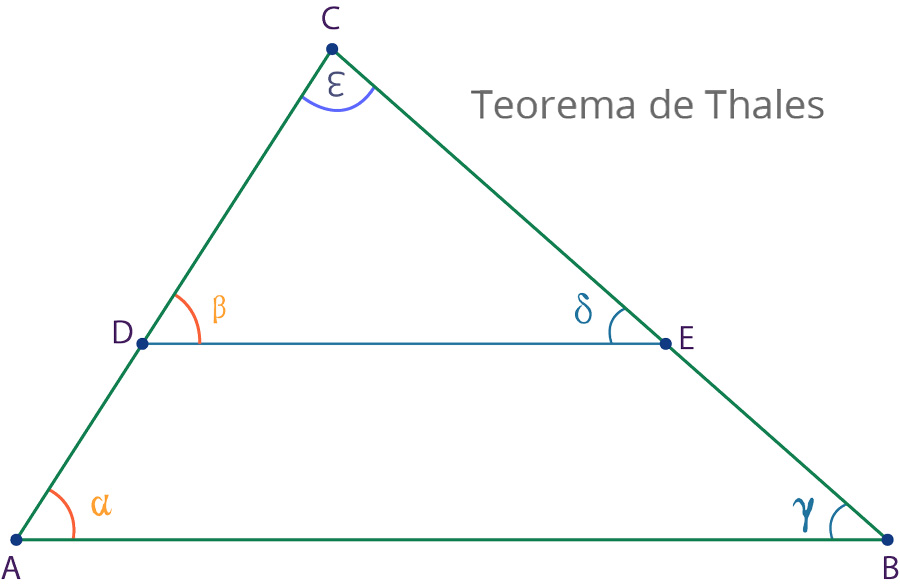
Enunciado del teorema de Thales

Toda recta paralela a uno de los lados de un triángulo divide a los otros dos lados en partes proporcionales.

A continuación, escribe en la tabla el número de las afirmaciones o razones, según corresponda para la demostración del teorema mencionado:

Hipótesis del teorema de Thales Tesis del teorema
∆ABC es un triángulo
$\overline{DE}\parallel \overline{AB}$		 ${\frac{\overline{CD}}{DA}=\frac{\overline{CE}}{EB}}$

1. Teorema. Criterio de semejanza $AAA$

2. ${\frac{\overline{CD}}{CA}=\frac{\overline{CE}}{CB}}$

3. Axioma. Si a cantidades iguales se les resta otras también iguales, los totales son iguales.

Demostración

Afirmaciones Razones
1) $\Delta DEC\sim \Delta ABC$
2) Definición de triángulos semejantes. Lados homólogos de triángulo semejantes son proporcionales. Proporción del ∆DEC al ∆ABC.
3) $\frac{\overline{CA}}{\overline{CD}}=\frac{\overline{CB}}{\overline{CE}}$ Teorema. En toda proporción se pueden cambiar los antecedentes por sus respectivos consecuentes.
4) $\frac{\overline{CD}+\overline{DA}}{\overline{CD}}=\frac{\overline{CE}+\overline{EB}}{\overline{CE}}$ Axioma. El todo es la suma de sus partes.
5) $\frac{\overline{CD}}{\overline{CD}}+\frac{\overline{DA}}{\overline{CD}}=\frac{\overline{CE}}{\overline{CE}}+\frac{\overline{EB}}{\overline{CE}}$ Axioma. Toda cantidad puede sustituirse por su igual.
6) $1+\frac{\overline{DA}}{\overline{CD}}=1+\frac{\overline{EB}}{\overline{CE}}$ Axioma. Toda cantidad puede sustituirse por su igual.
7) $\frac{\overline{DA}}{\overline{CD}}=\frac{\overline{EB}}{\overline{CE}}$
8) $\frac{\overline{CD}}{\overline{DA}}=\frac{\overline{CE}}{\overline{EB}}$ Teorema. En toda proporción se pueden cambiar los antecedentes por sus respectivos consecuentes.
Esta es la tesis que se quería demostrar.

Esta cadena de razonamientos demuestra que toda paralela al tercer lado de un triángulo divide a los otros dos en partes proporcionales.

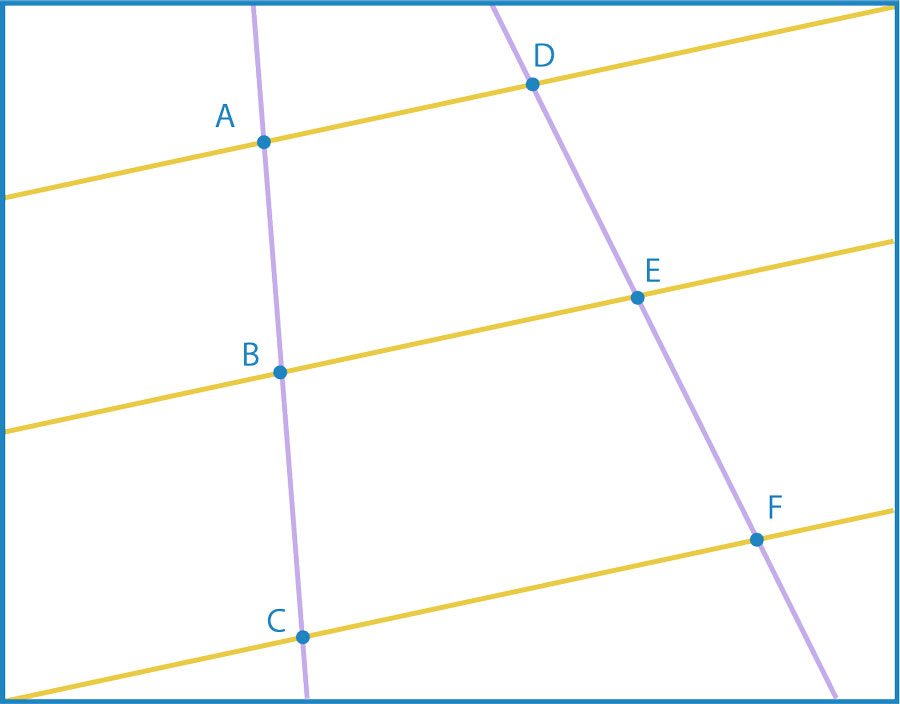
El teorema de Thales que acabas de demostrar también puede ser enunciado de la siguiente manera, si dos o más rectas paralelas son cortadas por dos rectas transversales a ellas, entonces las longitudes de los segmentos interceptados entre las rectas paralelas y cada una de las transversales son proporcionales. En la figura $\overleftrightarrow{AD}\parallel \overleftrightarrow{BE}\parallel\overleftrightarrow{CF}$ y las rectas $\overleftrightarrow{AC}$ y $\overleftrightarrow{BF}$ transversales a ellas, lo que afirma el teorema de Thales es que los segmentos interceptados por las rectas transversales en cada una de las paralelas son proporcionales, es decir, $\frac{\overline{AB}}{\overline{BC}}=\frac{\overline{DE}}{\overline{EF}}$

Ahora se te presentan dos ejemplos de la aplicación del Teorema de Thales

En la figura $\overline{BD}=5.32$cm, $\overline{CD}=4.46$cm, $\overline{DE}\parallel \overline{AB}$ y la longitud de $\overline{AC}=11.65$cm. Obtén la longitud de los segmentos $\overline{AE}$ y $\overline{CE}$.

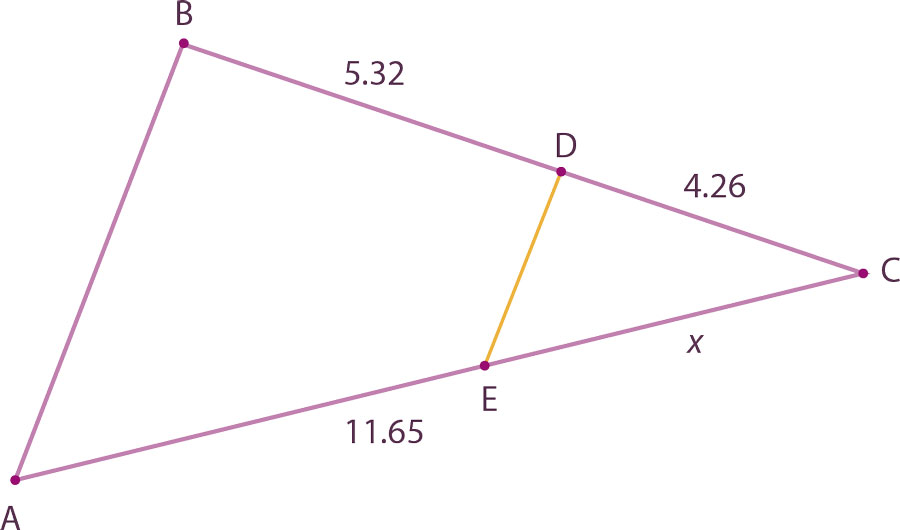
Como $\overline{DE}\parallel \overline{AB}$ por el teorema de Thales se tiene que $\frac{4.26}{5.32}=\frac{x}{11.65-x}$

En toda proporción el producto de los extremos es igual al producto de los medios $4.26(11.65-x)=5.32x$

Al eliminar el paréntesis $49.629-4.26x=5.32x$

Agrupando los términos que contienen a x al lado derecho de la ecuación $49.629=5.32x+4.26x $

Simplificando el lado derecho de la ecuación $49.629=9.58x$

Despejando la variable $x$, $\frac{49.629}{9.58}=x$

Resultado de la división $5.18=x$, por lo que $\overline{CE}=5.18$cm.

Ahora al sustituir $x=5.18$ en $\overline{AE}=11.65-x$ y realizar operaciones se obtiene $\overline{AE}=11.65-x=11.65-5.18=6.47$cm, por lo que $\overline{AE}=6.47$cm.

En la figura las rectas $\overleftrightarrow{BC}\parallel \overleftrightarrow{DE}\parallel\overleftrightarrow{FG}$, las rectas $\overleftrightarrow{AF}$ y $\overleftrightarrow{AG}$ son transversales a éstas, $\overline{BD}=3.67 cm$, $\overline{DF}=4.99 cm$, $\overline{AC}=5.21 cm$ y $\overline{EG}=5.52 cm$. Determina la longitud de los segmentos $a$ y $d$.

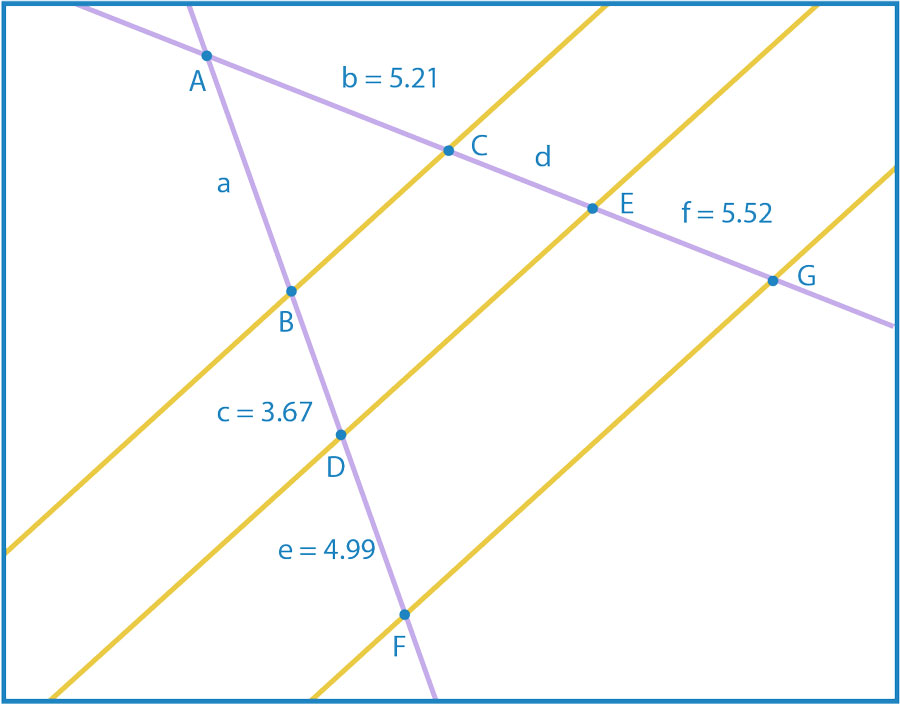
Solución. Como las rectas $\overleftrightarrow{BC}\parallel \overleftrightarrow{DE}\parallel\overleftrightarrow{FG}$ y las rectas $\overleftrightarrow{AF}$ y $\overleftrightarrow{AG}$ son transversales a éstas, se aplica el teorema de Thales.

Los segmentos interceptados en las rectas paralelas son proporcionales $\frac{3.67}{4.99}=\frac{d}{5.52}$

En toda proporción el producto de los extremos es igual al producto de los medios $4.99d=3.67(5.52)=20.2584$

Al despejar la variable d y realizar la división se obtiene $d=\frac{20.2584}{4.99}=4.05$cm

Los segmentos interceptados en las rectas paralelas son proporcionales $\frac{a}{3.67}=\frac{5.21}{4.05}$

En toda proporción el producto de los extremos es igual al producto de los medios $4.05a=3.67(5.21)=19.1207$

Al despejar la variable $a$ y realizar la división se obtiene $a=\frac{19.1207}{4.05}=4.72$cm