El estudio de la geometría se remonta hasta las culturas antiguas (Babilonia, Mesopotamia y Egipto), originada por las necesidades prácticas de sus pobladores, como la medida de la tierra destinada a la agricultura, construcción de sistemas de drenaje para contrarrestar las inundaciones (babilonios y mesopotámicos), así como, edificios y monumentos emblemáticos, por ejemplo, las pirámides de Keops (egipcios), entre otras. La medida de la tierra de cultivo y las construcciones mencionadas muestran que las culturas antiguas tenían conocimientos sólidos de figuras geométricas. A esta geometría se le conoce como geometría empírica (práctica), por surgir como necesidades cotidianas de las culturas mencionadas. Esta geometría fue retomada por los griegos dándole una orientación de geometría deductiva, basada en una cadena de razonamientos lógicos sustentados por definiciones de objetos geométricos, postulados, axiomas y teoremas.

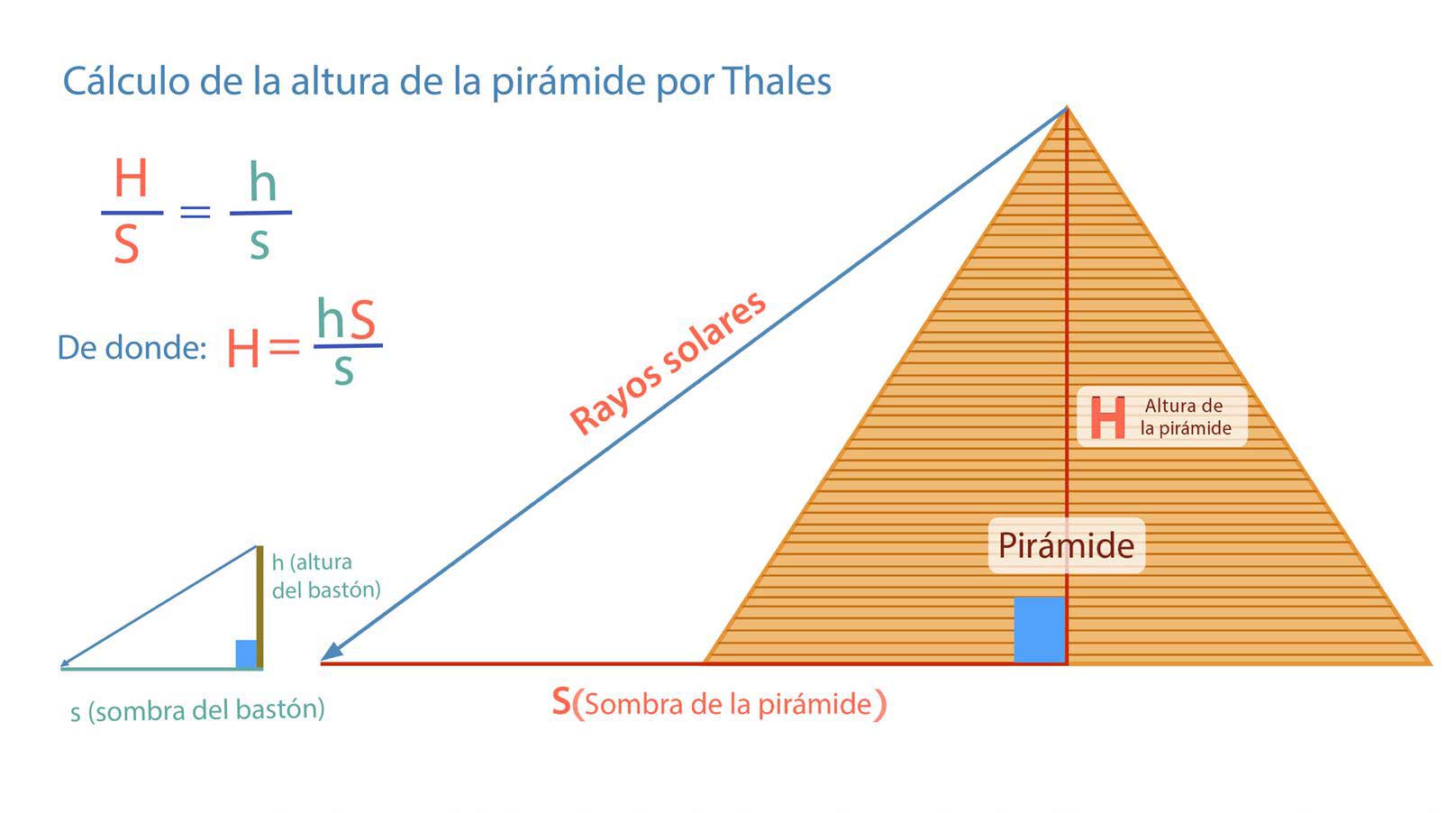
El primero de los geómetras griegos que desarrolló la geometría con una orientación deductiva fue Thales de Mileto y debido a sus aportaciones filosóficas, científicas y matemáticas, lo consideraron como uno de los siete sabios de la antigüedad. El segundo geómetra que realizó aportaciones relevantes al desarrollo de la ciencia fue Pitágoras discípulo de Thales, dentro de sus desarrollos en la geometría se encuentra el teorema que lleva su nombre y su demostración formal.
Aunado a los trabajos realizados por lo geómetras griegos mencionados, se encuentra la aportación del tercer del geómetra griego Euclides con el desarrollo de su obra Los Elementos en una colección de 13 tomos, de éstos los seis primeros están dedicados a la geometría deductiva.
En este objeto de aprendizaje estudiarás la semejanza de figuras geométricas para que comprendas sus características, en particular, la semejanza de triángulos y su representación simbólica, los criterios de semejanza y su demostración de forma empírica, así como, su aplicación en la demostración de teoremas y en la resolución de problemas de corte geométrico, además, del procedimiento para la división de un segmento para un número n de partes iguales, dando entrada a la formulación del teorema de Thales y su demostración formal, así como, su aplicación en la resolución de problemas de corte geométrico.


