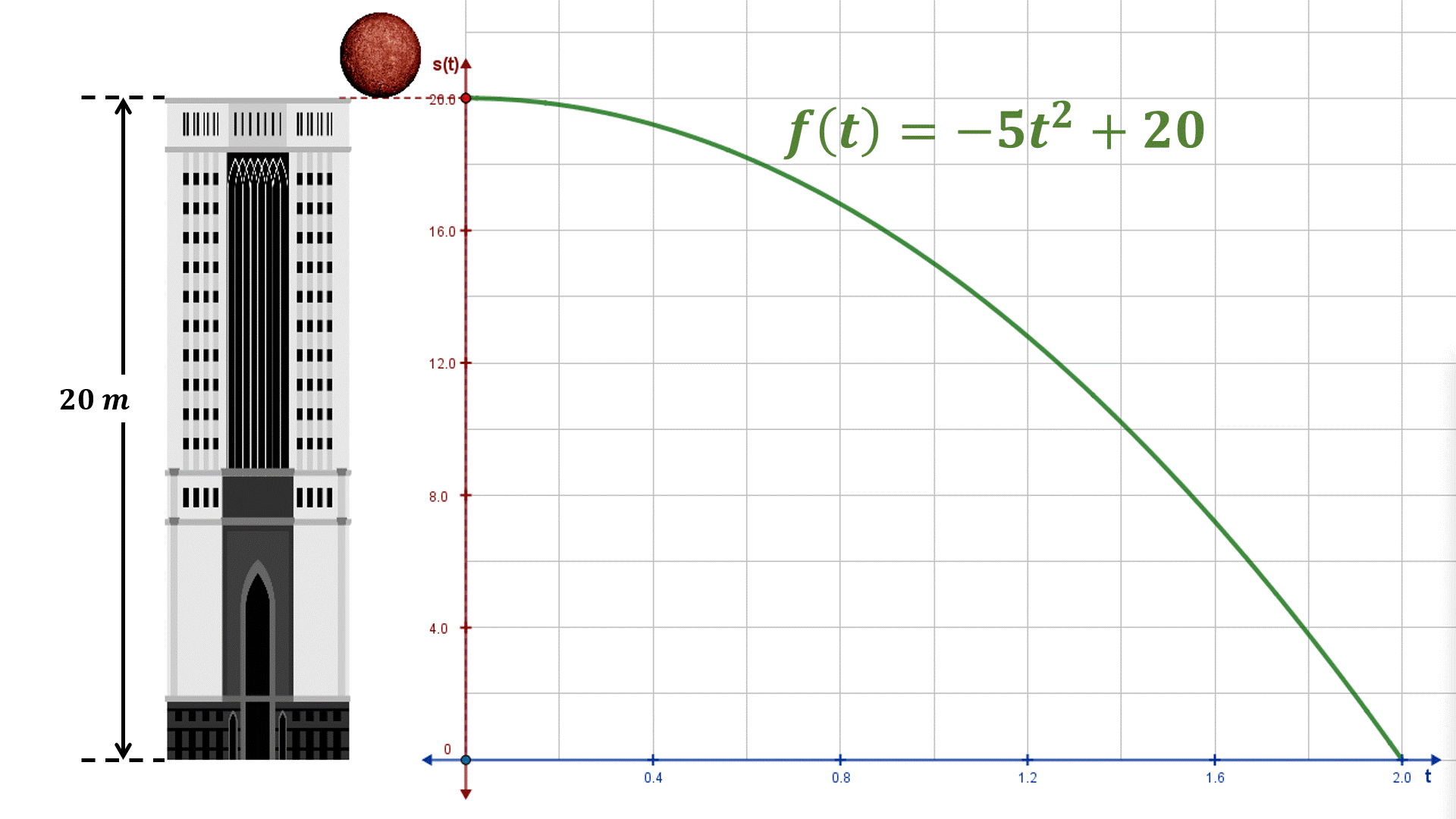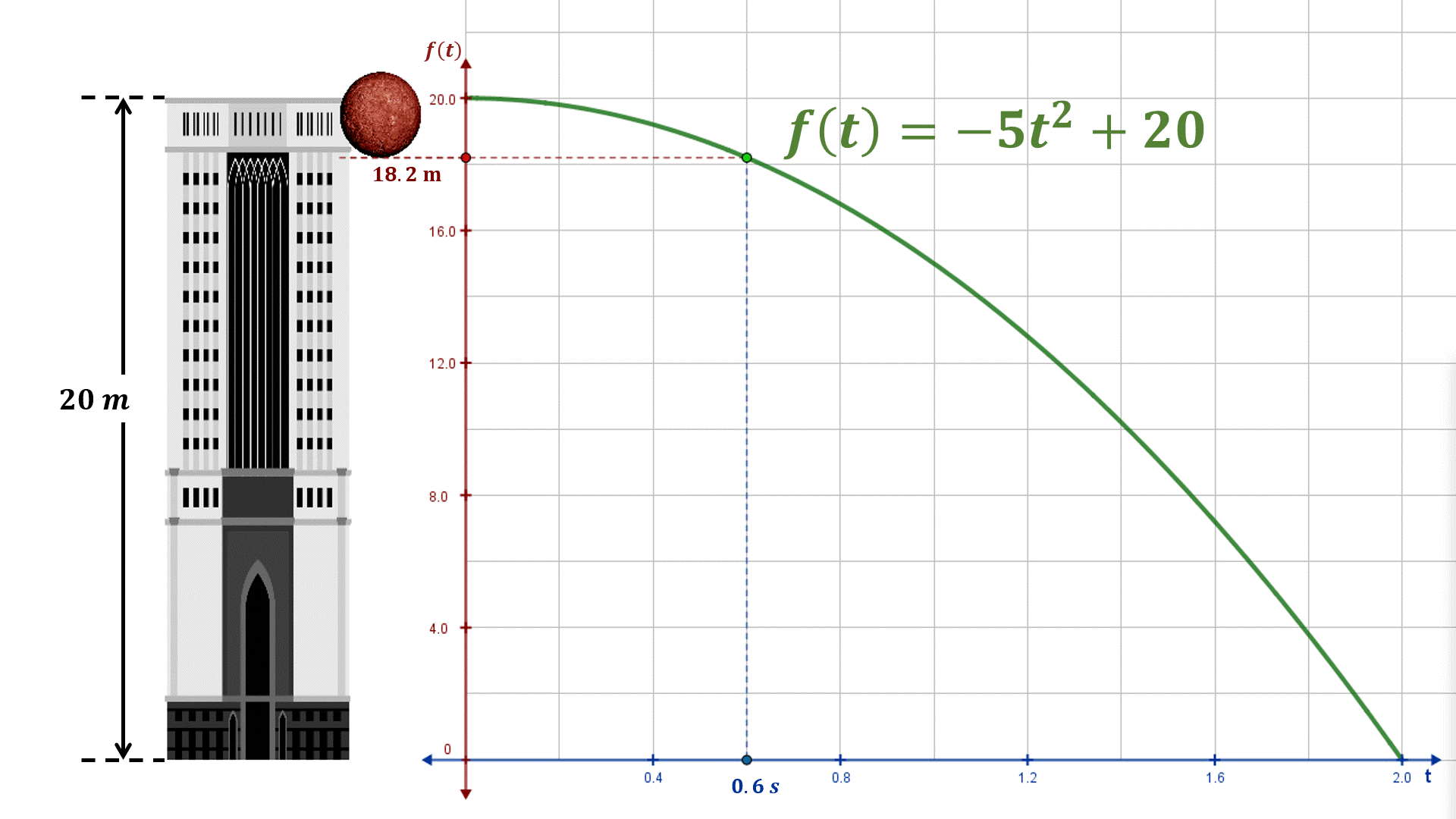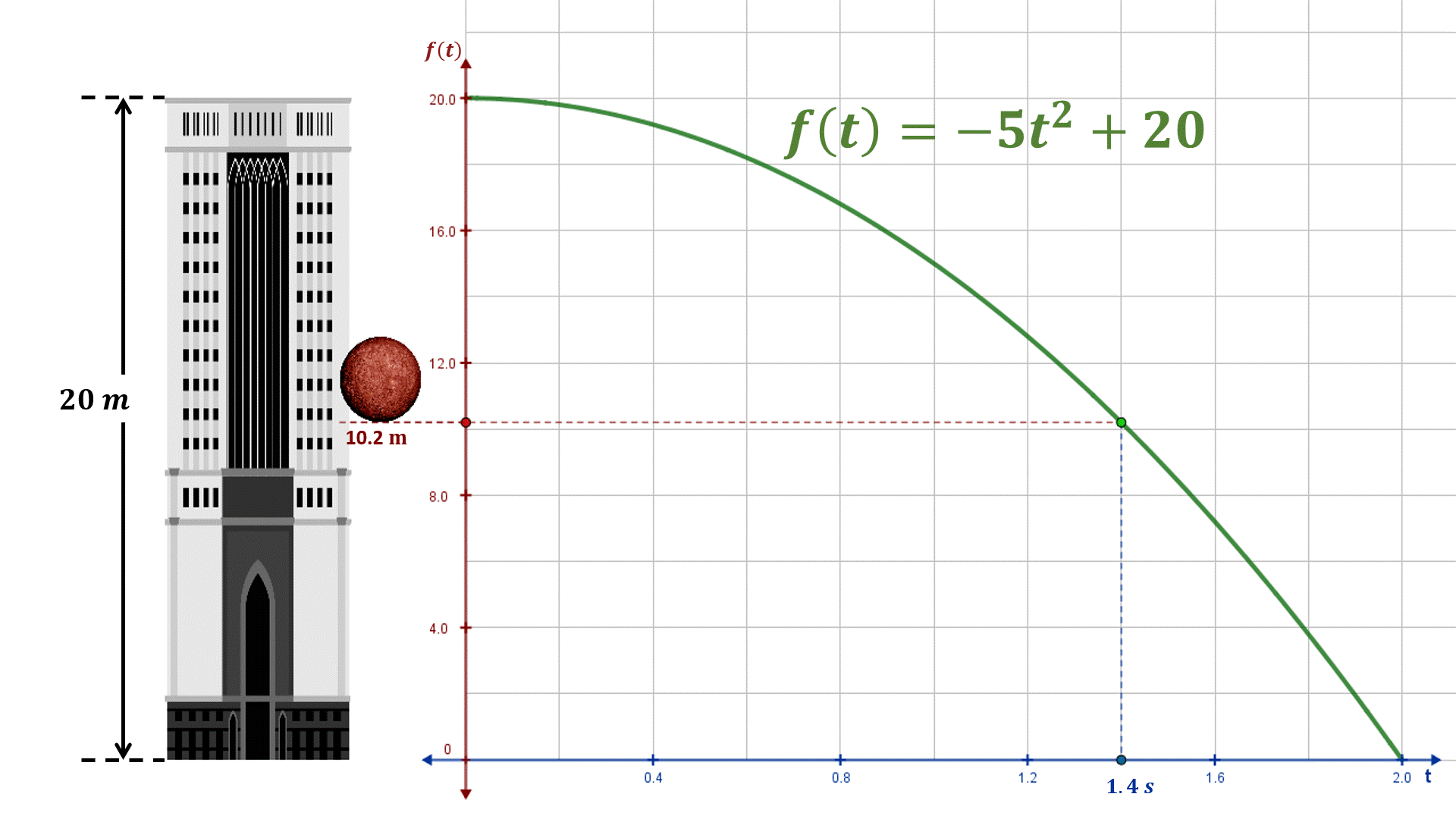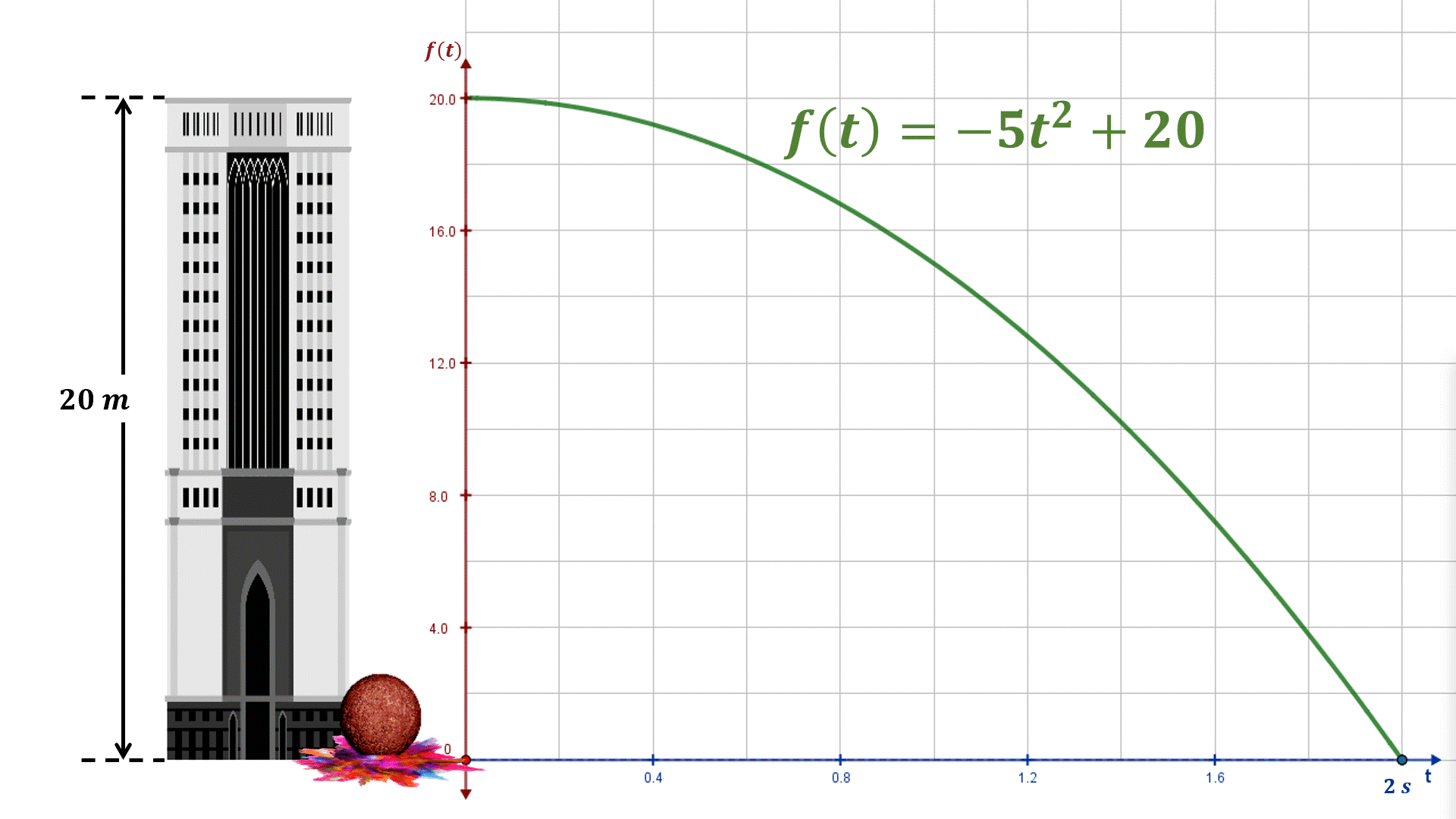El ejemplo de la pantalla anterior tiene como objetivo ofrecerte un primer acercamiento al concepto de la derivada, y a la importancia de su estudio. Dicho concepto fue desarrollado por varios matemáticos de la antigüedad, entre ellos, Leibniz (1646-1716) y Newton (1642-1727); el primero desarrolló el concepto de la derivada mediante el estudio de las rectas tangentes; y el segundo mediante el estudio de la velocidad; Lagrange (1736-1813) y Cauchy (1789-1857) también hicieron aportaciones importantes.
Cabe mencionar que estos matemáticos propusieron notaciones diferentes para la derivada; Newton la representó mediante el límite $\dot y = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {a + h} \right) - f(a)}}{h}$; en la notación de Leibniz se utiliza la razón $\frac{{dy}}{{dx}}$; Lagrange la representó como $y'$; mientras que Cauchy utilizó la notación ${D_x}{\rm{ }}f\left( x \right)$.
En el objeto de aprendizaje «Variación y razón de cambio promedio e instantánea de una función», se hace el análisis de la definición de Fermat y con ella obtienen las derivadas de diversas funciones polinomiales. Te invitamos a que revises dicho material para que profundices en el aprendizaje de esta definición.
Definición de la derivada de Fermat
La derivada de una función $f$ en un número fijo $a$, denotada por $f'\left( a \right)$, es:
$f'\left( a \right) = \mathop {\lim }\limits_{x \to a} \frac{{f\left( x \right) - f(a)}}{{x - a}}$
siempre que el límite exista.
Geométricamente es el valor de la pendiente de la recta tangente a la gráfica de la función en el punto $P\left( {a,f\left( a \right)} \right)$.
Existe otra definición de derivada, llamada definición de Newton $f'\left( x \right) = \mathop {\lim }\limits_{x \to a} \frac{{f\left( {x + h} \right) - f(x)}}{h}$, que a veces es más fácil utilizar. En esta definición se considera que $h = x - a$ y, por lo tanto, $x = a + h$; estas expresiones indican que $h$ tiende a cero sí y sólo sí $x$ tiende a $a$. En consecuencia, la definición de derivada se puede reescribir de la siguiente manera:
Definición de la derivada de Newton
La derivada de una función $f$ en un número fijo $a$, denotada por $f'\left( a \right)$, es:
$f'\left( a \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {a + h} \right) - f(a)}}{h}$
siempre que el límite exista.
Geométricamente es el valor de la pendiente de la recta tangente a la gráfica de la función en el punto $P\left( {a,f\left( a \right)} \right)$.
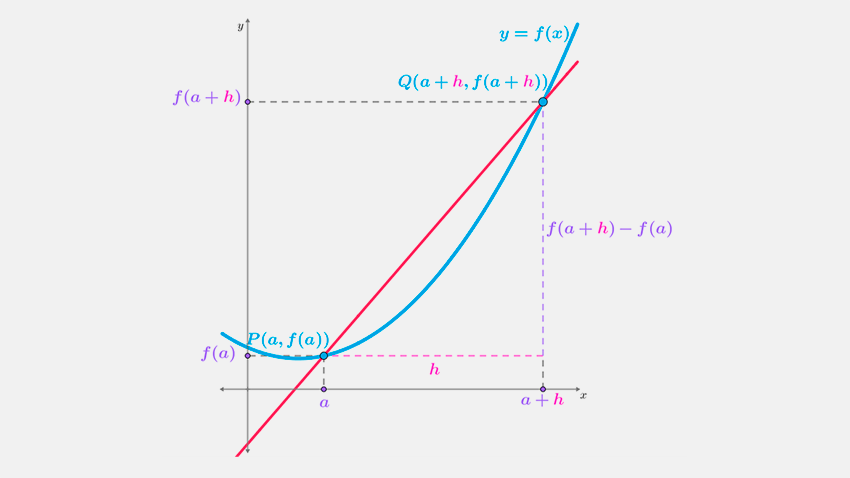
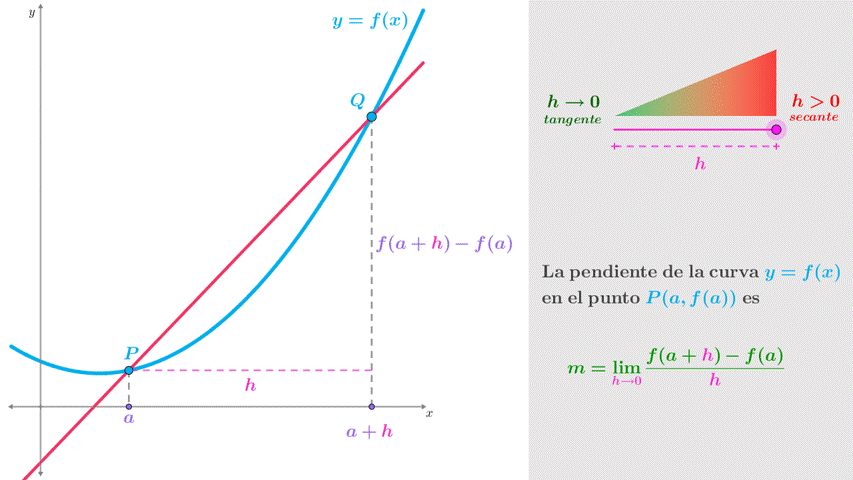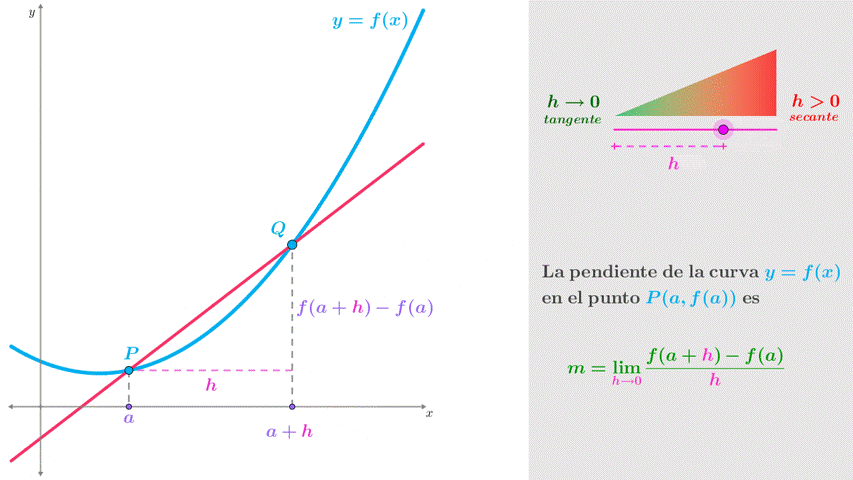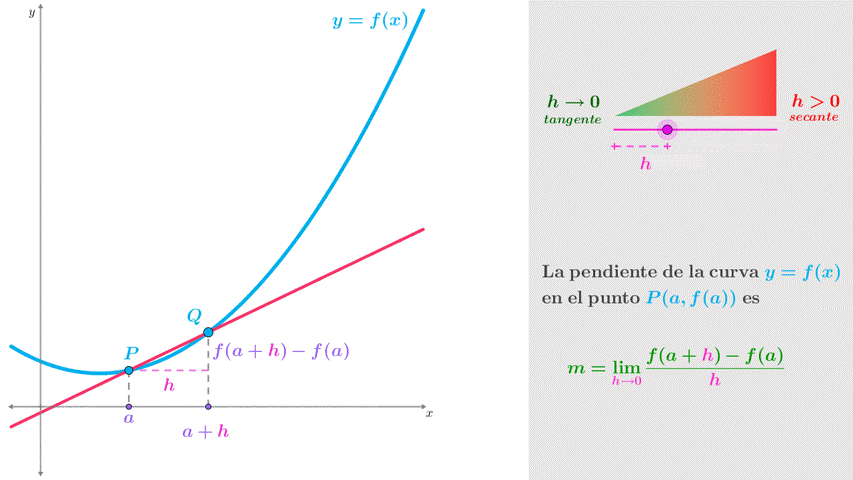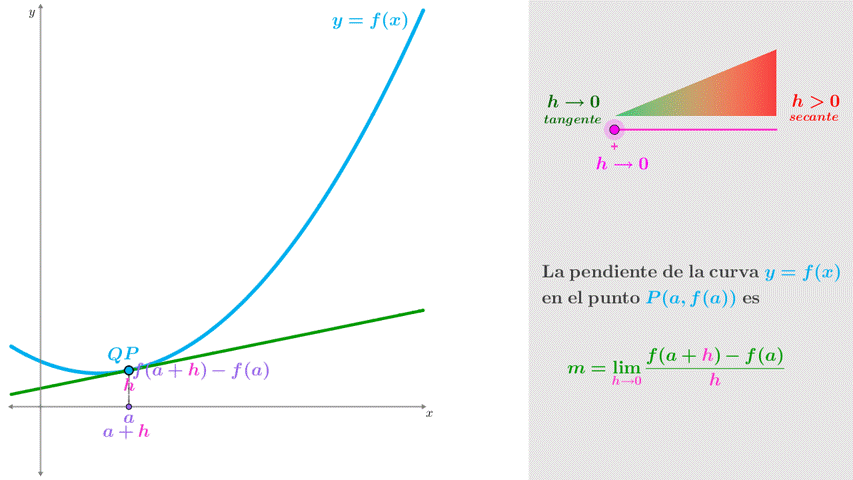
En la figura 2a se muestra la curva $\color{Cyan}{y = f\left( x \right)}$ y la recta secante que pasa por los puntos $P\left( {a,f\left( a \right)} \right)$ y $\color{Cyan}{Q\left( {a + h,f\left( {a + h} \right)} \right)}$. Observa que la distancia entre $\color{Cyan}{P}$ y $\color{Cyan}{Q}$ está determinada por el valor de $\color{Magenta}{h}$; conforme el valor de $\color{Magenta}{h}$ decrementa y tiede a cero $\color{Magenta}{h \to 0}$, la recta secante tiende a la recta tangente en el punto $\color{Cyan}{P}$ (figura 2b).
La pendiente $\color{OliveGreen}{m_{PQ}}$ de la recta secante se obtiene de la razón entre la diferencia de ordenadas y la diferencia de abscisas, es decir,
$\color{OliveGreen}{{m_{PQ}} = \frac{{f\left( {a + h} \right) - f(a)}}{{\left( {a + h} \right) - \left( a \right)}} = \frac{{f\left( {a + h} \right) - f(a)}}{h}}$
Ahora bien, la pendiente $\color{OliveGreen}{m}$ de la recta tangente se determina en el límite donde $h \to 0$, es decir
$\color{OliveGreen}{m = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {a + h} \right) - f(a)}}{h}}$
Si el límite existe, la expresión anterior representa la pendiente de la curva en el punto $P$. A este límite se le conoce como la derivada de la función $f$ en el número $a$ y se representa con la notación $f'\left( a \right)$, y corresponde a la definición de derivada de Newton.
En los siguientes ejemplos utilizarás las definiciones de Fermat y de Newton para calcular las derivadas de funciones polinomiales.
-
Derivada de una función constante
Ejemplo 1. Desde diciembre de 2013, el costo del boleto del Metro de la Ciudad de México es de 5 pesos. La función constante $f\left( t \right) = 5$ representa el costo del boleto en los últimos años, donde $t$ es el tiempo; el costo se expresa en pesos y el tiempo en meses. A continuación, determinaremos la derivada de la función constante en el instante ${t_0} = a = 20$, utilizando las definiciones de Newton y de Fermat.
 Figura 3. Boleto conmemorativo (Fundación UNAM, 2017).
Figura 3. Boleto conmemorativo (Fundación UNAM, 2017).Solución 1. Utilizando la definición de Fermat $\begin{array}{l} f'\left( a \right) = \mathop {\lim }\limits_{t \to a} \frac{{f\left( t \right) - f(a)}}{{t - a}}\\ f'\left( {20} \right) = \mathop {\lim }\limits_{t \to 20} \frac{{20 - 20}}{{t - 20}}\\ f'\left( {20} \right) = \mathop {\lim }\limits_{t \to 20} \frac{0}{{t - 20}}\\ f'\left( {20} \right) = \mathop {\lim }\limits_{t \to 20} 0\\ f'\left( {20} \right) = 0 \end{array}$ Solución 2. Utilizando la definición de Newton $\begin{array}{l} f'\left( a \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {a + h} \right) - f\left( a \right)}}{h}\\ f'\left( {20} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{20 - 20}}{h}\\ f'\left( {20} \right) = \mathop {\lim }\limits_{h \to 0} \frac{0}{h}\\ f'\left( {20} \right) = \mathop {\lim }\limits_{h \to 0} 0\\ f'\left( {20} \right) = 0 \end{array}$ Como pudiste observar, la derivada de la función es $f'\left( {20} \right) = 0$. En este ejemplo, la derivada indica la razón de cambio instantánea del precio respecto al tiempo; el valor cero indica que no hubo variación del precio en el tiempo.
-
Derivada de una función lineal
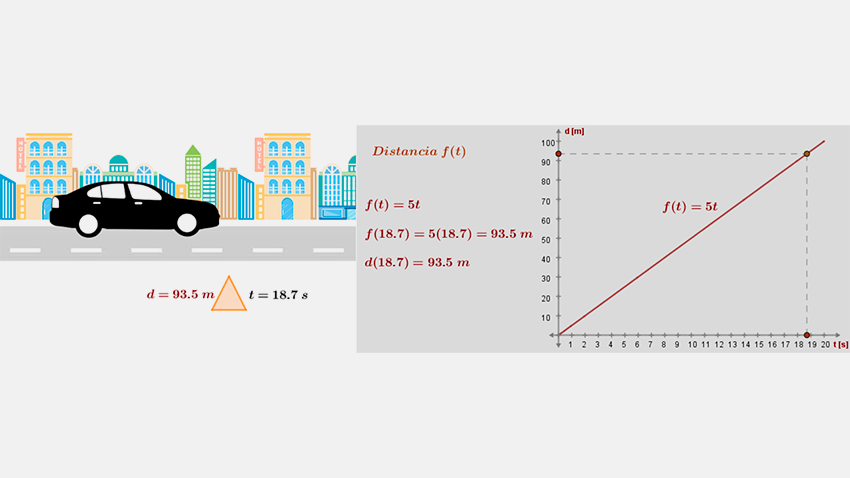
Ejemplo 2. En la imagen se muestra un automóvil con movimiento rectilíneo uniforme cuya función de desplazamiento es $f\left( t \right) = 5t$, donde $t$ es la variable independiente y representa el tiempo; el desplazamiento se expresa en metros y el tiempo en segundos.
A continuación, determinaremos la derivada de la función lineal en el instante ${t_0} = a = 18.7$, utilizando las definiciones de Fermat y de Newton.
Solución 1. Utilizando la definición de Fermat $\begin{array}{l} f'\left( a \right) = \mathop {\lim }\limits_{t \to a} \frac{{f\left( t \right) - f(a)}}{{t - a}}\\ f'\left( {18.7} \right) = \mathop {\lim }\limits_{t \to 18.7} \frac{{f\left( t \right) - f\left( {18.7} \right)}}{{t - 18.7}}\\ f'\left( {18.7} \right) = \mathop {\lim }\limits_{t \to 18.7} \frac{{\left[ {5t} \right] - \left[ {5\left( {18.7} \right)} \right]}}{{t - 18.7}}\\ f'\left( {18.7} \right) = \mathop {\lim }\limits_{t \to 18.7} \frac{{5t - 5\left( {18.7} \right)}}{{t - 18.7}}\\ f'\left( {18.7} \right) = \mathop {\lim }\limits_{t \to 18.7} \frac{{5\left( {t - 18.7} \right)}}{{t - 18.7}}\\ f'\left( {18.7} \right) = \mathop {\lim }\limits_{t \to 18.7} 5\\ f'\left( {18.7} \right) = 5 \end{array}$ Solución 2. Utilizando la definición de Newton $\begin{array}{l} f'\left( a \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {a + h} \right) - f\left( a \right)}}{h}\\ f'\left( {18.7} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {18.7 + h} \right) - f\left( {18.7} \right)}}{h}\\ f'\left( {18.7} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{\left[ {5\left( {18.7 + h} \right)} \right] - \left[ {5\left( {18.7} \right)} \right]}}{h}\\ f'\left( {18.7} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{\left[ {93.5 + 5h} \right] - \left[ {93.5} \right]}}{h}\\ f'\left( {18.7} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{5h}}{h}\\ f'\left( {18.7} \right) = \mathop {\lim }\limits_{h \to 0} 5\\ f'\left( {18.7} \right) = 5 \end{array}$ Como pudiste observar, la derivada de la función es $f'\left( {18.7} \right) = 5$. En este ejemplo, la derivada de la función de desplazamiento determina la razón de cambio instantánea de la posición respecto al tiempo; es decir, hemos calculado la velocidad instantánea ${v_i}$ en ${t_0} = 18.7$ segundos; es decir, ${v_i}(18.7) = f'\left( {18.7} \right) = 5\frac{m}{s}$.
-
Derivada de una función cuadrática
Ejemplo 3. La imagen muestra un objeto en caída libre cuya función de posición es $f\left( t \right) = - 5{t^2} + 20$, donde $t$ es la variable independiente y representa el tiempo; el desplazamiento se expresa en metros y el tiempo en segundos, que toma valores de 0 a 2 segundos. Cabe mencionar que este problema se retoma del objeto de aprendizaje «Concepto de la derivada de una función».
A continuación, determinaremos la derivada de la función cuadrática en el instante ${t_0} = a = 1.2$ segundos, utilizando las definiciones de Fermat y de Newton.
Solución 1. Utilizando la definición de Fermat $\begin{array}{l} f'\left( a \right) = \mathop {\lim }\limits_{t \to a} \frac{{f\left( t \right) - f(a)}}{{t - a}}\\ f'\left( {1.2} \right) = \mathop {\lim }\limits_{t \to 1.2} \frac{{\left[ { - 5{t^2} + 20} \right] - \left[ { - 5{{\left( {1.2} \right)}^2} + 20} \right]}}{{t - 1.2}}\\ f'\left( {1.2} \right) = \mathop {\lim }\limits_{t \to 1.2} \frac{{ - 5{t^2} + 20 + 5{{\left( {1.2} \right)}^2} - 20}}{{t - 1.2}}\\ f'\left( {1.2} \right) = \mathop {\lim }\limits_{t \to 1.2} \frac{{ - 5\left( {{t^2} - {{\left( {1.2} \right)}^2}} \right)}}{{t - 1.2}}\\ f'\left( {1.2} \right) = \mathop {\lim }\limits_{t \to 1.2} \frac{{ - 5\left( {t - 1.2} \right)\left( {t + 1.2} \right)}}{{t - 1.2}}\\ f'\left( {1.2} \right) = \mathop {\lim }\limits_{t \to 1.2} - 5\left( {t + 1.2} \right)\\ f'\left( {1.2} \right) = - 5\left( {1.2 + 1.2} \right)\\ f'\left( {1.2} \right) = - 12 \end{array}$ Solución 2. Utilizando la definición de Newton $\begin{array}{l} f'\left( a \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {a + h} \right) - f\left( a \right)}}{h}\\ f'\left( {1.2} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{\left[ { - 5{{\left( {1.2 + h} \right)}^2} + 20} \right] - \left[ { - 5{{\left( {1.2} \right)}^2} + 20} \right]}}{h}\\ f'\left( {1.2} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{\left[ { - 5\left( {{{\left( {1.2} \right)}^2} + 2\left( {1.2} \right)h + {h^2}} \right) + 20} \right] - \left[ { - 5{{\left( {1.2} \right)}^2} + 20} \right]}}{h}\\ f'\left( {1.2} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{ - 5{{\left( {1.2} \right)}^2} - 10\left( {1.2} \right)h - 5{h^2} + 20 + 5{{\left( {1.2} \right)}^2} - 20}}{h}\\ f'\left( {1.2} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{ - 12h - 5{h^2}}}{h} = \mathop {\lim }\limits_{h \to 0} \frac{{h\left( { - 12 - 5h} \right)}}{h}\\ f'\left( {1.2} \right) = \mathop {\lim }\limits_{h \to 0} \left( { - 12 - 5h} \right)\\ f'\left( {1.2} \right) = - 12 - 5\left( 0 \right)\\ f'\left( {1.2} \right) = - 12 \end{array}$ Como pudiste observar, la derivada de la función es $f'\left( {1.2} \right) = - 12$; el signo negativo indica que el objeto está cayendo. En este ejemplo, la derivada de la función determina la razón de cambio instantánea de la posición respecto al tiempo; es decir, hemos calculado la velocidad instantánea (${v_i}$) en ${t_0} = 1.2$ segundos.
${v_i}(1.2) = f'\left( {1.2} \right) = - 12\frac{m}{s}$
El siguiente recurso Geogebra te permite determinar la velocidad instantánea en diferentes instantes de tiempo. Observa que para la función cuadrática se tiene que la velocidad instantánea varía con el tiempo.
-
Derivada de una función cúbica
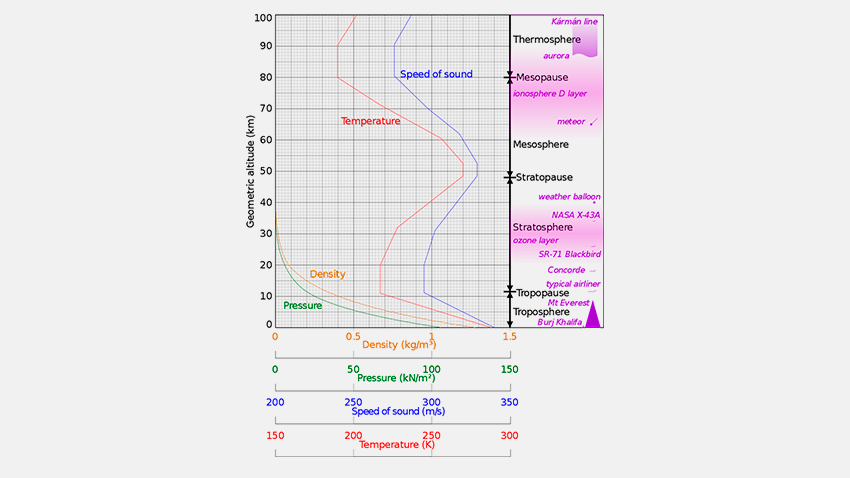
Ejemplo 4. En la imagen se muestran diversas características representativas de la atmósfera en función de la altura; una de ellas es la densidad atmosférica; dicha densidad (kg/m3) puede representarse con la función $f\left( x \right) = 1.25 - Ax + B{x^2} - C{x^3}$ donde x es la variable independiente que representa a la altura (en km) en el intervalo $0 \le x \le 30,000$; y $A = 1.096 \times {10^{ - 4}}$, $B = 3.42 \times {10^{ - 9}}$, $C = 3.6 \times {10^{ - 14}}$.
A continuación, determinaremos la derivada de la función cúbica en la altura ${x_0} = a = 10,000$km, utilizando las definiciones de Fermat y de Newton.
Solución 1. Utilizando la definición de Fermat $\begin{array}{l} f'\left( a \right) = \mathop {\lim }\limits_{x \to a} \frac{{f\left( x \right) - f(a)}}{{x - a}}\\ f'\left( {10,000} \right) = \mathop {\lim }\limits_{x \to 10,000} \frac{{f\left( x \right) - f(10,000)}}{{x - 10,000}}\\ f'\left( {10,000} \right) = \mathop {\lim }\limits_{x \to 10,000} \frac{{\left[ {1.25 - Ax + B{x^2} - C{x^3}} \right] - \left[ {1.25 - A\left( {10,000} \right) + B{{\left( {10,000} \right)}^2} - C{{\left( {10,000} \right)}^3}} \right]}}{{x - 10,000}}\\ f'\left( {10,000} \right) = \mathop {\lim }\limits_{x \to 10,000} \frac{{1.25 - Ax + B{x^2} - c{x^3} - 1.25 + A\left( {10,000} \right) - B{{\left( {10,000} \right)}^2} + C{{\left( {10,000} \right)}^3}}}{{x - 10,000}}\\ f'\left( {10,000} \right) = \mathop {\lim }\limits_{x \to 10,000} \frac{{ - Ax + A\left( {10,000} \right) + B{x^2} - B{{\left( {10,000} \right)}^2} - C{x^3} + C{{\left( {10,000} \right)}^3}}}{{x - 10,000}}\\ f'\left( {10,000} \right) = \mathop {\lim }\limits_{x \to 10,000} \frac{{ - A\left( {x - 10,000} \right) + B\left[ {{x^2} - {{\left( {10,000} \right)}^2}} \right] - C\left[ {{x^3} - {{\left( {10,000} \right)}^3}} \right]}}{{x - 10,000}}\\ f'\left( {10,000} \right) = \mathop {\lim }\limits_{x \to 10,000} \frac{{ - A\left( {x - 10,000} \right) + B\left( {x - 10,000} \right)\left( {x + 10,000} \right) - C\left( {x - 10,000} \right)\left[ {{x^2} + 10,000x + {{\left( {10,000} \right)}^2}} \right]}}{{x - 10,000}}\\ f'\left( {10,000} \right) = \mathop {\lim }\limits_{x \to 10,000} \frac{{\left( {x - 10,000} \right)\left\{ { - A + B\left( {x + 10,000} \right) - C\left[ {{x^2} + 10,000x + {{\left( {10,000} \right)}^2}} \right]} \right\}}}{{x - 10,000}}\\ f'\left( {10,000} \right) = \mathop {\lim }\limits_{x \to 10,000} - A + B\left( {x + 10,000} \right) - C\left[ {{x^2} + 10,000x + {{\left( {10,000} \right)}^2}} \right]\\ f'\left( {10,000} \right) = - A + B\left( {10,000 + 10,000} \right) - C\left[ {{{\left( {10,000} \right)}^2} + 10,000\left( {10,000} \right) + {{\left( {10,000} \right)}^2}} \right]\\ f'\left( {10,000} \right) = - A + 2B\left( {10,000} \right) - 3C{\left( {10,000} \right)^2} \end{array}$ Solución 2. Utilizando la definición de Newton $\begin{array}{l} f'\left( a \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {a + h} \right) - f\left( a \right)}}{h}\\ f'\left( {10,000} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {10,000 + h} \right) - f\left( {10,000} \right)}}{h}\\ f'\left( {10,000} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{\left[ {1.25 - A\left( {10,000 + h} \right) + B{{\left( {10,000 + h} \right)}^2} - C{{\left( {10,000 + h} \right)}^3}} \right] - \left[ {1.25 - A\left( {10,000} \right) + B{{\left( {10,000} \right)}^2} - C{{\left( {10,000} \right)}^3}} \right]}}{h}\\ f'\left( {10,000} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{\left[ {1.25 - A\left( {10,000 + h} \right) + B\left( {10,{{000}^2} + 2\left( {10,000} \right)h + {h^2}} \right) - C\left( {10,{{000}^3} + 3{{\left( {10,000} \right)}^2}h + 3\left( {10,000} \right){h^2} + {h^3}} \right)} \right] - \left[ {1.25 - A\left( {10,000} \right) + B{{\left( {10,000} \right)}^2} - C{{\left( {10,000} \right)}^3}} \right]}}{h}\\ f'\left( {10,000} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{\left[ {1.25 - A\left( {10,000} \right) - Ah + B\left( {10,{{000}^2}} \right) + 2\left( {10,000} \right)Bh + B{h^2} - C\left( {10,{{000}^3}} \right) - 3{{\left( {10,000} \right)}^2}Ch - 3C\left( {10,000} \right){h^2} - C{h^3}} \right] - \left[ {1.25 - A\left( {10,000} \right) + B{{\left( {10,000} \right)}^2} - C{{\left( {10,000} \right)}^3}} \right]}}{h}\\ f'\left( {10,000} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{ - Ah + 2\left( {10,000} \right)Bh + B{h^2} - 3{{\left( {10,000} \right)}^2}Ch - 3C\left( {10,000} \right){h^2} - C{h^3}}}{h}\\ f'\left( {10,000} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{h\left[ { - A + 2\left( {10,000} \right)B - 3{{\left( {10,000} \right)}^2}C + Bh - 3C\left( {10,000} \right)h - C{h^2}} \right]}}{h}\\ f'\left( {10,000} \right) = \mathop {\lim }\limits_{h \to 0} \left[ { - A + 2\left( {10,000} \right)B - 3{{\left( {10,000} \right)}^2}C + Bh - 3C\left( {10,000} \right)h - C{h^2}} \right]\\ f'\left( {10,000} \right) = - A + 2B\left( {10,000} \right) - 3C{\left( {10,000} \right)^2} \end{array}$ Como pudiste observar, la derivada de la función es $f'\left( {10,000} \right) = - A + 2B\left( {10,000} \right) - 3C{\left( {10,000} \right)^2}$. En este ejemplo, la derivada determina la razón de cambio instantánea de la densidad respecto a la altura, para la altura indicada.
Utilizando los cocientes de Newton y de Fermat, determina la derivada de la función $f\left( x \right) = 2x + 3$ para ${x_0} = 2$. Indica el resultado en el recuadro.
De una hoja de lámina cuadrada de 20 cm de lado se quiere fabricar una caja de base cuadrada sin tapa, cortando cuadrados en las esquinas de igual tamaño para doblar las cejas y formar las caras laterales. En el objeto de aprendizaje “Variación y razón de cambio de una función ”, se determinó que el volumen de una caja, cuando se cortan cuadrados en las esquinas de lado x, está determinado por la función $v\left( x \right) = 4{x^3} - 80{x^2} + 400x$.
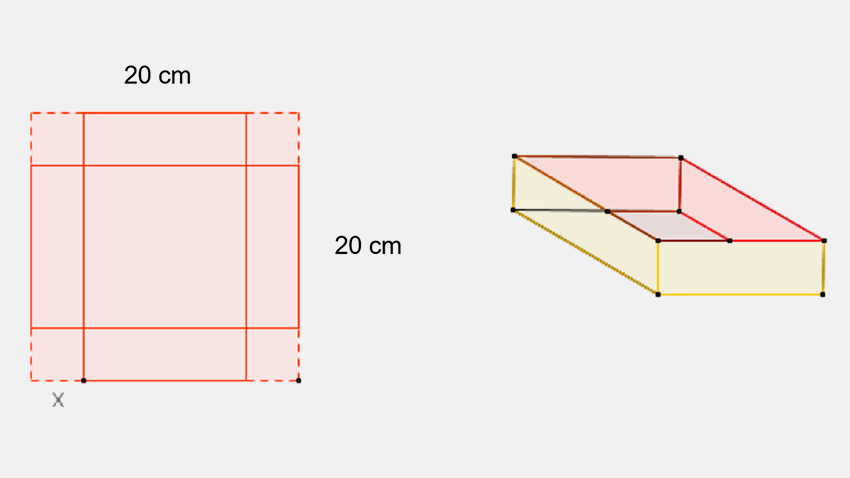
Utilizando los cocientes de Newton y de Fermat, determina la derivada de la función para ${x_0} = 2$. Indica el resultado en el recuadro.