En la siguiente imagen se muestran los puntos $A , B$ y $C$ localizados en tres ubicaciones distintas en Ciudad Universitaria de la UNAM; tales puntos están localizados en el Estadio Olímpico Universitario, en la Escuela Nacional de Trabajo Social y en Instituto de Física. Observa que se forma el triángulo $\bigtriangleup ABC$.
Si se desea colocar un módulo de BiciPUMA en un lugar equidistante a las tres ubicaciones antes mencionadas, ¿sabes dónde se localizaría?
Si se desea colocar un módulo de BiciPUMA en un lugar equidistante a las tres ubicaciones antes mencionadas, ¿sabes dónde se localizaría?

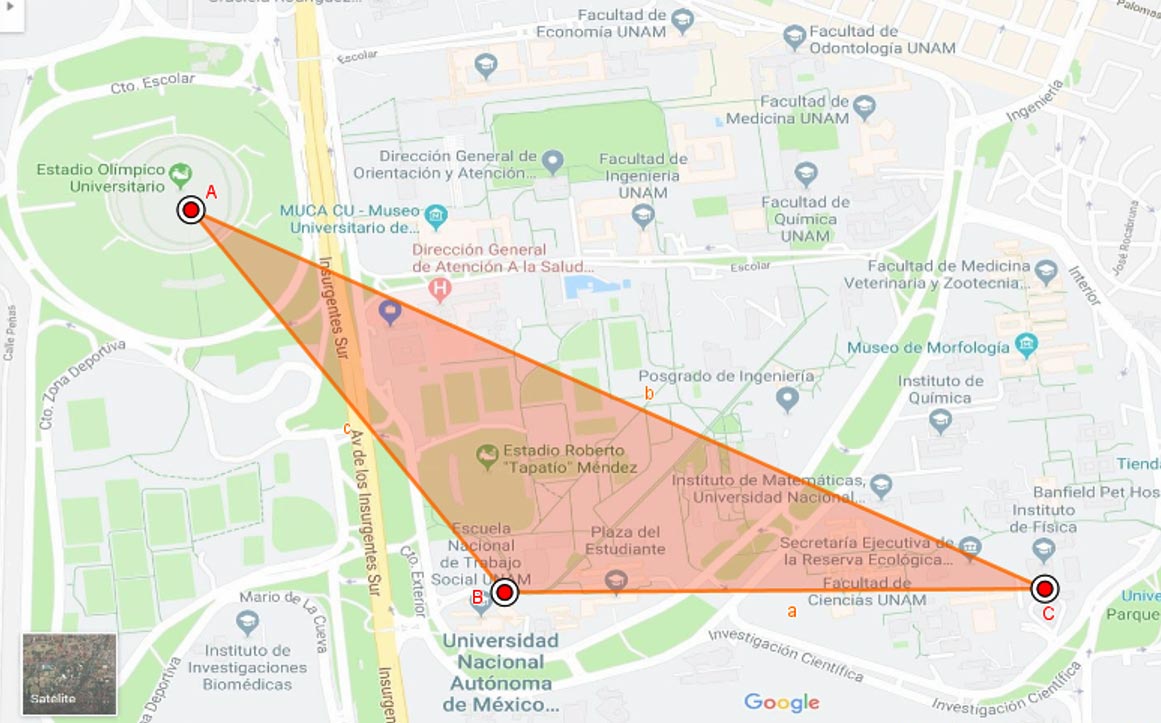

En el siguiente recurso GeoGebra se muestra el punto $D$ (llamado circuncentro), equidistante a los puntos $A , B$ y $C$, donde se colocaría el módulo de BiciPUMA ¿Observaste en qué Facultad se localizaría el módulo?
El punto D es un punto notable del triángulo conocido como circuncentro; que es la intersección de tres rectas notables del triángulo conocidas como mediatrices. En el recurso GeoGebra pudiste observar que el circuncentro equidista de los tres vértices del triángulo.
Además del circuncentro y la mediatrices, en esta sección estudiarás los puntos y rectas notables más conocidos del triángulo. Dichos elementos se indican en la siguiente tabla:
| Rectas notables | Puntos notables |
|---|---|
| Alturas | Ortocentro |
| Medianas | Baricentro |
| Mediatrices | Circuncentro |
| Bisectrices | Incentro |
Para que conozcas más al respecto te pedimos des clic en las siguientes pestañas para que revises la explicación:
Altura: Es el segmento perpendicular a un lado o su prolongación y que pasa por el vértice opuesto.
Todo triángulo tiene tres alturas, las cuales son concurrentes; el punto de intersección de las alturas se conoce como ortocentro.

Con el recurso GeoGebra construye triángulos diferentes desplazando los vértices $A, B$ y $C$; Haz clic en las casillas del lado derecho para mostrar las tres alturas del triángulo.
Mediana: Es un segmento que va de un vértice al punto medio del lado opuesto.
Todo triángulo tiene tres medianas, las cuales son concurrentes. El punto de concurrencia de las medianas se conoce como baricentro.

Con el siguiente GeoGebra construye triángulos diferentes desplazando los vértices $A, B$ y $C$; Haz clic en las casillas del lado derecho para mostrar las tres medianas del triángulo. Observa que las medianas se intersecan en un único punto llamado baricentro.
En la siguiente figura se muestra un terreno triangular de $94,373.293m$2. El propietario quiere dividirlo en seis partes iguales, ¿sabes cómo podría hacerlo?
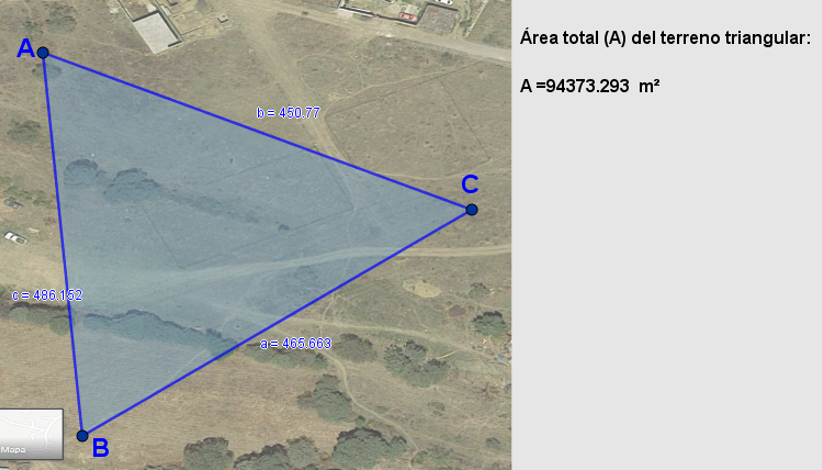

En el recurso GeoGebra observarás la solución al planteamiento propuesto. Haz clic en la casilla “Mostrar medianas” y observa que las medianas dividen al triángulo ΔABC en seis triángulos pequeños de igual área. Desplaza los vértices para generar triángulos diferentes.
A continuación, se indican dos propiedades importantes relacionadas con la mediana y el baricentro.
Propiedades
- Las medianas dividen el triángulo en seis triángulos de igual área.
- El baricentro divide cada mediana en dos segmentos donde la distancia del baricentro al vértice es el doble de la distancia del baricentro al punto medio del lado opuesto. Dicho de otra manera, el baricentro se encuentra a las dos terceras partes de cada vértice del triángulo.

La segunda propiedad puedes verificarla mediante el siguiente recurso GeoGebra . Construye triángulos diferentes desplazando los vértices $A, B$ y $C$; Haz clic en las casillas del lado derecho para mostrar las tres medianas del triángulo. Observa las distancias del baricentro a los vértices y compáralas con las distancias del baricentro a los puntos medios de los lados. Observa que el baricentro se encuentra a las dos terceras partes de cada vértice del triángulo.
Mediatriz: Es la recta perpendicular trazada en el punto medio de cada lado de un triángulo.
Los triángulos tienen tres mediatrices que son concurrentes. El punto de concurrencia de las tres mediatrices es el circuncentro.

Con el recurso GeoGebra construye triángulos diferentes desplazando los vértices $A,B$ y $C$; haz clic en las casillas del lado derecho para mostrar las tres mediatrices del triángulo.
Si se trazan segmentos del circuncentro a los vértices del triángulo, observarás que dichos segmentos tienen una característica en común ¿Sabes cuál es dicha característica?

Con el recurso GeoGebra construye triángulos diferentes desplazando los vértices $A,B$ y $C$; Haz clic en las casillas del lado derecho para mostrar las tres mediatrices del triángulo. Observa con atención los tres segmentos que van del circuncentro a los vértices y observa la característica que tienen en común.
Escribe las respuestas correctas.

Con el recurso GeoGebra construye triángulos diferentes desplazando los vértices $A,B$ y $C$; Haz clic en las casillas del lado derecho para mostrar las tres mediatrices del triángulo. Observa que la circunferencia circunscrita siempre pasa por los vértices del triángulo.
Bisectriz: Es la semirrecta que divide un ángulo del triángulo en dos ángulos congruentes. Se extiende desde el vértice del ángulo hasta su lado opuesto.
Las tres bisectrices de un triángulo son concurrentes. El punto de concurrencia para las bisectrices es el incentro.

Con el recurso GeoGebra construye triángulos diferentes desplazando los vértices $A,B$ y $C$; Haz clic en las casillas del lado derecho para mostrar las tres bisectrices del triángulo.

Con el recurso GeoGebra construye triángulos diferentes desplazando los vértices $A,B$ y $C$. Observa con atención los tres segmentos perpendiculares a las bases que pasan por el incentro y observa la característica que tienen en común.
Escribe las respuestas correctas.

Analiza la circunferencia inscrita en el siguiente recurso GeoGebra . Observa que el incentro es el centro de la circunferencia inscrita en el triángulo, la cual es tangente a los tres lados del triángulo. Observa que el incentro equidista de los puntos de intersección entre la circunferencia inscrita y los lados del triángulo.
En las secciones anteriores aprendiste que el triángulo tiene cuatro puntos notables: ortocentro, baricentro, circuncentro e incentro. En el siguiente recurso GeoGebra observarás que tres puntos notables son colineales, ¿sabes cuáles son? A la recta que forman los puntos notables colineales se le conoce como Recta de Euler.

Con el recurso GeoGebra construye triángulos diferentes desplazando los vértices $A, B$ y $C$; haz clic en las casillas del lado derecho para mostrar las rectas y puntos notables del triángulo. Observa cuáles puntos notables son colineales.
Selecciona la opción correcta. A partir de lo que observaste en el recurso interactivo anterior se puede afirmar que:
| La recta de Euler está formada por los siguientes puntos notables |
|---|
El ortocentro, el circuncentro y el baricentro de todo triángulo son colineales y determinan a la recta de Euler.
La recta de Euler es una recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo.


