En este apartado se presentan actividades y problemas de corte geométrico para que los resuelvas y consolides los aprendizajes que lograste sobre las propiedades, desigualdad y la clasificación del triángulo, así como sus rectas y puntos notables.
1. Selecciona la opción correcta; arrastra las opciones de los recuadros en verde al lugar adecuado.
Recuerda que los triángulos se clasifican con base en dos criterios: 1) por la medida de sus lados y 2) por la medida de sus ángulos.
Los triángulos clasificados por la medida de sus lados son:
- Triángulo equilátero. Tiene tres lados iguales.
- Triángulo isósceles. Tiene dos lados iguales.
- Triángulo escaleno. Tiene tres lados diferentes.
Los triángulos clasificados por la medida de sus ángulos son:
- Triángulo acutángulo. Tiene todos los ángulos agudos.
- Triángulo obtusángulo. Tiene un ángulo obtuso.
- Triángulo rectángulo. Tiene un ángulo recto.
- Triángulo equiángulo. Tiene todos los ángulos iguales
2. Indica el tipo de triángulo para cada una de las siguientes figuras, considerando los criterios basados en la medida de los lados y de los ángulos. Escribe en los recuadros la respuesta correcta.
4. En el triángulo $\bigtriangleup ABC$ las medidas de sus ángulos son $\angle A = 50 ^o$ y $\angle B = 36 ^o$. Determina el valor de $\angle C$ e indica que tipo de triángulo es $\bigtriangleup ABC$.
5. Determina el valor de $x$, así como los valores de los ángulos exteriores $\angle \alpha$, $\angle \beta$ y $\angle \gamma$, considerando que:
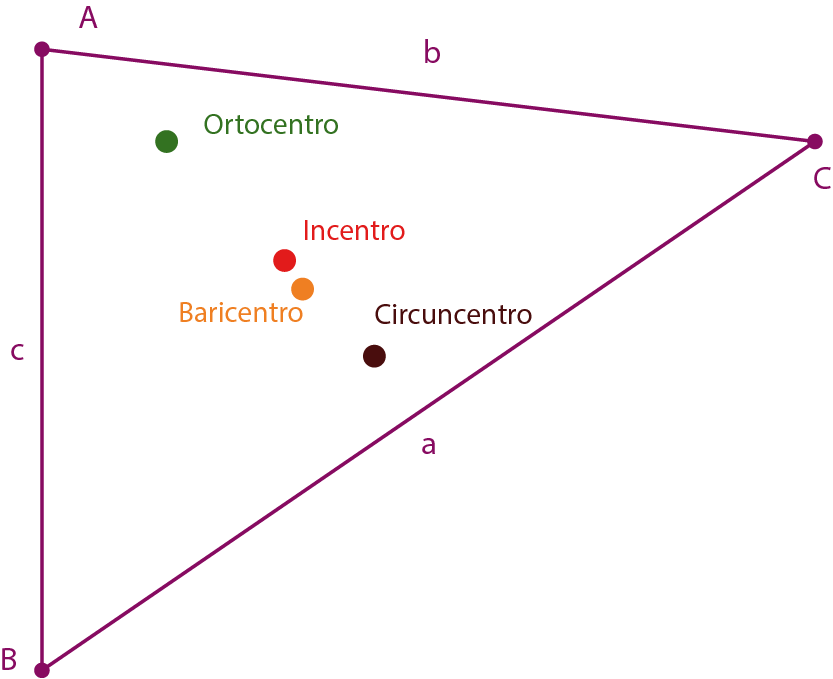
6. Completa la siguiente oración con las respuestas correctas referentes a las rectas y puntos notables, indicando el nombre del punto D (en rojo) y de las rectas de color naranja.
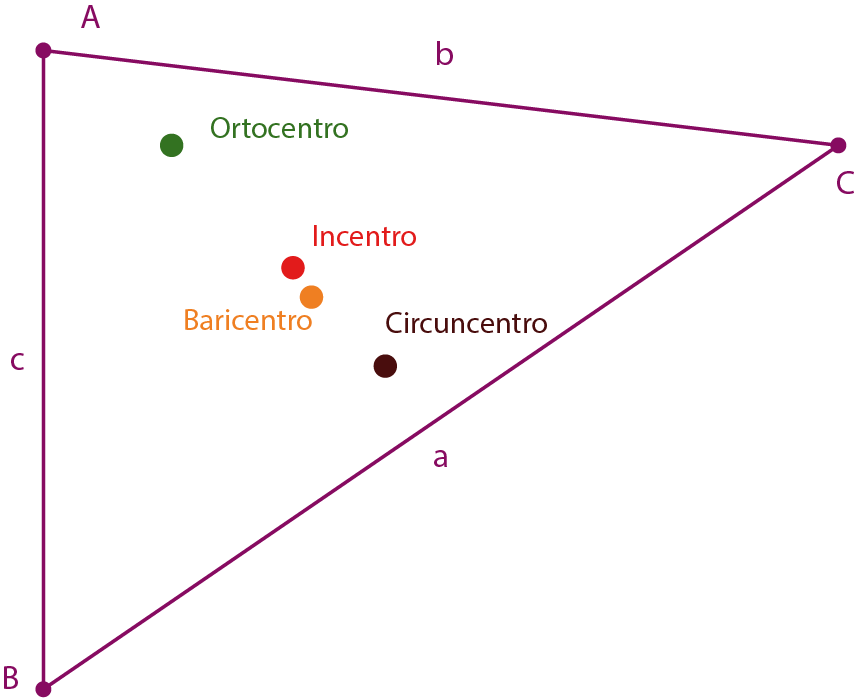
7. La recta de Euler está conformada por:
-
- ortocentro
- incentro
- circuncentro
- circuncentro
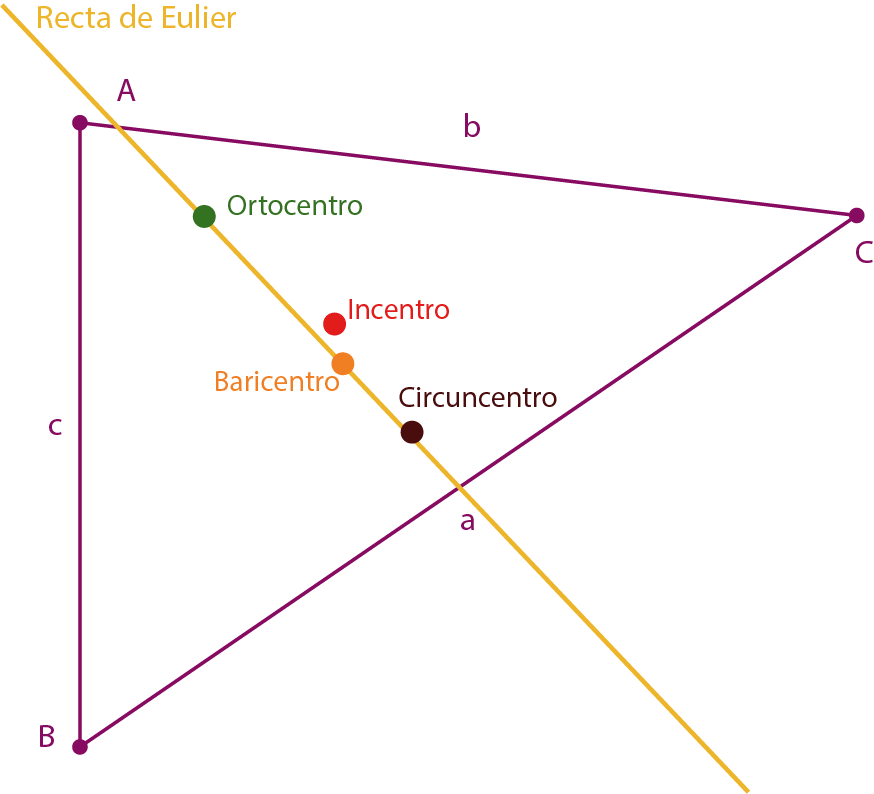
Recuerda que la recta de Euler es una recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo.
-
- ortocentro
- incentro
- circuncentro
- circuncentro
Recuerda que el incentro es el centro de una circunferencia, llamada circunferencia inscrita, que es tangente a los lados del triángulo.
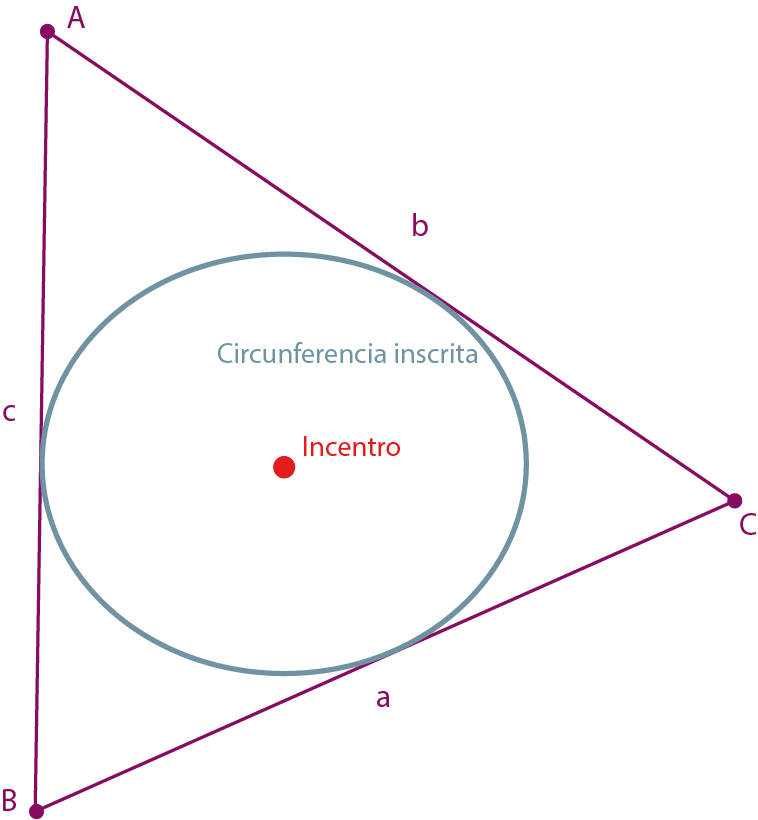
8. Para construir una circunferencia inscrita al triángulo se debe considerar el
9. En el triángulo ∆ABC se muestran las medianas y el baricentro G. Determina la longitud de los segmentos GN, CG y GM, considerando que AG=227.36, GB=195.04 y GL=112.74.
Escribe las respuestas correctas.
10.Una empresa de telecomunicaciones desea colocar una antena para tener cobertura en la región delimitada por el triángulo ΔABC, tal como la que se muestra en la imagen.
Si se sabe que el punto D corresponde al circuncentro del triángulo y que la distancia entre las localidades C y D es CD = 35.1 km. ¿Cuáles son las distancias AD y BD?
Escribe las respuestas correctas.


