A continuación práctica el contenido revisado y resuelve los siguientes problemas.
1. En el triángulo $\bigtriangleup ABC$ las medidas de sus ángulos son $\angle A = 50 ^o$ y $\angle B = 36 ^o$. A continuación, se determinará el valor de $\angle C$. Después de conocer el valor del ángulo $\angle C$, indica que tipo de triángulo es $\bigtriangleup ABC$.

Solución:
Se sabe que para todo triángulo la suma de sus ángulos interiores es $180 ^o$ . Por lo tanto, para el $\bigtriangleup ABC$ se tiene que $\angle A + \angle B + \angle C = 180 ^o$, por tanto
$50 ^o + 36 ^o + \angle C = 180 ^o$
Al despejar $\angle C$ de la ecuación anterior se tiene que
$\angle C = 94 ^o$
2. Para el triángulo $\bigtriangleup DEF$, $\angle D$ es un ángulo recto y $\angle E = 46 ^o$. Determina el valor del ángulo $\angle F$.
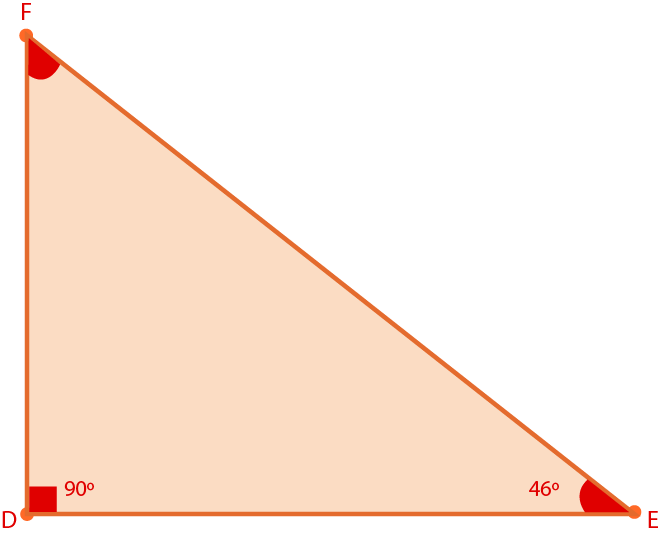
Escribe la respuesta correcta.
3. Determina los valores de los ángulos $\angle \alpha$, $\angle J$, $\angle K$ y $\angle L$, considerando que
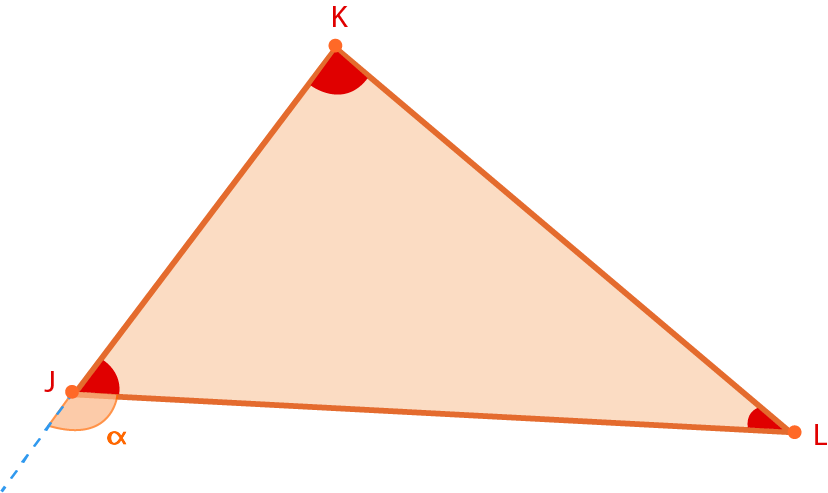
Solución:
Dado que la suma de dos ángulos interiores es igual al ángulo exterior no adyacente, entonces,
A partir del valor de $x=10$ es posible determinar los valores de los ángulos $\angle \alpha$, $\angle K$ y $\angle L$, sustituyendo en las ecuaciones correspondientes.
El valor de $\angle J$ se determina utilizando la propiedad de la suma de los ángulos interiores.
Determina el valor del ángulo $\angle J$.
4. En el triángulo $\bigtriangleup PQR$ las medidas de sus ángulos son $\angle P = 4x$, $\angle Q = 5x$ y $\angle R= 6x$ Determina el valor de $x$ , así como $\angle P$, $\angle Q$ y $\angle R$.


