El estudio de los triángulos se remonta a más de 3000 años a.C. Los babilonios y los egipcios utilizaron las medidas de los triángulos en la agricultura, en la construcción de pirámides y en la astronomía. La tablilla Plimpton 322, que data del periodo babilónico antiguo (1900 a.C. a 1600 a.C), guarda testimonio de las ideas babilónicas relacionadas con la medición de los triángulos.
Con el desarrollo de la geometría, el estudio de los triángulos tuvo un mayor apogeo en la Grecia Clásica, especialmente con los trabajos de Thales de Mileto, Pitágoras y Euclides. Por ejemplo, hace más de 2,500 años, los griegos calculaban el área de cualquier polígono al dividirlo en triángulos y sumar el área de dichos triángulos; con esta idea, incluso, podían calcular el área de cualquier figura curveada mediante el llamado “método de agotamiento”, que consistía en inscribir y circunscribir polígonos en la figura. El método de agotamiento permite tener una mejor aproximación al valor exacto del área conforme se incremente el número de lados de los polígonos.
Tablilla Plimpton 322
Por ejemplo, en la siguiente figura se muestra una circunferencia de radio $R=1.1 cm$ (en color rojo); también se muestra un polígono inscrito y uno circunscrito. Las áreas de los polígonos inscrito y del circunscrito, $A_{PI}$ (en color azul) y $A_{PC}$ (en color verde) respectivamente, son $A_{PI} = 2.877 {cm^2}$ y $A_{PC} = 4.396 {cm^2}$.
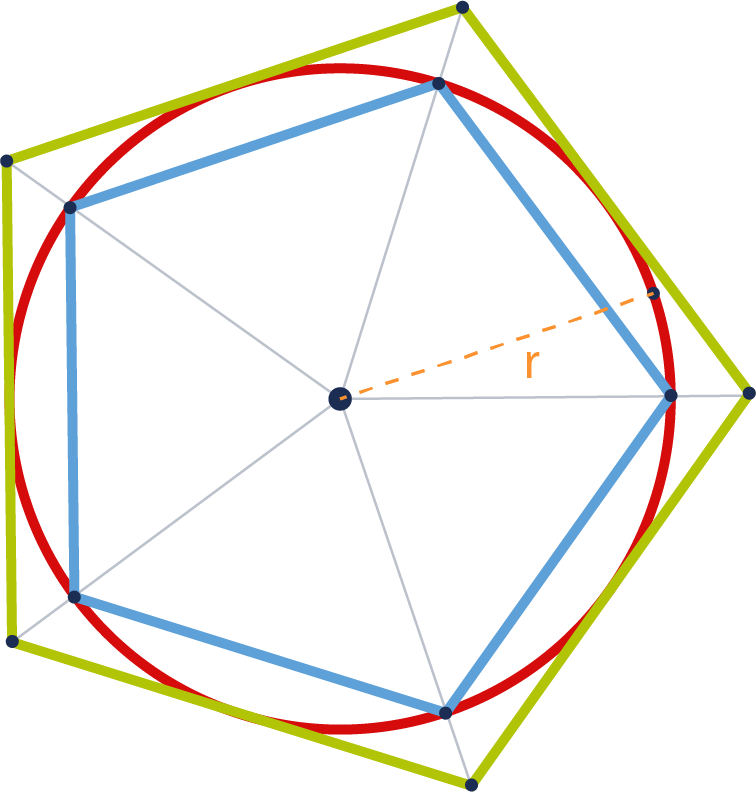
El “método de agotamiento” afirma que el área del circulo $({A_C})$ se encuentra entre los valores de $A_{PI}$ y $A_{PC}$:
$${A_{PI}} \le {A_C} \le {A_{PC}}$$Es decir:
$$2.877\;{cm^2} \le {A_C}\; \le 4.396\;{cm^2}$$Si se incrementa el número de lados de los polígonos entonces las áreas de éstos tendrán una mejor aproximación al área de la circunferencia. Por ejemplo, si se tienen polígonos de 50 lados, las áreas de los polígonos son $A_{PI} = 3.791 {cm^2}$ y $A_{PC} = 3.806 {cm^2}$. Entonces el área del círculo $({A_C})$ se encuentra entre tales valores, es decir
$$3.791\;{cm^2} \le {A_C}\; \le 3.806\;{cm^2}$$Observa que conforme se incrementa el número de lados de los polígonos, las áreas $A_{PI}$ y $A_{PC}$ se aproximan al área del círculo ${A_C}$, cuyo valor exacto se obtiene mediante la fórmula ${A_C} = \pi \times {r^2}$, es decir, ${A_C} = \pi \times {\left( {1.1} \right)^2} \approx 3.801{cm^2}$.

En el recurso Geogebra se ilustra el método de agotamiento para calcular el área de un círculo de radio $r = 1.1 cm$. Para calcular el área del círculo $({A_C})$ se han inscrito y circunscrito dos polígonos; ${A_C}$ se estima a partir de las áreas de los polígonos inscrito y circunscrito, $A_{PI}$ y $A_{PC}$ respectivamente. Observa que conforme se incrementa el número de lados de los polígonos, los valores de $A_{PI}$ y $A_{PC}$ proporcionan una mejor aproximación al valor exacto del área del círculo.
Desplaza el deslizador para modificar el número de lados de los polígonos inscrito y circunscrito; observa que conforme se incrementa el número de lados, las áreas $A_{PI}$ y $A_{PC}$ se aproximan al valor real del área del círculo.
En el recurso GeoGebra observaste que el antiguo método de agotamiento permite estimar el área de una circunferencia por medio de polígonos y triángulos. En la actualidad, el uso y estudio de los triángulos aún es vigente. Por ejemplo, se emplean vigas trianguladas (llamadas vigas reticuladas o arriostradas) para la construcción de estructuras y grandes edificaciones; estas vigas están formadas por triángulos unidos entre sí. Las vigas reticuladas poseen alta resistencia a la compresión ya que, debido a sus secciones triangulares, no se deforman cuando actúa sobre ellas una fuerza. En las siguientes fotografías se muestran obras civiles compuestas de vigas reticuladas.

Con este material comprenderás los conceptos básicos de geometría del triángulo y sus relaciones geométricas, a través de algunos conceptos y recursos interactivos en GeoGebra, para aplicarlos en la resolución de problemas.


