¿Sabes qué tienen en común un triángulo equilátero, un isósceles, un rectángulo y un obtusángulo?
En las secciones anteriores aprendiste que existen diferentes tipos de triángulos y que tienen características particulares que los diferencian. En esta sección aprenderás que los triángulos tienen características que son comunes a todos los tipos de triángulos; a estas características comunes se les conoces como propiedades de los triángulos.
Las tres propiedades que se revisarán en esta sección están relacionadas con los ángulos interiores y exteriores y son:
Sin importar el tipo de triángulo, la suma de sus ángulos interiores tiene un valor constante ¿Sabes cuál es el valor de la suma de los ángulos interiores de un triángulo?
En el recurso Geogebra se muestran cuatro triángulos diferentes $ΔABC$, $ΔDEF$, $ΔGHI$ y $ΔJKL$ y se muestran sus ángulos interiores; en caso de ser necesario, mueve los vértices de los triángulos para construir triángulos diferentes.
Suma los ángulos interiores y anota los resultados en los cuadros amarillos; hazlo para cada triángulo. Pon atención en los resultados de la suma de los ángulos interiores de los diferentes triángulos.
Completa la siguiente oración. A partir de lo que observaste en el recurso interactivo anterior se puede afirmar que:
Los triángulos también tienen ángulos exteriores; para construir un ángulo exterior se prolonga un lado más allá del vértice, tal como se muestra en la figura ¿Sabes cuál es el valor de la suma de los ángulos exteriores?
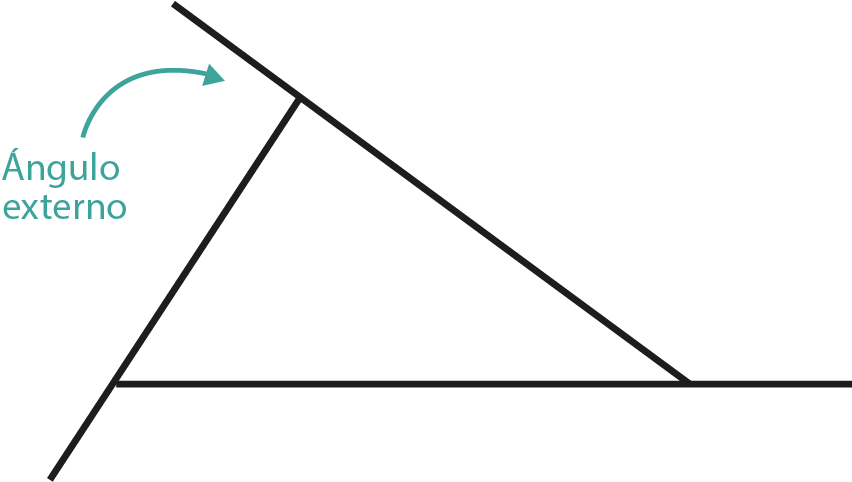
En el recurso Geogebra se muestran tres triángulos diferentes $ΔABC$, $ΔDEF$ y $ΔGHI$ y se muestran sus ángulos exteriores; en caso de ser necesario, mueve los vértices de los triángulos para construir triángulos diferentes.
Suma los ángulos exteriores y anota los resultados en los cuadros amarillos; hazlo para cada triángulo. Pon atención en los resultados de la suma de los ángulos exteriores de los diferentes triángulos.
Completa la siguiente oración. A partir de lo que observaste en el recurso interactivo anterior se puede afirmar que:
Ahora que sabes que la suma de los ángulos exteriores de todo triángulo es igual a 360°, revisa la siguiente demostración matemática elaborada en Geogebra .
Pon atención en el texto resaltado en color amarillo y observa la figura correspondiente; posteriormente, haz clic en el cuadro de verificación (izquierda), observa la nueva figura que se presenta y por atención en el texto que se resaltará nuevamente en color amarillo. Continúa haciendo clic en los cuadros de verificación que aparecerán según avances en la comprensión del material.
En la figura se muestran dos ángulos interiores y un ángulo exterior no adyacente ¿Sabes qué relación hay entre la suma de dos ángulos interiores con el ángulo exterior no adyacente?
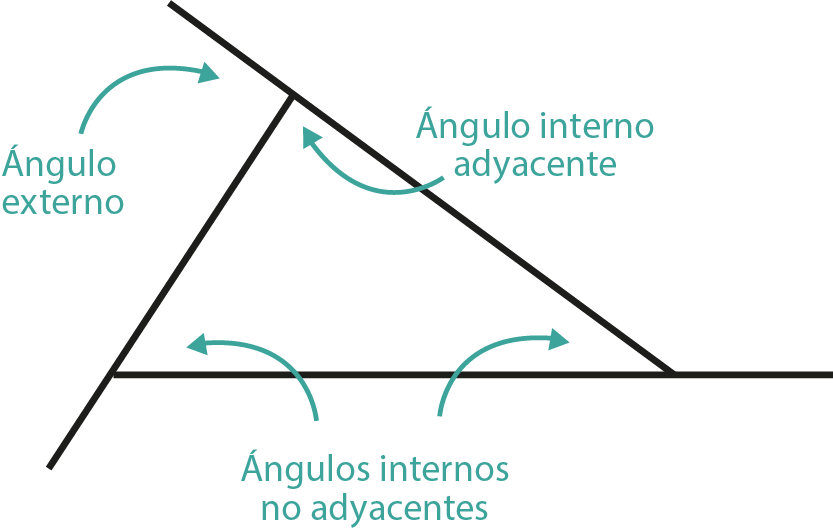
En el recurso Geogebra podrás ver tres triángulos diferentes $ΔABC$, $ΔDEF$ y $ΔGHI$ y se muestran dos ángulos interiores y un ángulo exterior no adyacente; en caso de ser necesario, mueve los vértices de los triángulos para construir triángulos diferentes.
Suma los dos ángulos interiores y anota los resultados en los cuadros amarillos; hazlo para cada triángulo. Compara el valor de la suma con el ángulo exterior no adyacente.
Selecciona la opción correcta. A partir de lo que observaste en el recurso interactivo anterior se puede afirmar que:
Un ángulo exterior de un triángulo es igual a la suma de los dos ángulos interiores no adyacentes.
Ahora que sabes que un ángulo exterior de un triángulo es igual a la suma de los dos ángulos interiores no adyacentes, revisa la siguiente demostración matemática elaborada en Geogebra.
Pon atención en el texto resaltado en color amarillo y observa la figura correspondiente; posteriormente, haz clic en el cuadro de verificación (izquierda), observa la nueva figura que se presenta y por atención en el texto que se resaltará nuevamente en color amarillo. Continúa haciendo clic en los cuadros de verificación que aparecerán según avances en la comprensión del material.