Un triángulo (símbolo $Δ$) es una porción del plano limitada por tres rectas que se cortan dos a dos en tres puntos.
Los puntos de intersección de las rectas son los vértices; y los segmentos de recta son los lados del triángulo; además, dos lados contiguos forman uno de los ángulos interiores del triángulo. En consecuencia, los triángulos tienen tres lados, tres vértices y tres ángulos interiores.
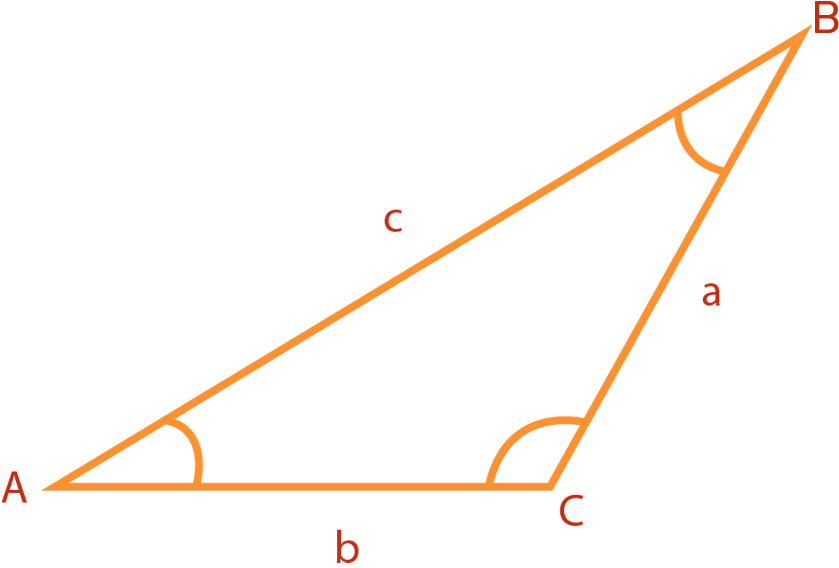
En la figura 1 se muestra la forma general de un triángulo (denominado como triángulo $ΔABC$), donde las letras $A$, $B$ y $C$ denotan a los ángulos internos y a los vértices; las letras minúsculas denotan a los lados del triángulo.
Generalmente, para nombrar a un lado se utiliza la letra minúscula correspondiente al vértice opuesto; es decir, el lado opuesto al vértice $A$ se designa con la letra $a$.
Clasificación de los triángulos
Los triángulos se clasifican con base en dos criterios: 1) por la medida de sus lados y 2) por la medida de sus ángulos. En los siguientes recursos GeoGebra analizarás cada una de estas clasificaciones.
Triángulos clasificados por la medida de sus lados
Una manera de clasificar a los triángulos es por la medida de sus lados, y para ello se considera el número de lados iguales o diferentes. En el siguiente recurso GeoGebra se muestran los tipos de triángulos existentes según la clasificación por la medida de sus lados; por ejemplo, observarás que un triángulo con tres lados iguales se conoce como triángulo equilátero ¿Sabes cómo se le llama al triángulo con dos lados iguales y cómo se le llama al triángulo con todos sus lados diferentes?

Revisa el recurso Geogebra . Haz clic en los puntos y desplázalos para generar triángulos diferentes; observa que los triángulos se clasifican según sean las medidas de sus lados.
Después de revisar la clasificación de los triángulos por la medida de sus lados, completa los siguientes enunciados:

Ya que has entendido la clasificación de los triángulos por la medida de los lados, revisa con atención el recurso Geogebra , e indica que tipo de triángulo es el que se presenta.
Triángulos clasificados por la medida de sus ángulos
Otra manera de clasificar a los triángulos es por la medida de sus ángulos. En el siguiente recurso GeoGebra se muestran los tipos de triángulos existentes según la clasificación por la medida de sus ángulos; por ejemplo, observarás que un triángulo con tres ángulos agudos se conoce como triángulo acutángulo ¿Sabes cómo se le llama al triángulo con un ángulo obtuso? ¿Y cómo se le conoce al triángulo con un ángulo recto? ¿Y al que tiene todos los ángulos iguales?

Revisa el recurso Geogebra y observa la clasificación de los triángulos con base en la medida de sus ángulos. Haz clic en los puntos y desplázalos para generar triángulos de diferentes medidas.
Después de revisar la clasificación de los triángulos por la medida de sus ángulos, completa los siguientes enunciados:

Ya que has entendido la clasificación de los triángulos por los criterios de la medida de los lados y la medida de los ángulos, revisa con atención el recurso Geogebra , e indica que tipo de triángulo es el que se presenta.
Después de revisar la clasificación de los triángulos por los criterios de los lados y de los ángulos, completa la siguiente oración, arrastrando las respuestas correctas:
Todo triángulo equilátero también es isósceles y equiángulo. Es isósceles porque cumple con la condición de tener dos lados iguales; es equiángulo porque cumple con la condición de tener todos los lados iguales, así como los ángulos interiores iguales.


