El estudio gráfico de la función de segundo grado, nos permite comprender la relación que existe entre sus diversas formas algebraicas y su representación en el plano cartesiano, con la finalidad de comprender las variaciones que se derivan de la modificación de los parámetros de la forma general $y=ax^2+bx+c$ y de la forma estándar $y=a(x-h)^2+k$ de la función cuadrática.
La intersección de la función con alguna recta horizontal, correspondiente a un valor del eje y (usualmente $y=0$), define una ecuación de segundo grado donde las raíces se interpretan como “ceros de la función”.
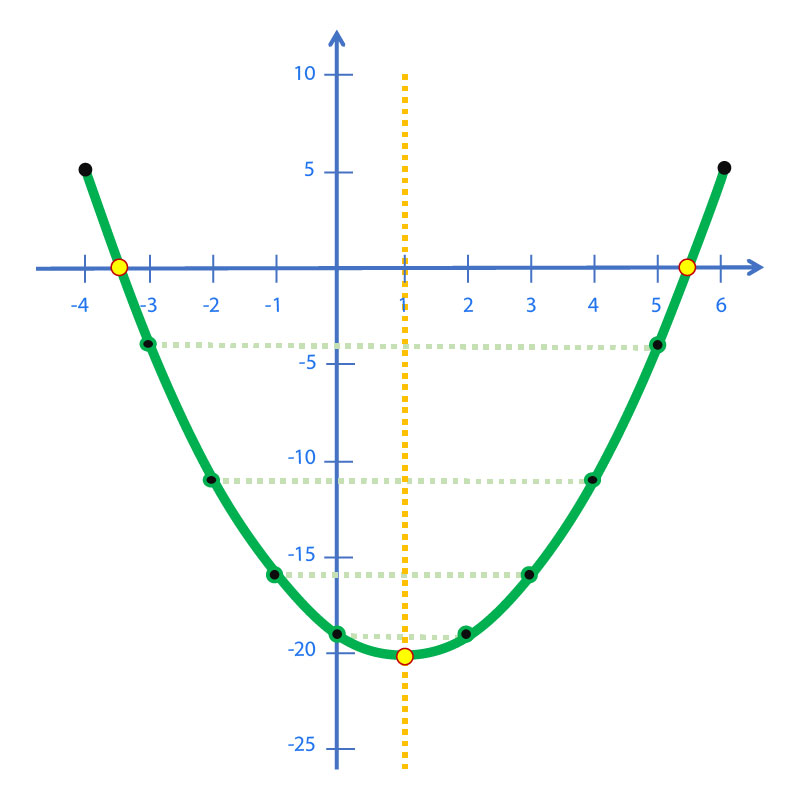
La gráfica de la función de segundo grado toma el nombre de parábola, la cual es una figura geométrica simétrica, con una concavidad o dirección de apertura, la cual definirá un valor máximo o mínimo de la función. Estos parámetros pueden observarse para bosquejar rápidamente la gráfica de la función o bien, el proceso inverso, a partir de una gráfica obtener la expresión algebraica de la misma.
Alcanzar de manera intuitiva este aprendizaje y asociarlo con la rapidez de cambio de la función es una habilidad particular que debe adquirir el estudiante para lograr un aprendizaje significativo y aplicarlo en la solución de problemas.
Con este material analizarás el comportamiento de las funciones cuadráticas en términos de sus parámetros mediante el contraste de la representación gráfica y analítica, para establecer las diferencias de este tipo de variación con la lineal.


