Actividad final - Estudio de la función cuadrática

Con esta actividad podrás verificar el aprendizaje del análisis algebráico y gráfico de la función de segundo grado.

Parte 1 Parte 2 Parte 3

Gráficas

Escribe el número de las gráficas en los espacios correspondientes y completa la tabla con la información que falta.

1	2	3	4

Gráfica	Ecuación	$a$	Concavidad	$V$
$4$	$y={\frac{1}{2}(x-3)^2+4}$	$0.5$	Hacia arriba	$(3,4)$
$1$	$y=-2(x+4)^2+3$	$-2$	Hacia abajo	$(-4,3)$
$3$	$y=–2(x+3)2+4$	$2$	Hacía arriba	$(-3,4)$
$2$	$y=-2(x+4)^2+3$	$-0.5$	Hacia abajo	$(4,3)$

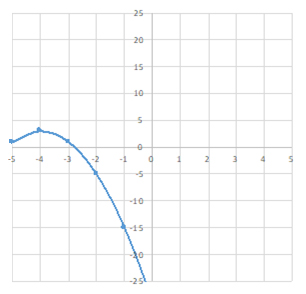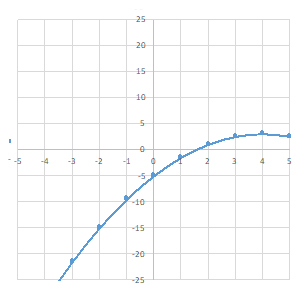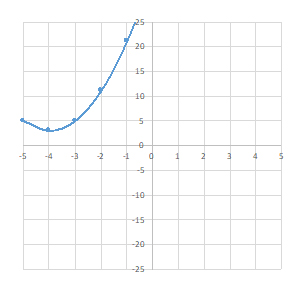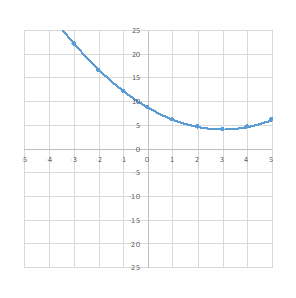Parámetros de la función cuadrática

Completa en cada espacio la información que hace falta y reflexiona sobre la forma en que obtuviste la respuesta.

	Forma general	Forma estándar	Ceros		Concavidad	Vértice	Retroalimentación
1	$y=-2x^2-30x-46$	$y=-2(x+5)^2+4$	$-6.41$	$-3.59$	Hacia abajo	Máximo $(-5, 4)$	Desde la forma general $(a)$y conociendo el vértice $(h,k)$ obtienes la forma estándar. $y=-2(x+5)^2+4$, o bien, con transformaciones algebraicas desde la forma general.
2	$y=2x^2-4x-4$	$y=2(x-1)^2$	1	1	Hacia arriba	Mínimo $(1,0)$	$y=-2x^2-4x-2$ Obtén la forma general con transformaciones algebraicas, después aplica la solución de la ecuación general de segundo grado. Ceros iguales en 1.
3	$y=-9x^2-144x+66$	$y=-9(x+8)^2-2$	$1.06$	$15.53$	Hacia abajo	Máximo $(-8,-2)$	La concavidad la obtienes desde el vértice, desde la forma estándar: $(-8,-2)$.$y=–(x–6)^2$, puedes obtenerlo desde la forma general (es un TCP) o desde el valor del vértice y sabiendo que tiene concavidad hacia abajo.
4	$y=-x^2+12x-36$	$y=(x-6)^2$	$-6$	$-6$	Hacia abajo	Máximo $(6,0)$	$y=-x(x-6)^2$, puedes obtenerlo desde la forma general (es un TCP) o desde el valor del vértice y sabiendo que tiene concavidad hacia abajo.
5	$y=2x^2-4x+4$	$y=2(x-1)^2+2$	$0.5+i$	$0.5-i$	Hacia arriba	Mínimo $(1,2)$	$y=2x^2-4x+4$, puedes obtenerlo desde la forma estándar con transformaciones algebraicas.
6	$y=5x^2-20+17$	$y=5(x-2)^2-3$	1.23	2.77	Hacia arriba	Mínimo $(2,-3)$	Las raíces se obtienen desde la forma general: $1.23$ y $2.77$ y el vértice $(2,-3)$ desde la forma general.

Parámetros de la función cuadrática

Contesta falso o verdadero a las siguientes afirmaciones.

La forma estándar me permite aplicar directamente la solución de la ecuación de segundo grado para obtener lo ceros de la ecuación sin hacer ninguna transformación.	Falso	Para resolver los ceros de la función es necesario expresar la función forma general $ax^2+bx+c$, por lo que tendría que transformarse desde $a(x-h)^2+k$.
El parámetro a en ambas formas tiene el mismo valor.	Verdadero	Tanto en la forma general $ax^2+bx+c$ como en la estándar $a(x-h)^2+k$ al realizar los despejes correspondientes podr´ñas comprobar que es la misma cantidad
En una ecuación de segundo grado, el parámetro a puede valer cero.	Falso	Para que se considere una función de segundo grado, el parámetro a, que corresponde al coeficiente de segundo grado, debe ser distinto a cero.
Los parámetros k y c indican un desplazamiento de la gráfica hacia arriba o hacia abajo, pero no necesariamente tienen el mismo valor.	Verdadero	Para resolver el trinomio de la forma estándar $a(x-h)^2+k$ con $h=0$ se tendría una función de la forma $ax^2+c$, sólo cuando $h=0, c=k,$ en los demás casos no.
El punto dónde se ubica el vértice de la función de segundo grado puede obtenerse directamente de la función en su forma general para todas las funciones cuadráticas	Falso	A partir de la forma general $ax^2+bx+c$ debe hacerse algún despeje para obtener la forma general $a(x-h)^2+k$ y así ubicar el vértice en el punto $(h,k)$
¿Sólo las gráficas cóncavas hacia arriba pueden tener una o dos soluciones?	Falso	Las funciones cóncavas (abre hacia abajo) o convexas (abre hacia arriba), pueden intersectar el eje de las $X$.