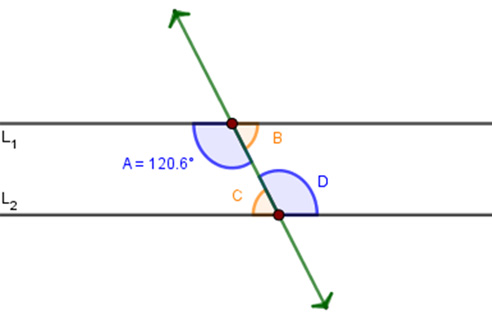
Observa con atención el siguiente video. En éste se muestran dos rectas $L_1$ y $L_2$ (en color negro); y a la derecha, se observa el punto de intersección G (en verde). La recta transversal AD (verde) corta a las rectas. En colores naranja y azul se indican los ángulos interiores ${\color{DarkOrange} {\angle A}} $ y ${\color{RoyalBlue} {\angle B}}$; cabe resaltar que se muestran los ángulos interiores del lado derecho, localizados del mismo lado que el punto de intersección.
Observa que, conforme cambia la inclinación de la recta $L_2$, el punto de intersección se desplaza; asimismo, los ángulos interiores cambian su valor, así como la suma de los ángulos interiores, ${\color{DarkOrange} {\angle A}} + {\color{RoyalBlue} {\angle B}}$; observa que en la mayoría de los casos, esta suma es menor a dos ángulos rectos (dicho en otras palabras, la suma es menor a $180^o$), es decir, ${\color{DarkOrange} {\angle A}} + {\color{RoyalBlue} {\angle B}} < 180^o$. Sin embargo, existe un caso especial en el que dicha suma es igual a $180^o$ $({\color{DarkOrange} {\angle A}} + {\color{RoyalBlue} {\angle B}} = 180^o)$, ¿has notado cuándo se presenta este caso especial?
Después de observar el video, se concluye que:
En el video anterior observaste que cuando las rectas L1 y L2 se cortan, la suma de los ángulos interiores es menor a $180^o$.
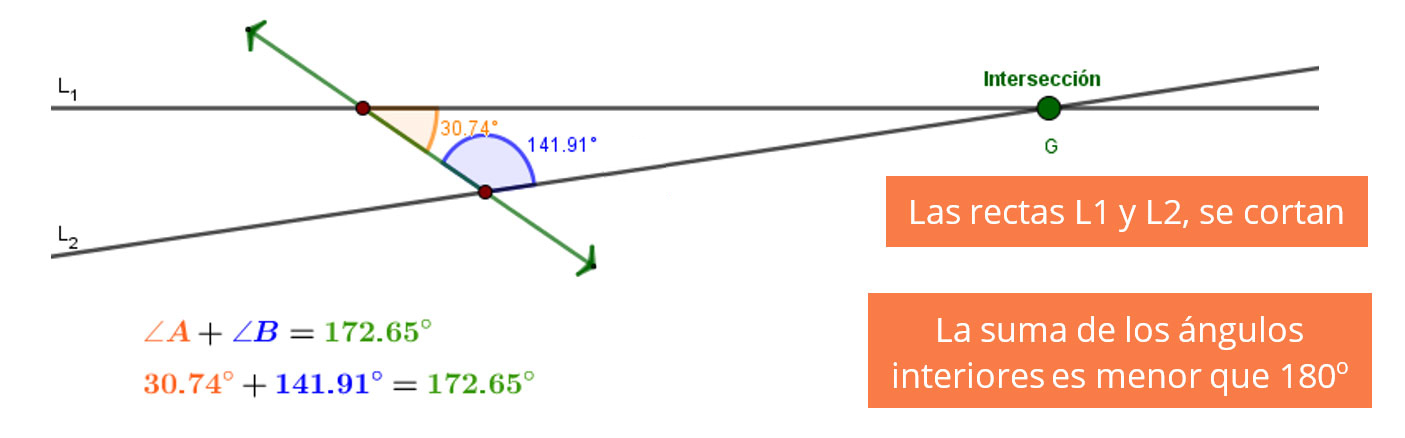
Asimismo, cuando las rectas son paralelas, la suma de los ángulos interiores es igual a $180^o$.
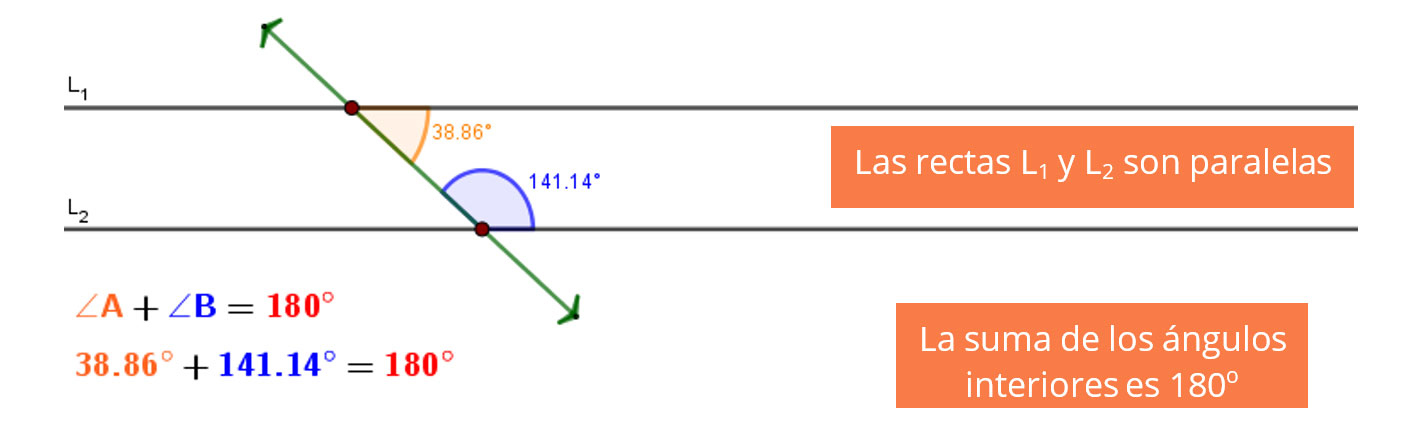

Explora el siguiente recurso GeoGebra y verifica que, cuando una recta transversal corta a dos rectas $L_1$ y $L_2$, se tiene alguno de los siguientes dos casos: 1) si la suma de los ángulos interiores del mismo lado es menor a $180^o$, entonces las dos rectas se cortan en algún punto de su prolongación; 2) cuando la suma de los ángulos interiores es igual a $180^o$ entonces las dos rectas son paralelas.
En el tratado matemático “Elementos” de Euclides, escrito cerca del año 400 a. C., se describen más de ciento ochenta definiciones, cinco postulados, así como nociones comunes o axiomas, que dan forma a la llamada Geometría Euclidiana; el quinto postulado describe la situación que hemos explorado en el recurso GeoGebra anterior.
El quinto postulado (también llamado postulado de las paralelas) enuncia que:
En los siguientes ejemplos se ilustra el postulado de las paralelas.
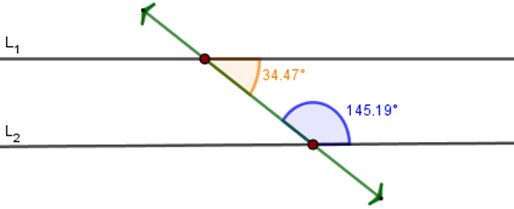
1. Indica si las rectas $L_1$ y $L_2$ son paralelas. Considera el postulado de las paralelas para hacer tus deducciones.
Solución
Como la suma de los ángulos interiores es menor a $180^o$, entonces las rectas $L_1$ y $L_2$ se cortan en sus prolongaciones; es decir, no son paralelas
${\color{DarkOrange} {\angle A}} + {\color{RoyalBlue} {\angle B}} = 179.66^o$
${\color{DarkOrange} {34.47^o}} + {\color{RoyalBlue} {145.19^o}} = 179.66^o$
2. Si las rectas $L_1$ y $L_2$ son paralelas y $\angle A = {106.33^o}$. Determina el valor del ángulo $\angle B$.
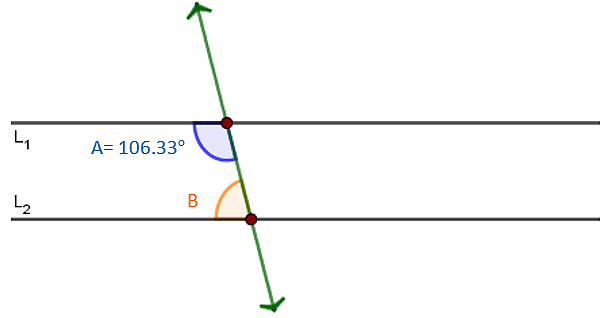
Solución
Dado que las rectas son paralelas, entonces la suma de los ángulos interiores suma $180^o$. Por lo tanto, al sumar los ángulos interiores a la izquierda de la transversal tenemos:
| Expresiones | Razones |
|---|---|
| $$\angle A + \angle B = {180^o}$$ $${106.33^o} + \angle B = {180^o}$$ $$\angle B = {180^o} - {106.33^o}$$ $$\angle B = {73.67^o}$$ | Por el postulado de las paralelas |
Utilizando el postulado de las paralelas, encuentra los ángulos que se indican. Resuelve estos cuatro planteamientos.
1. Indica los casos en los que las rectas $L_1$ y $L_2$ SÍ son paralelas. Considera el postulado de las paralelas para hacer tus deducciones.
2. Si las rectas $L_1$ y $L_2$ son paralelas y $\angle FCB = {120.7^o}$; determina el valor del ángulo correspondiente $\angle EBA$.
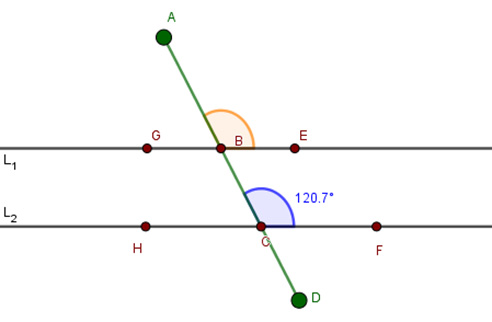
3. Si las rectas $L_1$ y $L_2$ son paralelas y $\angle BCH = {71.84^o}$; determina el valor del ángulo correspondiente $\angle ABG$.
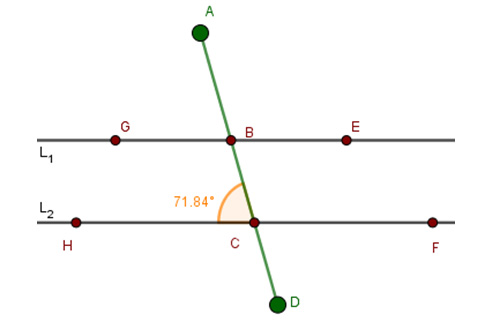
4. Si las rectas $L_1$ y $L_2$ son paralelas y $\angle A = {120.6^o}$; determina el valor del ángulo interno $\angle D$.