(ángulos alternos internos, alternos externos y correspondientes)
Aprenderás que los ángulos, clasificados por su posición relativa en dos rectas cortadas por una transversal, pueden ser alternos internos, alternos externos y correspondientes.
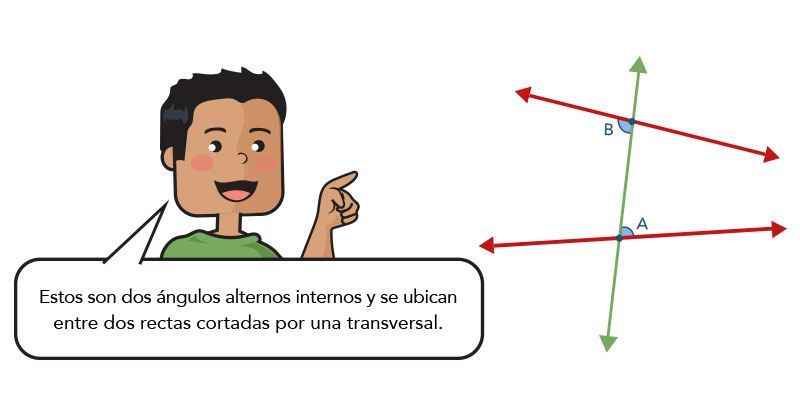
Revisa esta clasificación y los recursos GeoGebra.
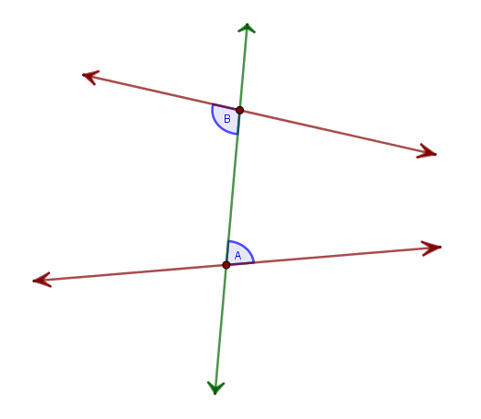
Son dos ángulos que, en una transversal que corta a dos rectas, son internos a las rectas pero alternos en la transversal.

Revisa el recurso GeoGebra .
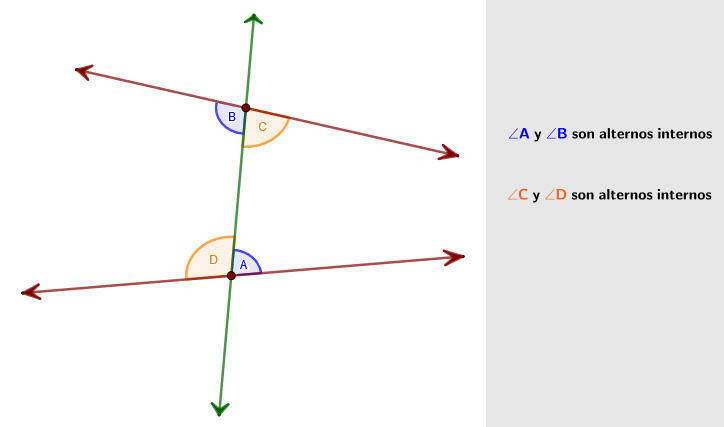
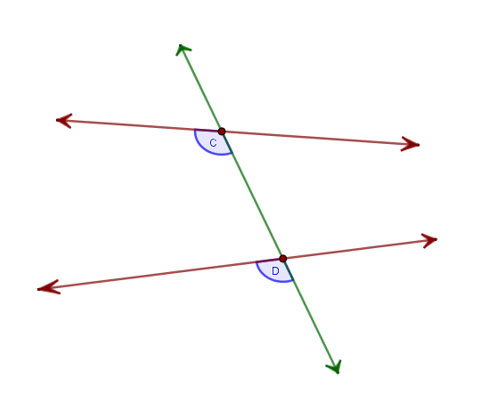
Son dos ángulos que, en dos rectas cortadas por una transversal, son externos a las rectas pero alternos en la transversal.

Revisa el recurso GeoGebra .
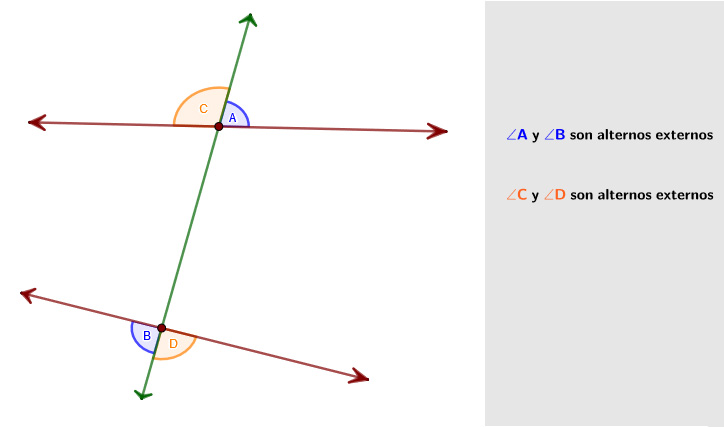
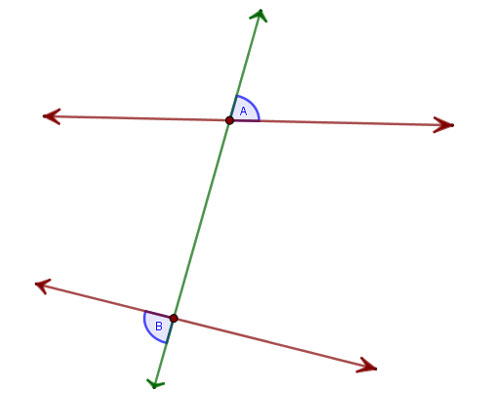
Son dos ángulos que, en dos rectas cortadas por una transversal, están del mismo lado de la transversal, pero uno es interno y el otro es externo a las dos rectas.

Revisa el recurso GeoGebra .
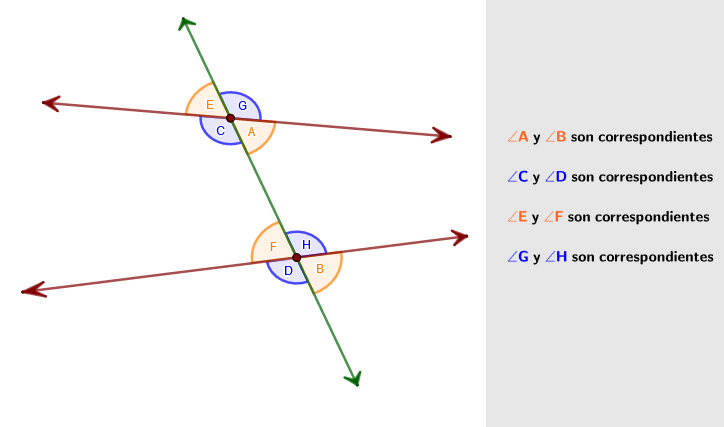
Arrastra la opción correcta al lugar que corresponde. Las respuestas correctas aparecerán en color verde. A partir de lo que observaste en el recurso interactivo anterior se puede afirmar que los:
| Tipos de ángulos | Descripción |
| Ángulos alternos externos | |
| Ángulos correspondientes | |
| Ángulos alternos internos |