El estudio de los ángulos se remonta a más de 3000 años a.C. Los pueblos mesopotámicos desarrollaron un sistema de numeración sexagesimal, que les permitió dividir la circunferencia en 360 partes iguales, cada una de ellas representa un grado sexagesimal (1°).
Asimismo, diversas culturas utilizaron las medidas de los ángulos en la construcción de grandes edificaciones y canales de agua, estaquillar parcelas de terreno, en la astronomía y en la geometría aplicada en la guerra.
Con el devenir de los años, y el consecuente desarrollo cultural y tecnológico, se desarrollaron diversos instrumentos destinados exclusivamente a la medición de ángulos y que se utilizaban en áreas diversas como astronomía, geodésica y topografía. Los primeros instrumentos de los que se tiene registro provienen de Mesopotamia, Egipto y China.
En la actualidad, la medición de los ángulos tiene aplicaciones en prácticamente todas las ciencias y en la tecnología, por lo que citar todos los ejemplos sería una lista casi interminable. En la figura 1 se muestra una prótesis de pie desarrollada en el Instituto Tecnológico de Massachusetts (MIT, por sus siglas del inglés) ; las imágenes muestran que para el diseño es importante conocer los ángulos de movimiento del pie.
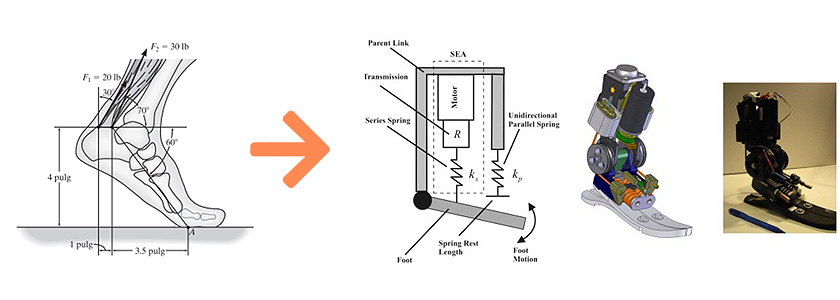
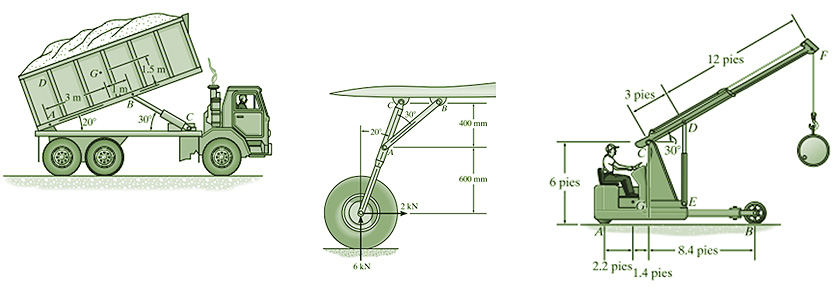
La figura 2 muestra que para el diseño de diversos sistemas mecánicos también es imprescindible en conocimiento de los ángulos involucrados.
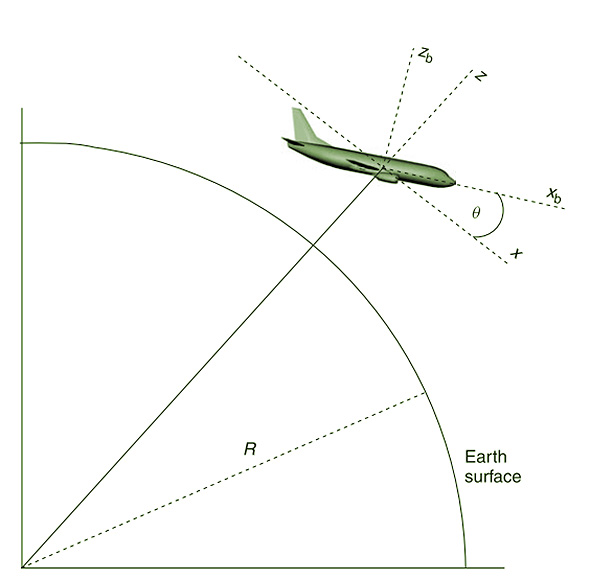
Otra aplicación de los ángulos se tiene en el análisis, diseño y programación de videojuegos y simuladores de vuelo (Allerton, 2009).
En este objeto de aprendizaje estudiarás los ángulos, su calificación y sus relaciones; también conocerás e identificarás los tipos de ángulos que se forman entre dos rectas cortadas por una transversal. Concluirás que en el caso que dos rectas paralelas sean cortadas por una transversal, los ángulos alternos internos son congruentes e inversamente. A finalizar aplicarás los conceptos aprendidos en la resolución de problemas.


