Sistema decimal
El sistema de numeración que utilizamos incluye diez dígitos ${ 0,1,2,3,4,5,6,7,8,9}$ para representar cualquier cantidad. Se conoce como sistema base $10$ o decimal y la posición en la representación indica una cantidad numérica distinta, así tenemos unidades $(1=10^0)$, decenas $(10=10^1)$, centenas $(100=10^2)$, millares $(1000=10^3)$, y así sucesivamente como potencias de la base, $10$. Así, el sistema de numeración incluye a los números naturales ($\mathbb{N}$, números positivos sin incluir al cero) y al cero. Así, la representación sería la siguiente:
| $10^4$ | $10^3$ | $10^2$ | $10^1$ | $10^0$ |
|---|---|---|---|---|
| 10000 | 1000 | 100 | 10 | 1 |
| ... | MILLARES | CENTENAS | DECENAS | UNIDADES |
| 7 | 8 | 2 | 2 | 1 |
|---|---|---|---|---|
| +70000 | +8000 | +100 | +20 | +1 |
El número 78,221 (setenta y ocho mil doscientos veintiuno) incluye los dígitos ${1,2,7,8}$ que están incluidos o pertenecen a los dígitos decimales ${ 0,1,2,3,4,5,6,7,8,9 }$. Hay que notar que el dígito 2 aparece dos veces en este número, pero por la posición que ocupan, la primera ocurrencia vale $200~(2 \times 10^2)$ y la segunda aparición vale $20~(2 \times 10^3)$.
Observa la siguiente animación para que recuerdes cómo funciona un sistema posicional. No olvides que hacia el lado derecho del punto decimal los exponentes incrementan de derecha a izquierda. Desde el punto decimal, la primera posición comienza a numerarse desde cero, esta posición corresponde a las unidades en cualquier sistema de numeración.
| $10^7$ | $10^6$ | $10^5$ | $10^4$ | $10^3$ | $10^2$ | $10^1$ | $10^0$ | |
|---|---|---|---|---|---|---|---|---|
| 10000000 | 1000000 | 100000 | 10000 | 1000 | 100 | 10 | 1 | |
| +0 | +0 | +0 | +0 | +0 | +300 | +20 | +6 | =326 |
Se puede agregar el signo “–“ para incluir a los números negativos y tener a los números enteros $\mathbb{Z}$.
Para las representaciones con punto decimal, las potencias a la derecha del punto decimal se numeran desde $–1$, $–2$, $–3$, y así sucesivamente, correspondiendo a $0.1=10^{-1}=\tfrac{1}{10}$, $0.01=10^{-2}=\tfrac{1}{100}$, $0.1=10^{-3}=(\tfrac{1}{1000})$, y así sucesivamente a las décimas, centésimas, milésimas, ...
| $.$ | $10^{-1}$ | $10^{-2}$ | $10^{-3}$ | ... |
|---|---|---|---|---|
| 0.1 | 0.01 | 0.001 | ... | |
| PUNTO DECIMAL | DÉCIMAS | CENTÉSIMAS | MILÉSIMAS | ... |
| $.$ | $1$ | $2$ | $2$ | |
|---|---|---|---|---|
| +70000 | 0.1 | 0.02 | 0.002 |
Todos estos sistemas son posicionales. Esto es, la posición de una cifra indica su valor en función de elevar la base a una potencia determinada de acuerdo a su ubicación en la representación numérica.
Sistema binario
En la práctica, las computadoras digitales se diseñan de manera simple considerando únicamente dos estados. Debido a la restricción física de los componentes y a que en muchas ocasiones la lógica humana tiende a ser binaria (esto es, cierto o falso, si o no, encendido o apagado), los componentes digitales fueron diseñados para tomar dos valores discretos, por lo que se dice que son binarios.
El sistema binario o sistema de numeración base 2, es también un sistema de numeración posicional, igual que el decimal, pero sólo utiliza dos símbolos: ${ “0”, “1” }$. Por lo tanto, para poder representar el mayor número de información al tener menos símbolos se tienen que utilizar más cifras, y los dígitos tendrán un valor distinto de acuerdo con la posición que ocupen.
Las computadoras digitales utilizan el sistema de números binarios que tiene dos dígitos: 0 y 1. Un digito binario se denomina bit (que es una abreviación de binary digit). Si esto se visualiza como un circuito con un interruptor y un pequeño diodo emisor de luz (LED), el interruptor abierto representa el estado de apagado y el 1.
Completa los espacios con la información que hace falta. Observa el siguiente circuito: ¿Al activar o desactivar el interruptor que sucede con la lámpara?
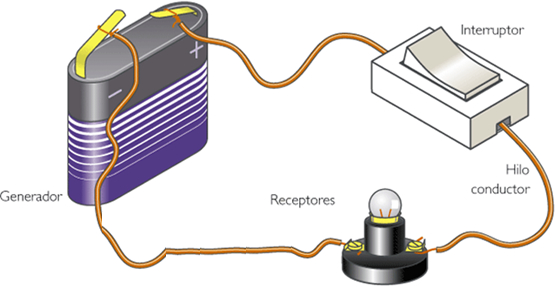
Escribe la respuesta correcta en los espacios para completar el procedimiento. Otro ejemplo utilizando el sistema binario:
Otro ejemplo utilizando el sistema binario:
Sistemas octal y hexadecimal
El sistema de numeración octal utiliza 8 dígitos para su representación, el cual incluye el rango de números del 0 al 7. El sistema de numeración octal también es utilizado en la computación por tener una base que es potencia exacta de $2 {(2^3)}$. Esta característica permite que la conversión a binario o viceversa sea simple.
El sistema de numeración hexadecimal utiliza los siguientes dígitos para su representación (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, F), esto corresponde la numeración del 0 al 15 en el sistema decimal.
Cabe resaltar, que para contar con un sistema de numeración posicional es necesario contar con las siguientes características:
- El uso del cero.
- Un símbolo distinto para representar cada dígito.
- Cada dígito toma un valor distinto dependiendo de su ubicación, como potencias de la base.
Por lo anterior, para representar dígitos del décimo en adelante, se tomó la convención de utilizar letras. Así, el onceavo dígito se representa con la letra “A”, el doceavo con la letra “B”, y así sucesivamente.
Para su representación binaria se requieren cuatro bits para representar cada dígito hexadecimal númerico.
A continuación se muestra la tabla de equivalencias entre los diferentes sistemas de numeración.
| Decimal | Binario | Octal | Hexadecimal |
|---|---|---|---|
| 0 | 0000 | 00 | 0 |
| 1 | 0001 | 01 | 1 |
| 2 | 0010 | 02 | 2 |
| 3 | 0011 | 03 | 3 |
| 4 | 0100 | 04 | 4 |
| 5 | 0101 | 05 | 5 |
| 6 | 0110 | 06 | 6 |
| 7 | 0111 | 07 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |


