Una necesidad importante en la representación de cantidades numéricas en la computadora, corresponde al uso de las fracciones. La representación de las fracciones en la computadora se hace a través del punto binario.
De manera similar al sistema decimal cuando utilizamos el punto decimal, las cifras que aparecen inmediatamente a la izquierda del punto utilizan potencias negativas y van disminuyen de uno en uno, por ejemplo 0.71875 se compondría con las siguientes partes de 7 décimos: $\tfrac{7}{10} = 7 \times 10^{-1}$, $1$ centésimo $\tfrac{1}{100} = 1 \times 10^{-2}$, $8$ milesimos $\tfrac{8}{1000} = 8 \times 10^{-3}$, $7$ diezmilésimos $\tfrac{7}{10000} = 7 \times 10^{-4}$ y 5 cienmilésimos $\tfrac{7}{10000} = 7 \times 10^{-4}$, en potencias negativas de la base. Así se interpretaría de la cantidad fraccionaria a su equivalente en decimal:
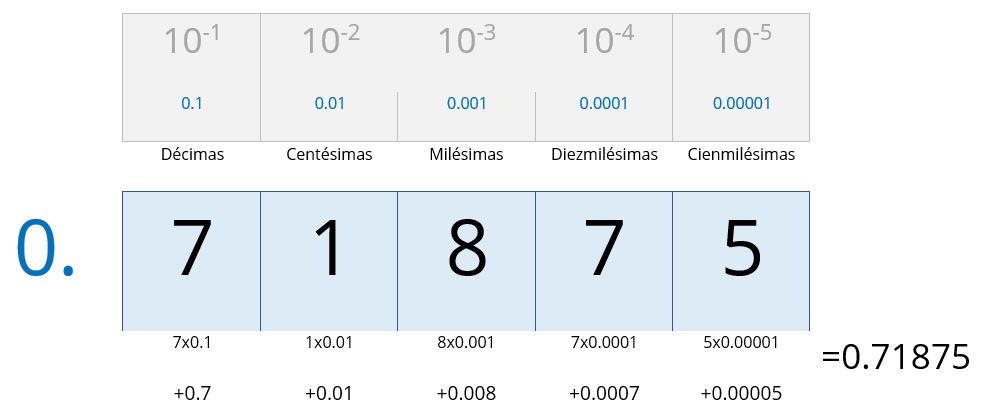
Para el caso de un número en binario:
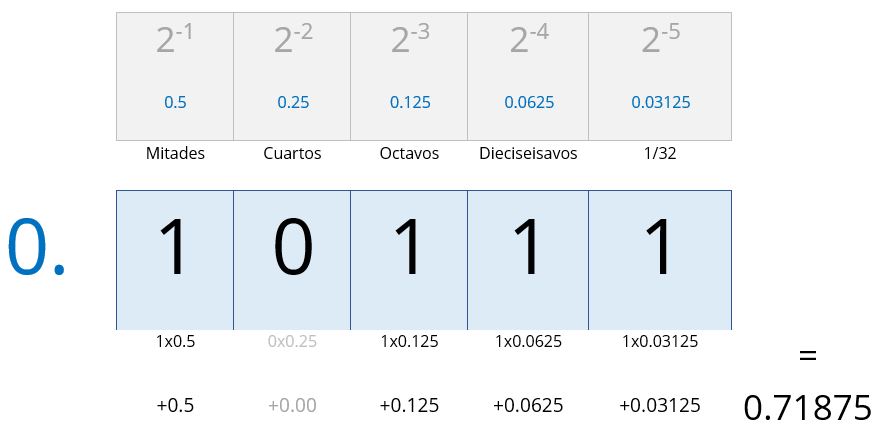
Para el caso de un número en hexadecimal:

El proceso contrario, que consiste en obtener la parte fraccionaria de una cantidad en decimal en otra potencia, es el proceso contrario al que usábamos, en las conversiones anteriores. Si analizamos la conversión de decimal, correspondería a ir moviendo las cifras a la izquierda del punto decimal y esto se logra multiplicando por 10, por la base.
Así, este proceso se reduce a:
- La cantidad fraccionaria (decimales después del punto) se multiplican por la base deseada.
- La parte entera se coloca a la derecha del punto o de la última cifra obtenida.
- Se repite el proceso sólo con la parte fraccionaria.
Ejemplo: “convertir” 0.71875 de base 10 a decimal:
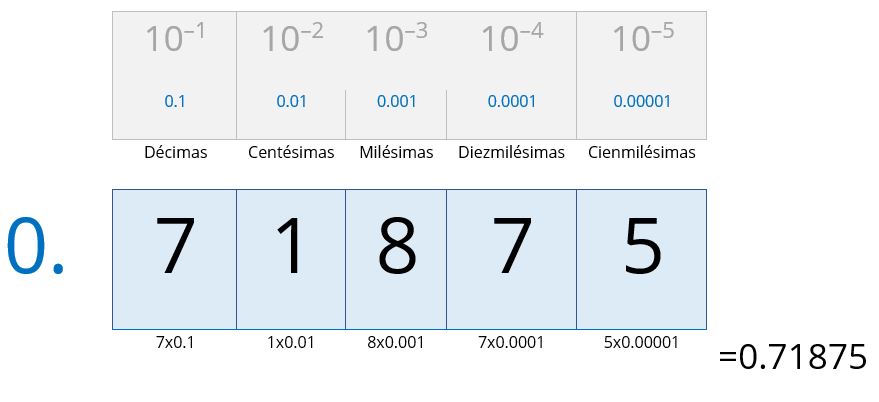
-
A partir de la parte fraccionaria original0.71875
-
Recorre el punto decimal de la parte fraccionaria (0.71875) multiplicando por la base (10).
0.71875 x 10 = 7.1875
7 será el dígito después del punto y 0.1875 la parte fraccionaria.
-
Repite: Recorre el punto decimal de la parte fraccionaria (0.1875) multiplicando por la base (10).
0.1875 x 10 = 1.875
1 será el dígito después del punto y 0.875 la parte fraccionaria.
-
Repite: Recorre el punto decimal de la parte fraccionaria (0.875) multiplicando por la base (10).
0.875 x 10 = 8.75
8 será el dígito después del punto y 0.75 la parte fraccionaria.
-
Repite: Recorre el punto decimal de la parte fraccionaria (0.75) multiplicando por la base (10).
0.75 x 10 = 7.5
7 será el dígito después del punto y 0.5 la parte fraccionaria.
-
Repite: Recorre el punto decimal de la parte fraccionaria (0.5) multiplicando por la base (10).
0.5 x 10 = 5.0
5 será el dígito después del punto y 0.0 la parte fraccionaria.
-
Repite: Recorre el punto decimal de la parte fraccionaria (0) multiplicando por la base (10).
El procedimiento se detiene cuando la parte fraccionaria es 0 o bien hasta un número de dígitos proporcionados por el problema.
-
Escribir las cantidades después del punto decimal en el orden que se obtuvieron.
0.71875
Escribe la respuesta correcta en los espacios que corresponden para completar el procedimiento:
Ejercicio 1
Obtener la representación en binario de $0.71875_{10}$:
Ejercicio 2
Obtener la representación en hexadecimal de $0.71875_{10}$:
Ejercicio 3
Obtener la representación en base $16$ de $0.33_{10}$. Si no consigue una representación finita, utilice sólo 8 dígitos hexadecimales.
Tipos de datos
Cuando hablamos de representaciones de los números y su almacenamiento en la memoria de las computadoras, hay que definir el tamaño que ocuparán, por lo tanto tendrán un número finito de dígitos (binarios, bits) para su representación. Una mayor precisión requerirá mayor capacidad de procesamiento y circuitos más complejos para su implementación.
Los números reales estarían representados por cierta cantidad de bits, que le darían una precisión y un acercamiento a la representación en decimal que conocemos de los números. Mientras mayor cantidad de bits se tengan de precisión, mayor será la cantidad de números que puedan representarse y menor el error o diferencia entre la representación decimal o fraccionaria.
No existen números irracionales en las computadoras, ya que siempre habrá una cantidad finita de números. Recuerda cuando las cifras decimales se repetían en series infinitas o con los números irracionales, muchas representaciones en binario no serán racionales, pero no podrán ser infinitas, ya que para la computadora tienen que guardarse en espacios finitos, generalmente en múltiplos de 8 bits (byte, word, double word, quad-word, 128 bits, 256 bits, …)
En el siguiente diagrama se acomodaron los tipos de datos de punto flotante y enteros. Algunos lenguajes de programación hacen una diferenciación entre tipos de datos entre enteros con signo (signed) y sin signo (unsigned); aunque la tendencia es implementar números con signo en todos los casos.

Los números o tipos de dato que aparecen en azul, corresponden a los enteros y los que están en rojo a los de punto flotante, que corresponderían a los reales. Las intersecciones de los conjuntos se colocaron en función de que la precisión de una representación de punto flotante pueda contener a todos los números representados por el tipo de dato entero sin pérdida de precisión de acuerdo al estándar IEEE 754.
El término “palabra” (word) corresponde a la arquitectura de las computadoras, aunque actualmente se reconoce como el valor de la arquitectura del procesador y del sistema operativo, en 2020 el más común es de 64 bits.


