Conversión de octal a binario
Se efectúa el proceso inverso al elaborado de binario a octal. Cada dígito octal se sustituye por sus tres dígitos binarios, que se pueden consultar en la tabla de equivalencias entre los diferentes sistemas de numeración. Para ello, recordemos la tabla que se construye convirtiendo de octal a decimal y de decimal a binario.
Escribe los valores que faltan para completar el procedimiento.
Por ejemplo, si quisieras convertir $70215_8$ a binario, tendrías que sustituir, en el mismo orden los dígitos:
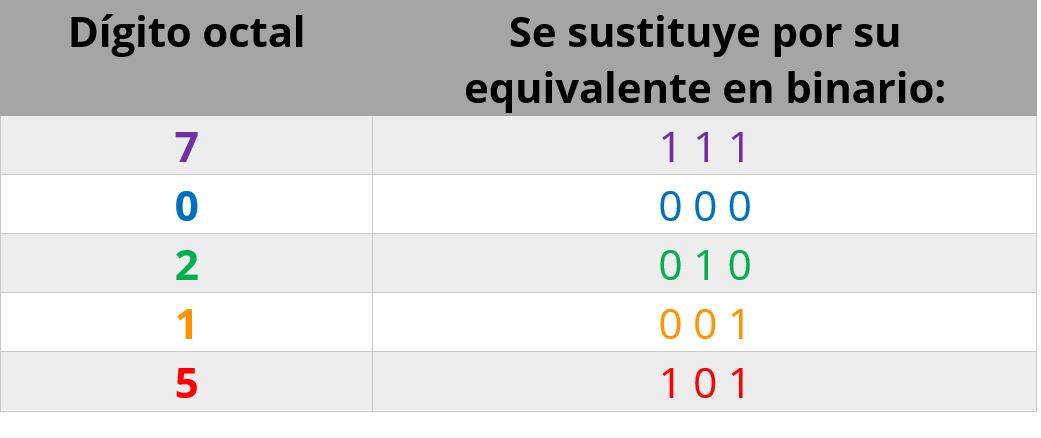
Por lo que ${\color{Purple}7} {\color{Blue}0} {\color{Green}2} {\color{Orange}1} {\color{Red}5}_8 = {\color{Purple}111}{\color{Blue}000} {\color{Green}010} {\color{Orange}001} {\color{Red}101}_2$
Verificando por el procedimiento “largo”, convertimos todo el número de octal a decimal:
| $8^4$ | $8^3$ | $8^2$ | $8^1$ | $8^0$ | Base elevada a la posición |
|---|---|---|---|---|---|
| 4096 | 512 | 64 | 8 | 1 | |
| 7 | 0 | 2 | 1 | 5 | Dígitos ocupados |
| +7x4096 | +0x512 | +2x64 | +1x8 | +5x1 | = |
| +28672 | +0 | +128 | +8 | +5 | 28813 |
Posteriormente de decimal a binario:
| Base final | |||
| 2 | |||
| Base 10 | 28813 | 1 |
|
| 14406 | 0 | ||
| 7203 | 1 | ||
| 3601 | 1 | ||
| 1800 | 0 | ||
| 900 | 0 | ||
| 450 | 0 | ||
| 225 | 1 | ||
| 112 | 0 | ||
| 56 | 0 | ||
| 28 | 0 | ||
| 14 | 0 | ||
| 7 | 1 | ||
| 3 | 1 | ||
| 1 | 1 | ||
| 0 | |||
Y obtenemos el mismo resultado: ${\color{Purple}7} {\color{Blue}0} {\color{Green}2} {\color{Orange}1} {\color{Red}5}_8 = {\color{Purple}{111}} {\color{Blue}{000}} {\color{Green}{010}} {\color{Orange}{001}} {\color{Red}{101}}_2$, puede observarse que el método abreviado es más rápido y llegamos al mismo resultado.
| Número en octal: | 7 | 0 | 2 | 1 | 5 |
|---|---|---|---|---|---|
| Número en binario: | 111 | 000 | 010 | 001 | 101 |
Escribe los valores que faltan para completar el procedimiento.
Ejercicio 1
Realice la conversión de $56_8$ a binario.
Sustituyendo cada dígito octal por su representación en binario:
En la siguiente pantalla se explica la Conversión de binario a hexadecimal.


