Conversión de enteros sin signo de decimal a cualquier base

La información está representada en las computadoras digitales en grupos de bits, sin embargo para el ser humano operar información en el sistema binario resulta complicado y poco entendible para la mayoría, por lo que existen métodos de conversión entre un sistema y otro permitiendo con ello la interacción entre los diferentes sistemas de numeración.

Conversión de “decimal a decimal”

Dado un número, al dividirlo entre la base nos quedará un residuo que corresponde a las unidades, si continuas de esta manera obtendrás las decenas (ya que tendrás la parte entera del residuo de divisor dos veces entre 10), después las centenas y obtendrás el primer dígito del residuo de dividir tres veces entre la base.

Observa el siguiente ejemplo donde utilizaremos este procedimiento para convertir un número de decimal a decimal, es decir, de base 10 a base 10. Convertiremos 8221 de base 10 a base 10.

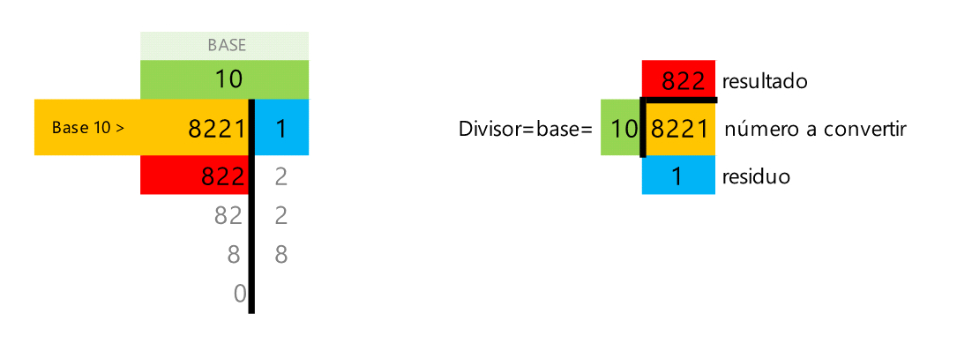
Unidades Decenas Centenas Millares Concluyendo Resultado

En una división, coloque el número original como dividendo, la base como divisor.
El resultado (entero) de la división es el siguiente número por dividir, colóquelo abajo del número original.
El residuo colóquelo al lado derecho del número que acaba de dividir.
Repita.

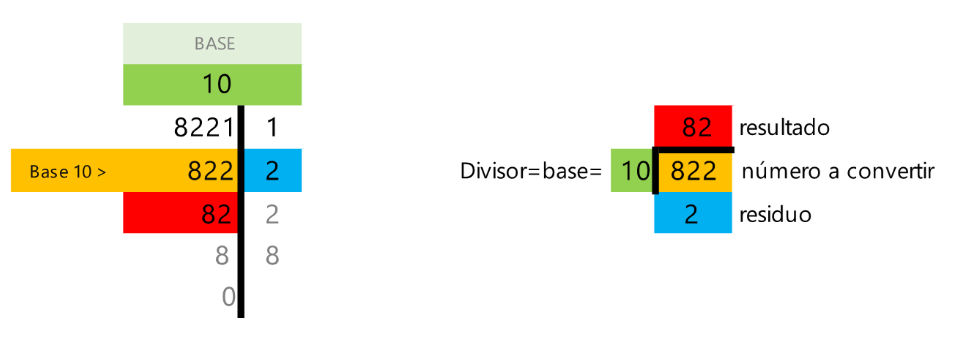
En una división, coloque el número original como dividendo, la base como divisor.
El resultado (entero) de la división es el siguiente número por dividir, colóquelo abajo del número original.
El residuo colóquelo al lado derecho del número que acaba de dividir.
Repita.

En una división, coloque el número original como dividendo, la base como divisor.
El resultado (entero) de la división es el siguiente número por dividir, colóquelo abajo del número original.
El residuo colóquelo al lado derecho del número que acaba de dividir.
Repita.

En una división, coloque el número original como dividendo, la base como divisor.
El resultado (entero) de la división es el siguiente número por dividir, colóquelo abajo del número original.
El residuo colóquelo al lado derecho del número que acaba de dividir.
Repita.

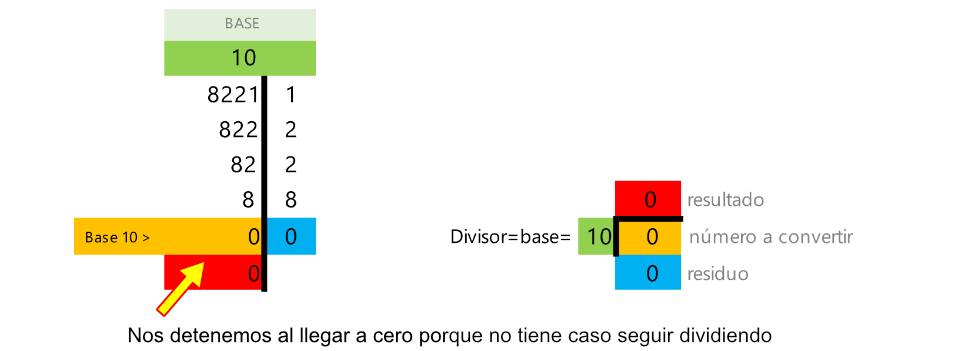
En una división, coloque el número original como dividendo, la base como divisor.
El resultado (entero) de la división es el siguiente número por dividir, colóquelo abajo del número original.
El residuo colóquelo al lado derecho del número que acaba de dividir.
Repita.

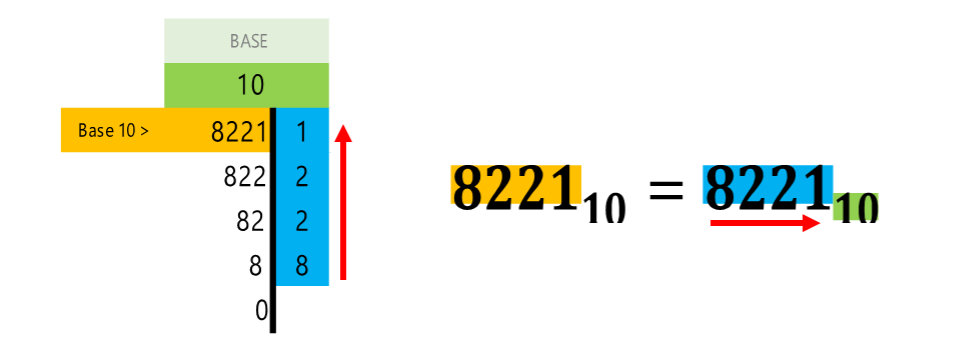
Retome la columna de los residuos, escríbalos de abajo para arriba y obtendrá el resultado. El número original (en base 10) es igual a los dígitos de los residuos escritos (siguiendo el orden de abajo hacia arriba).

Escribir

Realiza la siguiente conversión de decimal a base 10 y escribe en los espacios los valores que hacen falta.

Ejercicio 1

Convertir 1245 de decimal a base 10:

Es necesario que escribas las respuestas para recibir retroalimentación.

	Base final
	10
Base 10	1245	5
	124	4
	12	2
	1	1
	0	0
$1245_{10}=$		1245₁₀

Ejercicio 2

Convertir 365 de decimal a base 10:

Conversión de decimal a binario

A continuación se describe el procedimiento para realizar la conversión del sistema decimal al sistema binario, y en general este procedimiento permitirá convertir del sistema decimal a cualquier otro.

Para convertir un número de decimal a cualquier base: se divide el número entre la base a convertir e ir acumulando los residuos hasta que el cociente sea 0. El número buscado se acomoda partiendo del último residuo hasta el primero.

Ejemplo: $55_1{10}=X_2$

	Base final
	2
Base 10	55	1
	27	1
	13	1
	6	0
	3	1
	1	1
	0

Resultado: $55_{10}=110111_2$

Observa el siguiente video para que veas el proceso de conversión de decimal a binario, en general es el mismo para convertir de decimal a cualquier base.

Escribir

Con los siguientes ejercicios verificarás si aprendiste el procedimiento para convertir la representación de los números, de decimal a binario.

Escribe la respuesta correcta en los espacios para completar el procedimiento.

Ejercicio 1

Convertir 149 de decimal a binario:

	Base final
	2
Base 10	149	1
	74	0
	37	1
	18	0
	9	1
	4	0
	2	0
	1	1
	0

$149_{10}=$10010101 ₂

Ejercicio 2

Convertir 53 de decimal a binario (base 2):

Conversión de decimal a octal

El siguiente ejemplo se muestra el procedimiento para la conversión del sistema decimal al sistema octal (base 8).

Ejemplo: $9877_{10}$ convertirlo a octal:

	Base final
	8
Base 10	9877	5
	1234	2
	154	2
	19	3
	2	2
	0

$9877_{10}=23225_8$

Escribir

Con los siguientes ejercicios verificarás si aprendiste el procedimiento para convertir la representación de los números de decimal a binario.

Escribe la respuesta correcta en los espacios para completar el procedimiento.

Ejercicio 1

Convertir 149 de decimal a octal:

Ejercicio 3

Convertir $61902_{10}$ da base 8: 170716₂

Retroalimentación

	Base final
	8
Base 10	61902	6
	7737	1
	967	7
	120	0
	15	7
	1	1
	0

Conversión de decimal a hexadecimal

En los siguientes ejemplos se muestra el procedimiento para la conversión del sistema decimal al sistema octal.

Ejemplo:

$9877_{10}$ convertirlo a hexadecimal (base 16).

	Base final
	16		HEX
Base 10	9877	5	5
	617	9	9
	38	6	6
	2	2	2
	0

Resultado: $9877_{10} = 2695_8$

Ejemplo:

$32197_{10}$ convertirlo decimal a hexadecimal.

	Base final
	16		HEX
Base 10	32197	5	5
	2012	12	C
	125	13	D
	7	7	7
	0

Resultado: $32197_{10}=7DC5_{16}$

Recuerde que los residuos del 10 al 15 tienen una representación en hexadecimal con las letras de la A a la F ($10_{10} = A_{16}$, $11_{10} = B_{16}$, $12_{10} = C_{16}$, $13_{10} = D_{16}$, $14_{10} = E_{16}$ y $15_{10} = F_{16}$)

Escribir

Con los siguientes ejercicios verificarás si aprendiste el procedimiento para convertir la representación de los números de decimal a hexadecimal.

Escribe la respuesta correcta en los espacios para completar el procedimiento.

Ejercicio 1

Completa los espacios en blanco de la siguiente conversión del número decimal 831 a hexadecimal:

Conversión de enteros sin signo de decimal a cualquier base

Síguenos

Sitios de interés

Nosotros

Escolares

Newsletter

	Base final
	16		HEX
Base 10	815	15	F Recuerda que el residuo: $15_{10} = F_{16}$
	51	3	3
	3	3	3
	0