Velocidad instantánea
Este problema fue estudiado ampliamente en la antigüedad por los matemáticos para determinar la velocidad instantánea de un objeto en un tiempo específico, consideraron velocidades medias (promedios) para estimar la velocidad instantánea y lo formalizaron con el proceso de límite de una función, aunado con los hallazgos obtenidos en el campo de la Física, tales como, la aceleración de los cuerpos que son atraídos por la fuerza de gravedad, en nuestro planeta su valor es aproximadamente $10\ \frac{m}{s^2}$, la velocidad de un objeto en caída libre es $10t\ \frac{m}{s}$ y la función altura está dada por $s\left(t\right)=s_0+v_ot+\frac{1}{2}gt^2$, donde la altura está dada en metros (también puede ser en pies) y el tiempo en segundos (s). La velocidad media (promedio) como recordarás se obtiene con la expresión $v_m=\frac{s\left(t_2\right)-s\left(t_1\right)}{t_2-t_1}$ , para ejemplificar su aplicación consideremos que un objeto se deja caer libremente desde una torre que tiene 20 metros de altura y se quiere obtener la velocidad instantánea en $t=1$ s.
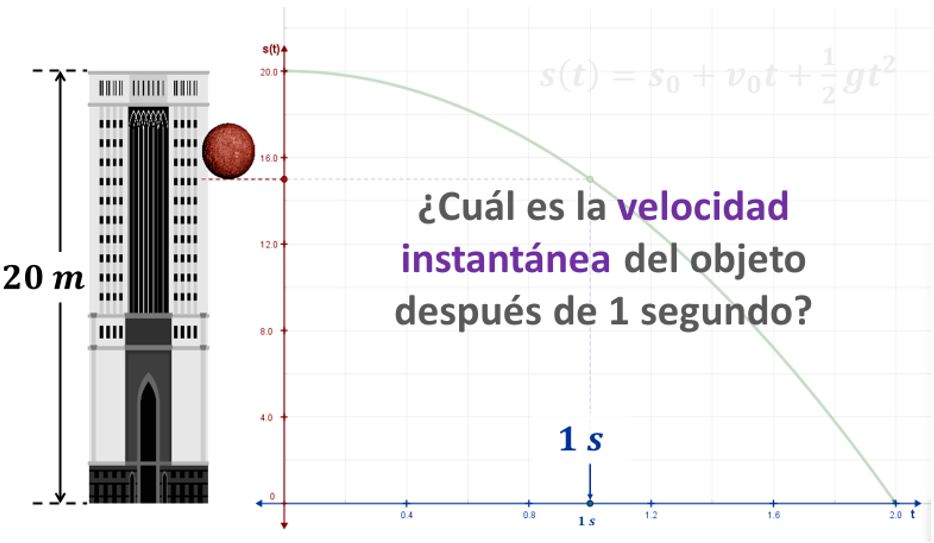
a) Graficación de la función altura
La trayectoria que sigue el movimiento de un objeto en caída libre es una línea recta, sin embargo, su representación gráfica altura versus tiempo es $s\left(t\right)=s_0+v_ot+\frac{1}{2}gt^2$. Como el movimiento del objeto es hacia abajo, consideramos la aceleración de la gravedad con signo negativo y al sustituir los datos en la función altura obtenemos $s\left(t\right)=20-5t^2$, puesto que la posición inicial del objeto es de 20 metros y la velocidad inicial $v_o=0$ ya que el objeto se deja caer sin aplicarle ninguna velocidad. La trayectoria y función se muestran en la figura, para una mayor comprensión de la situación del problema explora el recurso GeoGebra y visualiza el video.
En el recurso GeoGebra se presentan diferentes posiciones en la caída libre del objeto, aunado con el apoyo de tu imaginación geométrica observarás que al arrastrar el punto P hasta chocar impactarse con el suelo pasa por infinitos puntos, siendo ésta una característica de los procesos infinitos.
Con base en esto, contesta las siguientes preguntas:
b) Velocidad instantánea
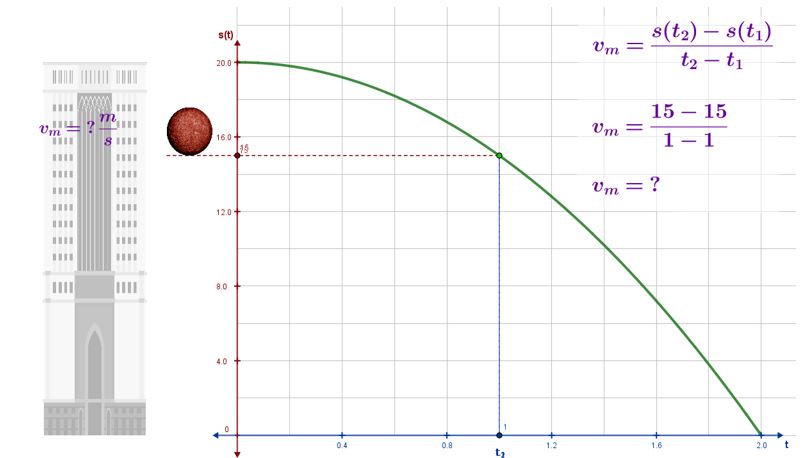
¿Cuál es la velocidad instantánea del objeto en un segundo?
Para responder la pregunta debes calcular la velocidad media en los intervalos de tiempo $\left[t_1,t_2\right]=\left[0,1\right]$, tal que $t_1$ tiende a $t_2$ (aproximación por la izquierda $t_1\longrightarrow t_2^-$) y luego en el intervalo $\left[t_2,t_1\right]=\left[1,2\right]$, tal que, $t_1$ tiende a $t_2$ (aproximación por la derecha $t_1\longrightarrow t_2^+$), con base en éstas estimar la velocidad instantánea a través de velocidades promedio que se obtienen con la expresión $v_m=\frac{s\left(t_2\right)-s\left(t_1\right)}{t_2-t_1}$. En el video se explicaron los procesos algebraicos para determinar la velocidad instantánea del objeto en el tiempo $t_1$ s.
Con base en el video y recurso GeoGebra observaste que las velocidades promedio por la izquierda y por derecha, tienen como límite la velocidad instantánea cuando el tiempo $t_1$ se aproxima al tiempo $t_2$.
Con base en esto y tu intuición matemática. Completa la siguiente tabla para evaluar tu comprensión del proceso infinito relacionado con la obtención de la velocidad instantánea, mediante las velocidades promedio por la izquierda y por la derecha en $t=1$ s. Escribe en las tablas los datos que faltan para ambas aproximaciones, las flechas del penúltimo renglón significan tiende a, tanto como se quiera.
Aproximación a la velocidad instantánea con velocidades promedio por la izquierda
Con base en la información presentada en la tabla y tu intuición matemática, contesta las siguientes preguntas, la respuesta escríbela en los recuadros de la tabla.
Aproximación a la velocidad instantánea con velocidades promedio por la derecha
Con base en la información presentada en la tabla y tu intuición matemática, contesta las siguientes preguntas, la respuesta escríbela en los recuadros de la tabla.
c) Notación de la velocidad instantánea como un proceso infinito
En este apartado pasamos a la representación simbólica de la velocidad instantánea mediante velocidades promedio del objeto en el tiempo $t=1$ s.
La simbología matemática para representar el límite de las velocidades promedio es la siguiente:
Cuando $t_1\rightarrow{t_2}^-$, $v_m\rightarrow v_i$, además, cuando $t_1\rightarrow{t_2}^+$, $v_m\rightarrow v_i$
De manera formal se utiliza la notación de límite por la izquierda y por la derecha:
$\lim_{t_{1}\to {t_{2}}^{-}}\frac{s\left(t_2\right)-s\left(t_1\right)}{t_2-t_1}=v_{i}$ y $\lim_{t_{1}\to {t_{2}}^{+}}\frac{s\left(t_1\right)-s\left(t_2\right)}{t_1-t_2}=v_{i}$
Ahora como $\lim_{t_{1}\to {t_{2}}^{-}}\frac{s\left(t_2\right)-s\left(t_1\right)}{t_2-t_1}=\lim_{t_{1}\to {t_{2}}^{+}}\frac{s\left(t_1\right)-s\left(t_2\right)}{t_1-t_2}=v_{i}$ se concluye que $\lim_{t_{1}\to {t_{2}}}\frac{s\left(t_2\right)-s\left(t_1\right)}{t_2-t_1}=v_{i}=-10\frac{m}{s}$.
Cabe mencionar que la velocidad instantánea se obtuvo para un tiempo en particular, sin embargo, se puede generalizar para cualquier tiempo aplicando el concepto de la derivada de una función estudiado en el Objeto de Aprendizaje “Variación y razón de cambio promedio e instantánea de una función”; el cual te sugerimos revises.