En este apartado vamos a sistematizar el análisis de las funciones alrededor de uno de sus puntos a un contexto más general, el concepto intuitivo del límite de una función.
Con base en el análisis de la función alrededor de uno de sus puntos a través de los registros tabular, gráfico y algebraico, éstos apuntaron en la misma dirección y permitieron la obtención del límite de la función alrededor de uno de sus puntos, mediante la igualdad de los límites laterales – límite por la izquierda y límite por la derecha alrededor de un punto en particular-, los cuales precisamos en un contexto más amplio, la definición intuitiva del límite de una función. Los límites laterales se representan con las siguientes expresiones:
- La expresión matemática $\lim_{x\to a^{-}}{f\left(x\right)=L}$, significa el límite de la función por la izquierda.
- La expresión matemática $\lim_{x\to a^{+}}{f\left(x\right)=L}$, significa el límite de la función por la derecha.
- Si $\lim_{x\to a^{-}}{f\left(x\right)=\lim_{x\to a^{+}}{f\left(x\right)}}$, entonces $\lim_{x\to a}{f\left(x\right)=L}$.
Con base en el estudio de los apartados anteriores y los aprendizajes que lograron los estudiantes, estamos en posibilidades para la formulación de la definición intuitiva del límite de una función en uno de sus puntos, tal como, se menciona a continuación:
La expresión matemática $\lim_{x\to a}{f\left(x\right)=L}$, la utilizamos en este material para la definición intuitiva del límite de una función y significa que los valores de la función $f\left(x\right)$ los podemos hacer lo suficientemente cercano a $L$ (es un número real) como queramos, siempre que para toda $x\neq a$ esté lo suficientemente cercano a $a$, tal como se ilustra en el video anterior, en el que se explica el concepto de la definición mencionada, también mediante el recurso GeoGebra.
Con base en el video puedes observar que para toda $\varepsilon>0$, existe una $\delta>0$, tal que si $f\left(x\right)$ está lo suficientemente cercano a $L$, entonces $x$ está lo suficientemente cercano a $a$, es decir, cuando $f\left(x\right)$ está en el intervalo $\left(L-\varepsilon,\ L+\varepsilon\right)$, $x$ está en el intervalo $\left(a-\delta,\ a+\delta\right)$.
Es claro que la definición intuitiva del límite de una función tiene el inconveniente de qué significa “suficientemente cercano”, sin embargo, en el apartado Definición formal del límite de una función, se presenta la definición formal del límite de una función, considerando las tradicionales letras del alfabeto griego $\varepsilon$ y $\delta$.
Para los propósitos del material, la definición intuitiva del límite es suficiente para determinar el límite de funciones e incluye implícitamente la igualdad de los límites laterales (límites por la izquierda y derecha alrededor de $x=a$. Ahora para ver si te quedó claro el concepto intuitivo del límite de una función se te propone el ejercicio siguiente.
Analiza las funciones mediante la interacción de los recursos GeoGebra para que formules la existencia o no del límite de la función para el valor de la variable que se indica.
a) Analiza con el recurso GeoGebra la función alrededor de $x=6$ y contesta lo que se te pide:
b) Analiza con el recurso GeoGebra la función alrededor de $x=2$ y contesta lo que se te pide:
c) Analiza la función $f(x)$ con el recurso GeoGebra alrededor de $x=-2$ y contesta lo que se te pide:
d) Analiza la función $f(x)$ con el recurso GeoGebra y contesta lo que se te pide:
e) Analiza la función $f(x)$ con el recurso GeoGebra y contesta lo que se te pide:
f) Analiza la función $f(x)$ con el recurso GeoGebra y contesta lo que se te pide:
g) Analiza la función con el recurso GeoGebra y contesta lo que se te pide:
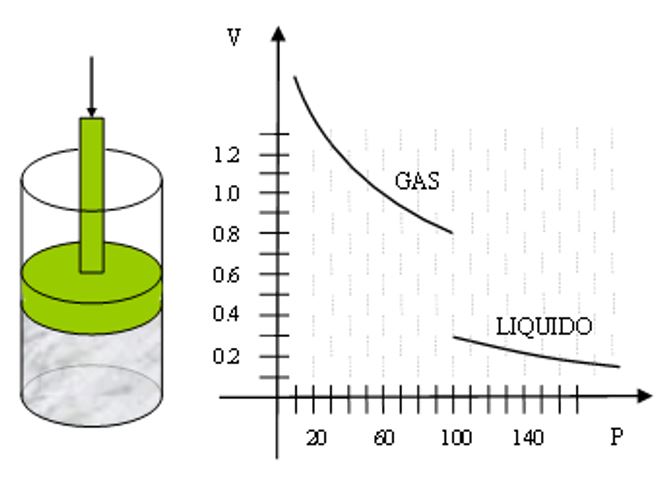
h) Un gas es mantenido a temperatura constante dentro de un cilindro. Si este gas es sometido a cierta presión $P$, su volumen V cambia. Cuando la presión llega a ciertos niveles, el gas se convierte en un líquido. Esta situación queda representada en la gráfica que se muestra a continuación.
